基于客观满意聚类的pH中和过程建模方法

王 娜,胡超芳,师五喜

(1.天津工业大学 a.电气工程与自动化学院;b.电工电能新技术天津市重点实验室,天津 300387; 2.天津大学 a.微光机电系统技术教育部重点实验室;b.电气与自动化工程学院,天津 300072)

0 概述

pH中和过程是具有严重非线性和大滞后的复杂工业过程[1-2],获得性能满意、能够反映其本质特征的模型是对其进行有效控制的重要前提。通常的解决方案有全局建模策略,包括神经网络、支持向量机等,但在处理pH中和这类数据分布离散、幅值变化较大的较强非线性对象时,会因为结构的单一性而难以充分逼近其非线性特性,导致模型的拟合精度和泛化能力较差[3]。

为此,基于分解-合成思想的T-S模糊建模方法[3-5],通过在子空间建立起若干局部线性函数关系的组合来描述全局系统,使规则库得以有效约简,计算复杂性大大降低。

T-S模型的构建通常采用模糊辨识,即模糊子空间的划分来获取规则数、前提参数和后件参数。而规则数对应着模糊子空间的划分,一般采用模糊聚类的方法实现[6-7]。但在实际应用中,模糊聚类的初始参数,即聚类个数和聚类中心通常是事先未知的,一般通过经验或者人为试凑的方式给定,有2类途径:比较法[3,8]或者融合法[3,9-10]。比较法通常采用若干聚类有效性指标的比较确定聚类数,易于受到人为决策的影响;而融合法中不重要聚类的判别和删减过程不仅增加了计算的复杂性,并且容易导致聚类空间出现空洞,使模型的泛化能力变差[9]。此外,由于聚类过程中易受到数据中噪声的影响,可能导致生成的聚类个数过少或者出现冗余,也会直接影响到模糊规则数的确定[11]。

为此,本文提出一种基于客观满意聚类的pH中和过程建模方法。首先改进原始客观聚类分析算法[12-14],其具有对数据中噪声的较强鲁棒性,从而克服噪声对于聚类结果,即聚类个数和聚类中心的影响,可以直接确定一个比较适宜的初始规则数和初始聚类中心,并将其与Gustafson-Kessel(GK)模糊聚类[15-16]相结合,利用GK聚类进一步优化原有的聚类中心及对应的模糊划分。此外,针对建模者对于模型的满意度,在初始模糊划分的基础上,再利用模型的满意度指标进行模糊聚类的迭代,以确定满意的模糊规则数和前提参数,使模型结构更加灵活有效,最后再利用稳态卡尔曼滤波算法[5]估计模型的后件参数,以克服传统最小二乘算法在求解病态矩阵时易导致非数值解的问题,提高计算的稳定性。

1 pH中和过程描述

从系统建模的角度而言,pH中和过程是一个多入多出过程,输入量为酸液流量Fa及所含成分浓度Ca,碱液流量Fb及所含成分浓度Cb,输出量为酸液浓度ωa和碱液的浓度ωb。CSTR的动态模型为:

(1)

(2)

其中,V为反应器的容积。

不失一般性,考虑弱酸强碱过程,其中和滴定方程为:

(3)

其中,wa=[Cl-],wb=[Na+] ,Ka=1.76×10-5为弱酸的电离常数,且pKa=-lgKa。中和滴定曲线如图1所示,可见pH中和值在中和点附近灵敏度很高,而在远离中和点处灵敏度很低。

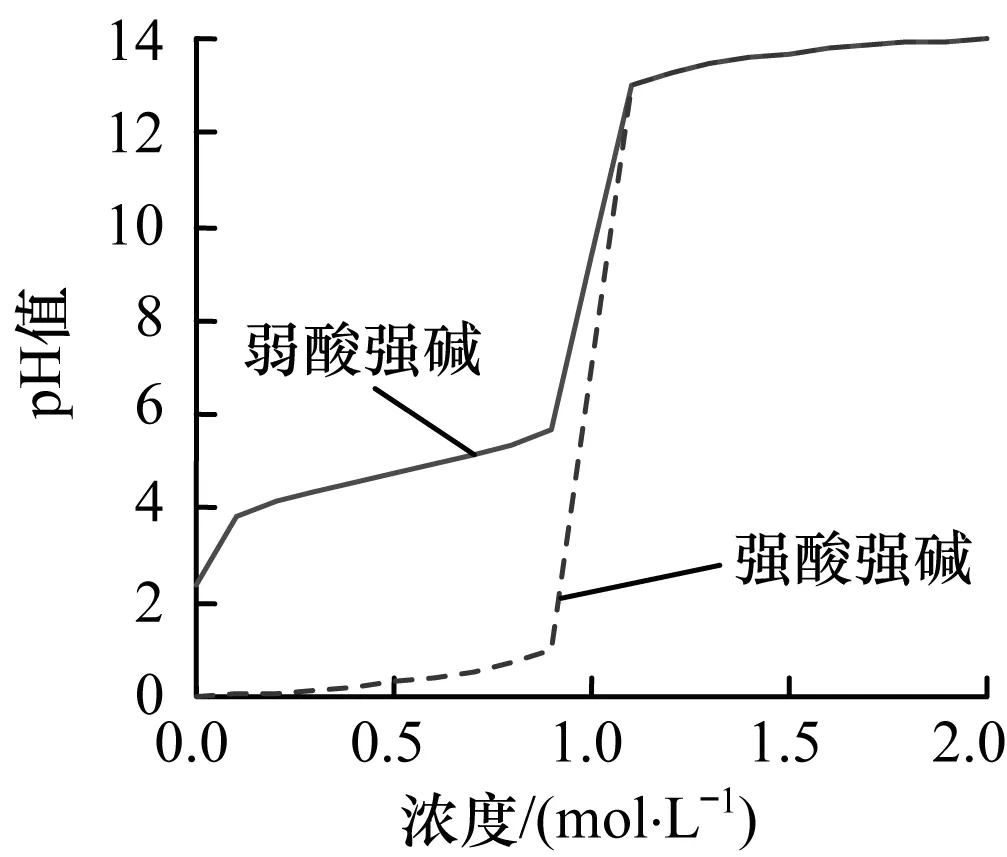
图1 弱酸强碱及强酸强碱中和滴定曲线

2 T-S模糊模型

在非线性系统建模中,T-S模糊模型是一种常用的有效模型结构,规则形式如下[5]:

(4)

采用加权平均法,T-S模型的推理可简化如下:

(5)

3 T-S模型前提参数辨识

3.1 客观满意聚类原理

客观满意聚类首先引入原始的客观聚类算法[12-14]对其进行改进,并将其引入Gustafson-Kessel(GK)聚类[15-16]来提供比较合适的初始聚类个数和聚类中心,以此作为原始输入-输出数据空间的初始模糊划分,并依据用户提供的建模满意度准则,进行后续新的聚类个数生成和聚类中心的更新,以确定最终的模糊划分,其原理如图2所示。

图2 客观满意聚类原理

3.1.1 GK聚类

与传统模糊聚类算法相比,GK聚类利用自适应距离度量取代固定的欧式距离,进行类内距离的计算,从而有效克服了模糊C均值算法易受初始值影响而陷入局部极值的缺点,因而更加适合模糊辨识。

给定数据集Z,GK通过求取目标函数J的极小值来获取给定聚类个数c下的模糊隶属度矩阵U和对应的聚类中心V:

(6)

其中,d(zj,vi)表示样本zj与聚类中心vi之间的距离,受实际的聚类形状影响,并由聚类协方差矩阵Fi决定。

(7)

d2(zj,vi)=(zj-vi)TMi(zj-vi)

(8)

(9)

但GK聚类的初始参数,即聚类个数c和聚类中心V难以确定,常见有比较[3,8]和融合法[3,9-10]。但在如何确定聚类的初始个数上,比较法依赖于聚类有效性指标的相互比较,而融合法采用最大聚类个数开始,依次逐步合并的方式确定最终聚类个数。两者均比较依赖于经验,或者某些假定的数据条件,比如必须满足高斯正态分布等。而对于缺乏先验知识,或者不满足外在假设条件的数据集则缺少有效的提炼聚类个数的方法。并且,还容易受到数据中噪声、数据分布等因素的影响,从而给模型前件参数的确定带来较多的不确定性,进而导致不准确的辨识结果,影响整个模型的精度。为此,提出改进客观聚类算法,并与GK聚类相结合,形成客观满意聚类方法,以改善这一状况。

3.1.2 客观聚类原理

客观聚类的基本原理如图3所示。主要采用相似性数据分级和自组织聚类实现对相似数据子集的共同聚类和比较,其中相似性数据分级利用两两距离最近的数据对排序,以将整个数据集划分为训练集A、B或者测试集C、D,即Z={A,B}or{C,D},并分别在这4个子集上进行自组织聚类, 将各自的聚类结果两两比较以决定最终的聚类结果。

图3 客观聚类的基本原理

为克服原有算法的最近邻聚类效应,导致难于形成较小聚类,以及原有一致性计算中出现的多值解问题,本文采用改进客观聚类算法[14],即引入相对不相似性测度(Relative Dissimilarity Measure,RDM)[17]来确定待融合的聚类,以降低最近邻引起聚类过程的滚雪球问题,提高算法的准确性,并提出改进一致性准则来克服多值解的收敛问题,提高求解的稳定性。

与传统硬聚类相比,改进客观聚类的特点主要为:

1)相似性数据分级

通过相似性分级,原始的数据集Z被重新划分为2组数据子集{A,B}或者{C,D}。相比之下,子集A与B的相似度最高,而C与D亦然。并且,{A,B}的相似度高于{C,D},因此将{A,B}作为内部训练集进行聚类,来获得原始数据集Z的一种可能的聚类结果,而{C,D}作为测试集来校验{A,B}结果的准确性,为最终的聚类结果的确定提供外部依据,因此,在内外2种准则的共同检验下,最终聚类结果的有效性得以保证。

图4 训练子集A、B的偶极子构成

2)启发式自组织聚类

不同于传统的层次聚类,启发式自组织聚类利用一种新定义的距离测度-相对不相似性测度(RDM)来衡量[17]每次聚类中待融合的2个聚类i和j之间的相似性,并且还考虑了未被合并的聚类k对于本次聚类合并的影响,对于数据的分布更具有较强鲁棒性。

(10)

(11)

改进一致性准则定义如下:

(12)

与原始的一致性准则相比,改进的一致性计算采用同一位置下不同子集的聚类中心之间的差异来代替数据点之间的差值,从而降低了数据中噪声点对一致性计算的影响,确保了聚类结果的准确性。

3.2 基于客观满意聚类的T-S模型前提参数辨识

4 基于客观满意聚类的T-S模糊辨识

如2.3节所述,利用所提的客观满意聚类算法的聚类结果可以确定T-S模型的初始结构,规则数即为聚类个数,模糊划分矩阵中的隶属度元素即为所对应规则的前提参数,但这一结果并非模糊模型的最优结构。其主要原因在于聚类算法在使用数据建模时,主要利用聚类的相似性原理,以寻找最优的聚类为目的,而建模对象之间的输入-输出关系的某些非线性特性就可能被忽视,造成欠拟合,所以最终的聚类结果可能并不能满足建模精度要求。

如图5所示,在非线性曲线中,曲线l1和l2段的动态特性仅用聚类C1来表示,l4和l5段仅用聚类C3所覆盖,显然建模的拟合精度不足。VS表示非常小,S表示小,M表示中,L表示大,VL表示非常大。为此,在客观满意聚类基础上,引入一种误差反馈机制,利用聚类后模型与实际数据输出之间的最大误差来反馈所建模型的拟合效果,并以此为聚类是否继续迭代的依据,直至模型与数据输出之间的误差降低至某一允许的精度范围内终止。在此前提参数的辨识基础上,利用稳态卡尔曼滤波算法[5]估计规则的后件参数,完成整个T-S模糊模型的结构和参数辨识。

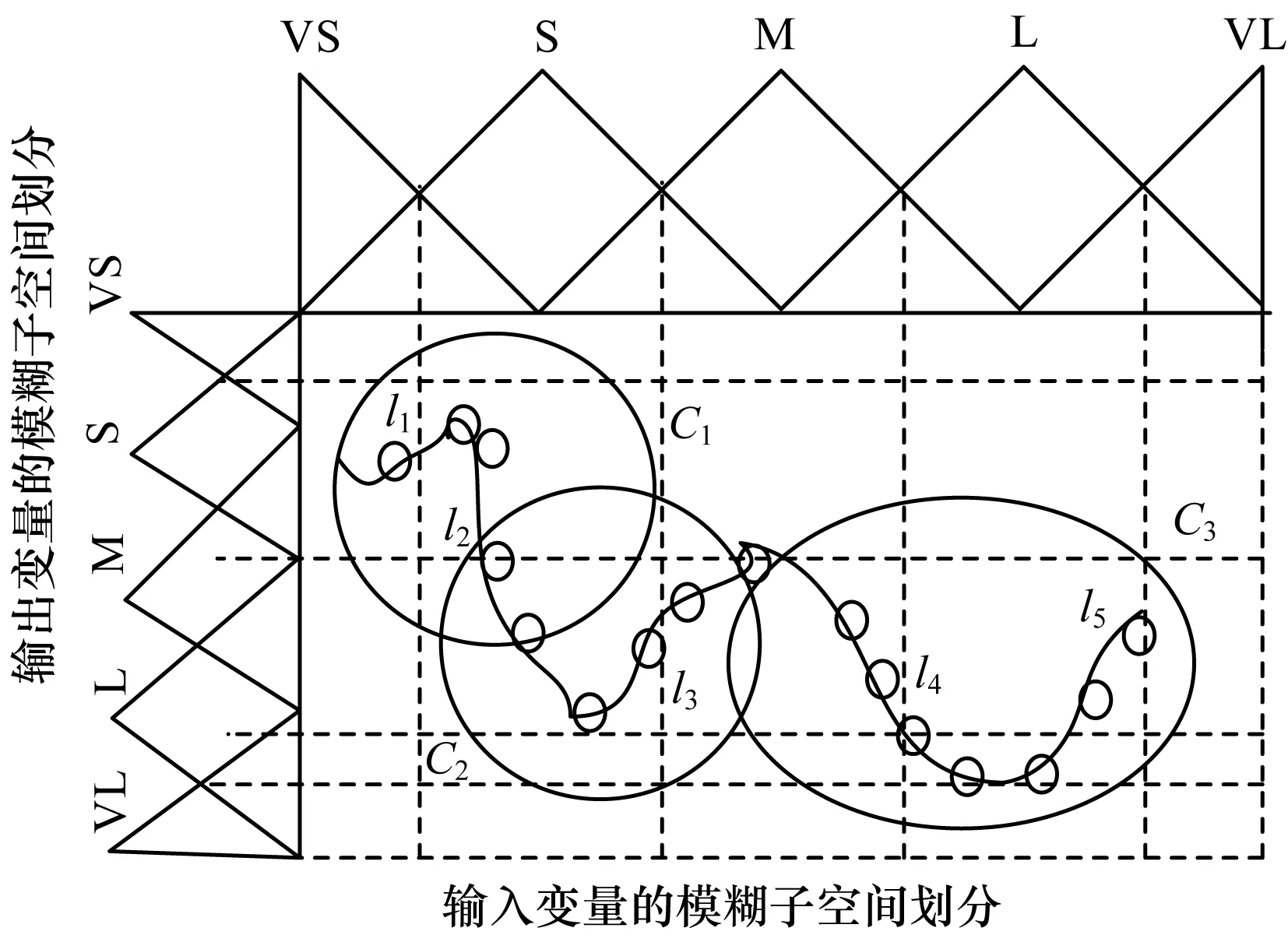
图5 模糊聚类划分的欠拟合

算法步骤归纳如下:

步骤1采用EOCA 算法确定一个初始聚类结果{c0,V0},c0为聚类个数,V0为初始聚类中心集。

5 仿真研究

考虑式(1)～式(3)描述的弱酸强碱中和过程,给定酸液流量Fa,则系统输入输出分别为碱液流量Fb和流出物的pH值。样本集(Fb,ypH)可通过机理模型式(1)～式(3)得到。在Fb中加入[-51.5,+51.5]范围内的变化量,由此产生300组样本。假设T-S模型包含2个输入量,其表达式为:

(13)

图6 一致性准则与聚类个数关系曲线

给定初始规则数n=c=2 ,初始聚类中心Vi,采用GK和稳态卡尔曼滤波法分别辨识前提参数和结论参数之后,得到第i条规则Ri为:

(14)

图7 无噪声下实际系统输出与模型估计的误差曲面

最终产生的5个聚类中心在整个数据集中的分布如图8所示。

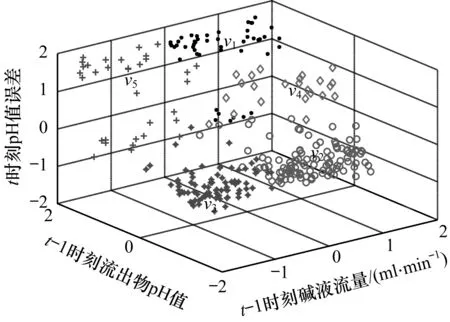
图8 无噪声下c=5时的聚类子集与聚类中心分布

由图8可见,整个数据集被均匀划分为5个聚类,每个聚类中心即为模糊规则的中心,数据与聚类中心之间的模糊隶属度矩阵决定了其前提参数。以第1个数据为例,其在模糊矩阵中表示为:U_c5(1,:)=[0.03 0.79 0.06 0.09 0.02],以其最大的隶属度值0.79应该归为第2类,其余数据以此类推,形成上述5个聚类子集{c1,c2,c3,c4,c5},对应聚类中心{v1,v2,v3,v4,v5}。系统输出与模型输出的比较曲线如图9所示。

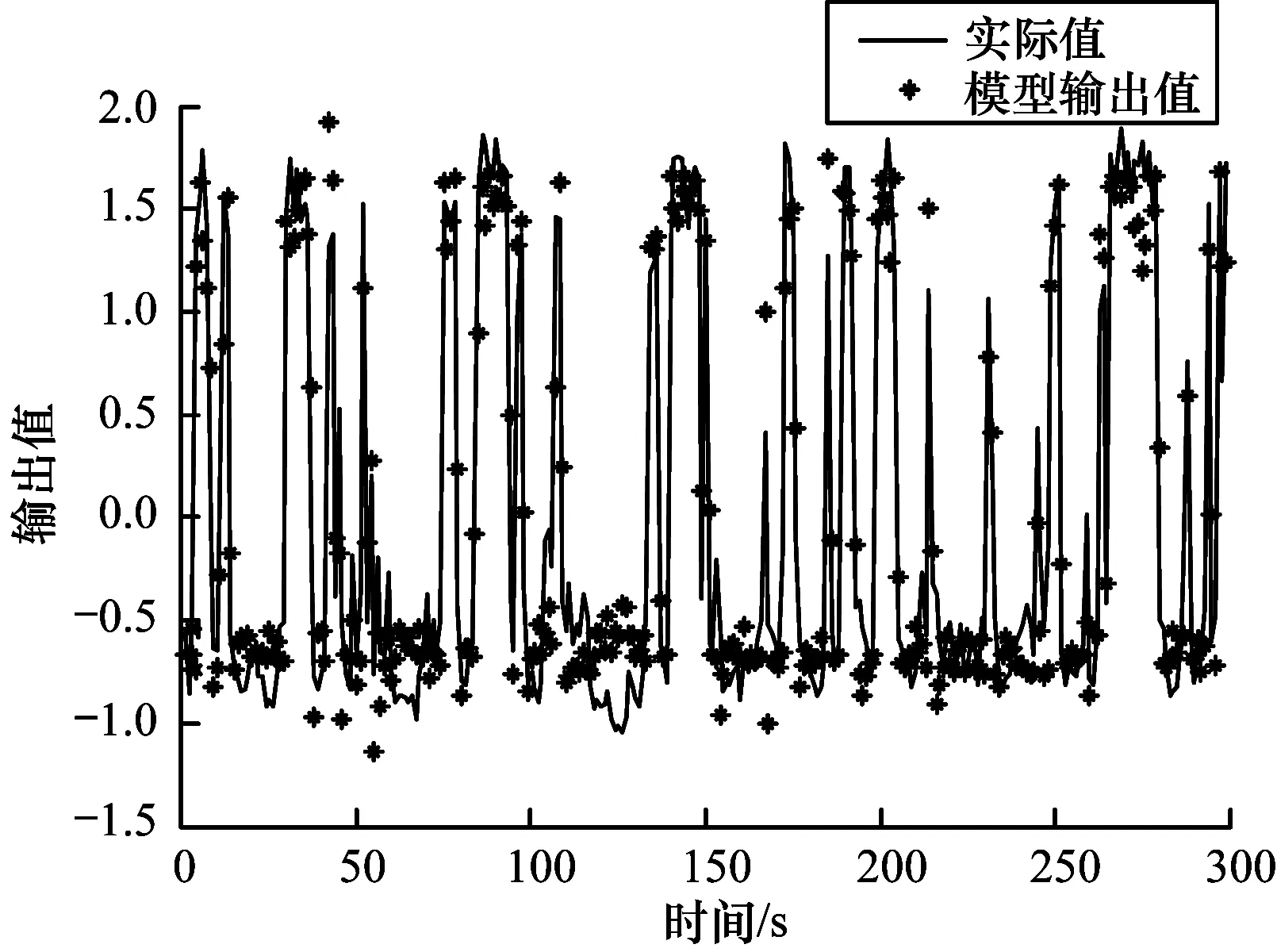
图9 无噪声下系统实际输出与模型输出的误差比较曲线

上述结果为未添加噪声下的模型,为验证所建模型的鲁棒性,对上述数据的输入和输出同时添加信噪比为5 dB的白高斯噪声,采用同样方法训练,结果得到(itaCD=0.003 3)c=2∠(itaAB=1.183 2)c=6,故选取初始聚类个数为2。经过GK模糊聚类和迭代,以及稳态卡尔曼滤波后,得到聚类个数为4时MSE为0.64,而聚类个数为5时MSE为0.65,误差精度变化不大,故确定最终规则数为4,MSE为0.64,如图10所示。

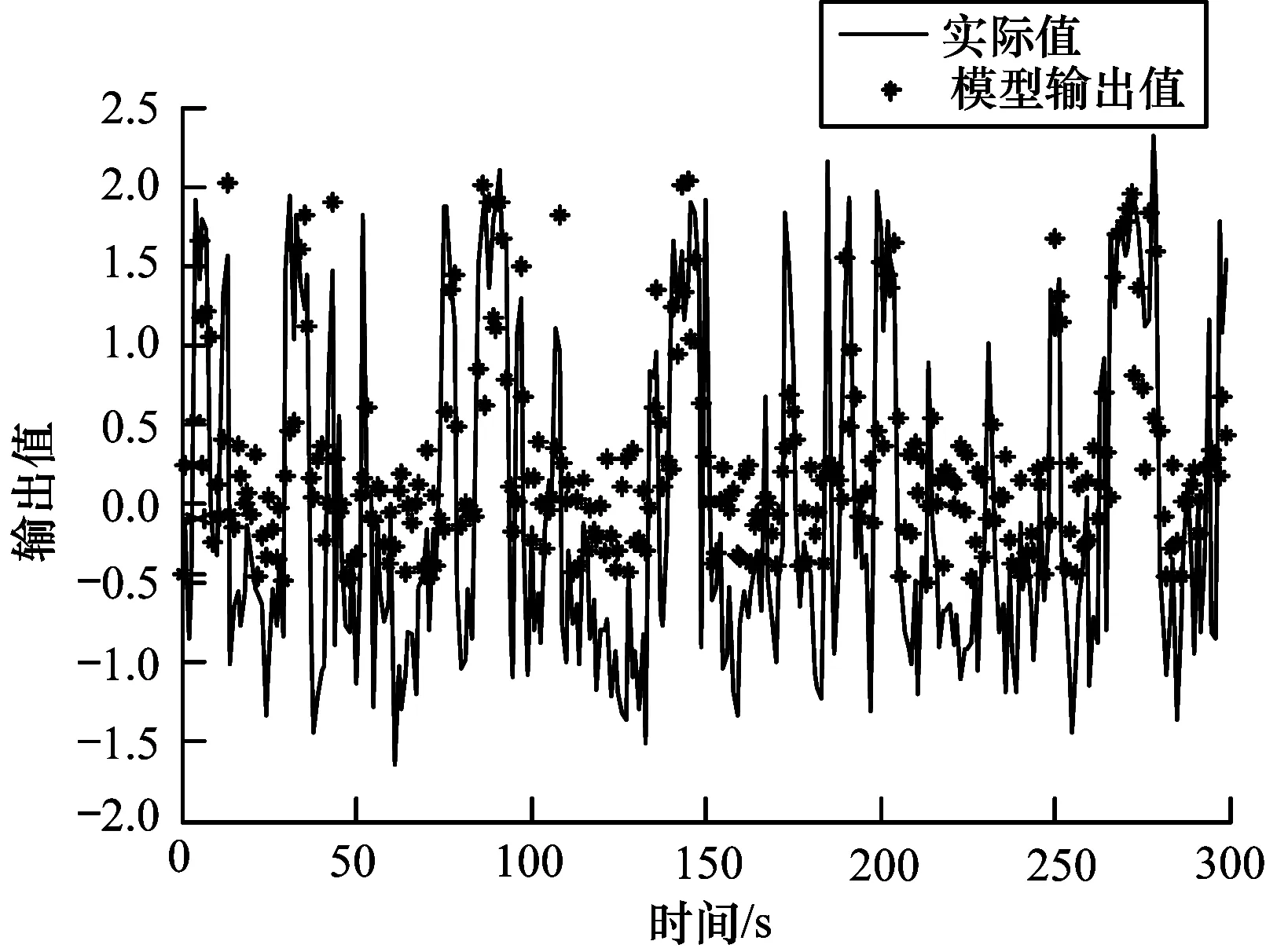
图10 有噪声下系统实际输出与模型输出的误差比较曲线

无噪声环境下,采用上述训练数据集,所提方法与其他模糊聚类建模效果比较如表1所示。由表1可见,与USOCPN相比,本文方法规则数较少,并且训练精度处于同一量纲内,因此具有更加精简的模型结构,其结构和参数辨识的计算效率相应就得以大大降低。与GK模糊聚类相比,本文方法取规则数为5时,其建模精度处于同一量纲范围内,但其初始聚类个数和初始聚类中心均可由客观聚类方法直接一次给定,避免了GK模糊聚类中初始聚类参数难以确定,采用试凑而带来的不确定性,更加直接有效。并且,在添加噪声之后,与GK模糊聚类相比,模型的拟合精度处于同一量级范围内,但却避免了GK模糊聚类难以确定模糊规则数的缺点,使得初始结构的确定更加准确。同时,能够以较少的规则数获得较为满意的建模精度。

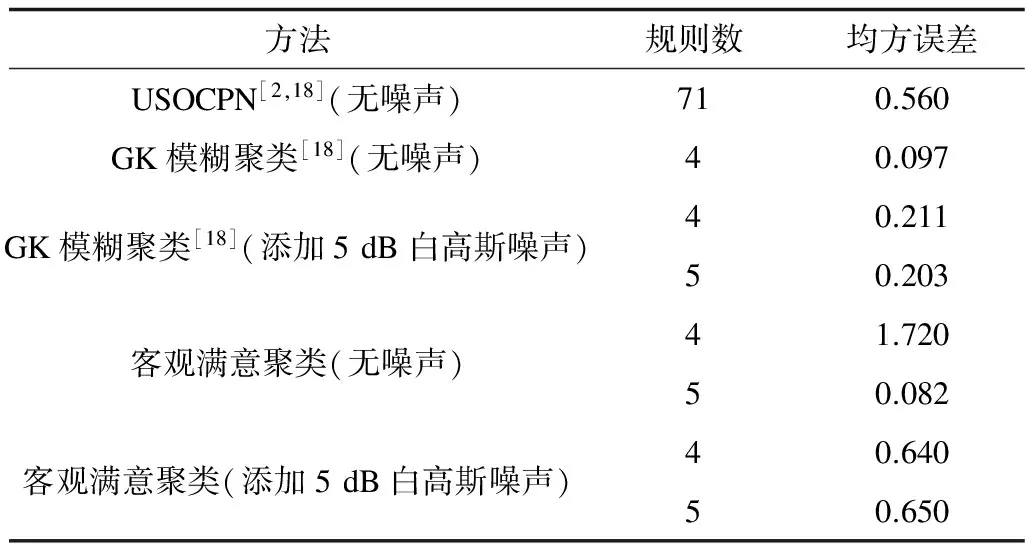
表1 客观满意聚类与其他模糊聚类的建模性能比较

6 结束语

本文利用客观模糊聚类辨识pH中和过程,提供了一种新型的T-S模糊建模方法。该方法能从系统的实际输入输出数据出发,自适应地快速确定系统的模糊规则数、前提参数和后件参数。对pH过程的仿真研究验证了所建模型对系统具有较强的拟合能力,并且对于噪声数据的拟合有较强的鲁棒性,结构简单,易于实现。

[1] BUCHHOLT F,KUMMEL M.Self-tuning Control of a pH Neutralization Process[J].Automatica,1979,15(6):665-671.

[2] NIE Junhong,LOH A P,HANG C C.Modeling pH Neutralization Processes Using Fuzzy-neural Approaches[J].Fuzzy Sets and Systems,1996,78(1):5-22.

[3] 李 柠,李少远,席裕庚.利用模糊满意聚类建立pH中和过程模型[J].控制与决策,2002,17(2):143-147.

[4] 李香娜.基于T-S模糊模型的酸碱中和过程的系统辨识[J].华北科技学院学报,2010,7(3):56-60.

[5] TAKAGI T,SUGENO M.Fuzzy Identification of Systems and Applications to Modeling and Control[J].IEEE Transactions on Systems,Man,and Cybernetics,1985,15(1):116-132.

[6] YI Yang,FAN Xiangxiang,ZHANG Tianping.Anti-disturbance Tracking Control for Systems with Nonlinear Disturbances Using T-S Fuzzy Modeling[J].Neurocomputing,2016,171(3):1027-1037.

[7] 宋 俐,谢 刚,杨云云.基于模糊聚类的社团划分算法[J].计算机工程,2016,42(8):126-133.

[8] QIAO Junfei,LI Wei,ZENG Xiaojun.Identification of Fuzzy Neural Networks by Forward Recursive Input-output Clustering and Accurate Similarity Analysis[J].Applied Soft Computing,2016,49:524-543.

[9] KRISHNAPURAM R,FREG C P.Fitting an Unknown Number of Lines and Planes to Image Data Through Compatible Cluster Merging[J].Pattern Recognition,1992,25(4):385-400.

[10] KAYMAK U,BABUSKA R.Compatible Cluster Merging for Fuzzy Modeling[C]//Proceedings of IEEE International Conference on Fuzzy System.Washington D.C.,USA:IEEE Press,1995:897-904.

[11] 刘士荣,余建军,林卫星,等.启发式模糊聚类学习在函数逼近和非线性系统建模中的应用[J].模式识别与人工智能,2003,16(2):230-235.

[12] 王 娜.基于客观聚类的模糊建模方法研究[D].上海:上海交通大学,2009.

[13] 贺昌政.自组织数据挖掘与经济预测[M].北京:科学出版社,2005.

[14] 王 娜,杨煜普.一种基于改进客观聚类分析的模糊辨识方法[J].控制与决策,2009,24(1):13-17,22.

[15] QIU Haobo,XU Yanjiao,GAO Liang,et al.Multi-stage Design Space Reduction and Metamodeling Optimization Method Based on Self-organizing Maps and Fuzzy Clustering[J].Expert Systems with Applications,2016,46(3):180-195.

[16] GUSTAFSON D,KESSEL W C.Fuzzy Clustering with a Fuzzy Covariance Matrix[C]//Proceedings of IEEE Conference on Decision & Control.Washington D.C.,USA:IEEE Press,1979:761-766.

[17] MOLLINEDA R A,ENRIQUE V.A Relative Approach to Hierarchical Clustering[M].Amsterdam,the Netherlands:IOS Press,2000:19-28.

[18] 李 柠.多模型建模与控制的若干问题研究[D].上海:上海交通大学,2002.