某舰炮伺服系统建模仿真

王丹峰，申中华

（中船重工第七一三研究所，河南 郑州 450015）

0 引言

某舰炮伺服控制系统采用典型的三环回路控制结构，即：位置环、速度环、电流环。计算机作为位置环控制器核心，对整个伺服控制系统以及舰炮整体采取集中监控、离散控制。位置环控制器算法由计算机程序实现，其核心是一段分段离散PID控制语句。速度环和电流环分别集成在伺服驱动器内部，速度环和电流环都采用了PI控制器。舰炮伺服系统的控制精度可以从两方面提高，一是选用更高精度的伺服驱动器以及执行机构，二是通过改进位置环控制器算法。因此为了研究控制器算法，建立被控对象的仿真模型非常必要，文献[5]建立了直流无刷电机伺服系统的速度环和电流环，并没有对位置环进行研究，不能实现定角度运行。文献[6，7]对无刷直流电机的数学模型进行了深入研究，分析了产生脉动的数学机理，并且给出了一些可行性改进措施。本文根据实际物理模型，旨在建立与实际舰炮伺服系统相一致的仿真模型。建立逼近的仿真模型对于研究位置环控制算法具有重要意义。

1 三环回路BLCDM数学模型

根据文献[1，4]，无刷直流电机动态结构框为图1中虚线框，据此构建了数学模型下的三环回路控制系统，结构原理如图1所示。

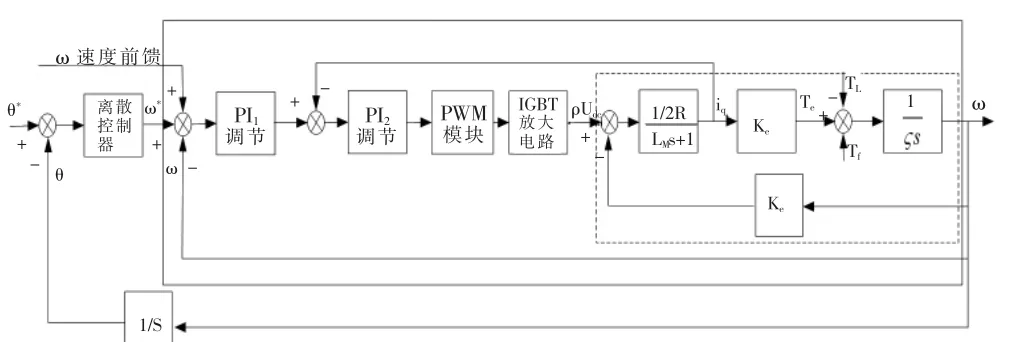
图1 三环回路控制原理框图Fig.1 Three loop control schematic diagram

其中小虚线框部分为电机控制对象，大实线框是电流环和速度环，为了简化控制系统数学模型，图中省略了速度反馈检测装置和位置环检测装置，认为反馈系数为1，忽略检测装置的延迟，认为检测信号瞬时完成，这样简化并不影响我们后面的数学分析。

速度和电流控制器均采用PI控制器，PI控制器的数学模型 Kp+Ki/s；PWM 和 IGBT 数学模型为 Kc/（Tcs+1），其中Tc为PWM控制器的平均失控时间，Tc根据PWM调制频率而定Tc=1/f，Kc为控制器功率放大系数。

带入各部分传递函数，可以得到系统正向控制闭环传递函数：

可以看出系统是5阶线性系统，PI控制器的参数可以通过计算获得想要的性能参数[4]，这里我们将系统调节成3阶线性系统，通过调节PI参数，获得相应极点位置，来达到系统满意的响应指标。

根据控制目标，做了以下假设：

（1）PI2控制器的参数与电机大惯性环节参数相等，分子分母零极点对消，即：

（2）同时认为PWM环节动态响应很快，忽略PWM模型时滞的影响，将伺服控制器数学模型简化成比例环节，即（Tcs+1）=1，这时系统模型简化为：

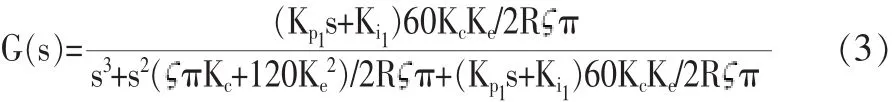
根据原理图搭建数学仿真模型，其中伺服驱动器放大系数根据经验取值25，电枢漏磁时间常数Lm=0.0005，负载转矩20Nm，在Matlab工具箱帮助下，通过参数调节Kp1=12，Ki1=0.01（积分系数也可以等于零，此时系统变成二阶系统）仿真结果如图2所示，从图2中看出，数学模型下系统响应很快，系统到达最高转速几乎没有超调，实际物理伺服系统的加速度并做不到这么大，仿真结果无法逼近实际的运行状态，再加上物理系统存在库伦摩擦、控制器饱和等非线性因素，导致了数学模型在实际工程中无法应用，因此有必要建立更加接近物理系统的仿真模型。

图2 数学模型调转60°速度响应曲线Fig.2 Mathematical model steps 60°response curve

2 基于SIMPOWER工具箱建立的伺服系统仿真模型[2 ]

根据原理图1，利用Matlab的SIMPOWER工具箱搭建控制系统仿真模型，该模型包含了IGBT驱动电路、电机模型、霍尔信号检测，PWM发生环节等。其中电机模型采用了工具箱自带的模块。以下主要针对速度环，电流环进行分析。

速度环是将给定转速与反馈转速做比较，给出误差信号，经过PI控制器，转换成相应的转矩输出，给电流控制器，其中对转速和PI控制器都进行了饱和限制，模拟实际系统的最高转速饱和，如图3所示。

图3 速度控制器仿真模型Fig.3 Velocity controller simulation model

电流控制器设计：电流给定与霍尔信号逻辑处理模块的输出相乘，得到给定期望电流，之后与反馈电流相减，差值信号经过PI控制器输出给PWM发生器，控制占空比，PWM发生器输出PWM波驱动桥臂上的IGBT。电流环控制器结构总图如图4所示。

图4 电流控制器仿真模型结构总图Fig.4 Current controller simulation model

霍尔信号处理模块：对于三相电机，需要配备三个霍尔传感器来检测转子相对电枢位置，霍尔传感器根据检测到的开关信号，经过逻辑处理，转化成导通桥臂的逻辑信号，检测位置与相序关系如表1所示，模块原理图如图5所示。

表1 霍尔传感器信号输入输出编码表Tab.1 Hallelement input&output signalcoding

图5 decoder霍尔信号逻辑处理模块Fig.5 Hall signal logical process model

电流比较环节完成了给定电流和反馈电流的差，然后将电流差值送入电流PI控制器，PI控制器输出送给PWM发生器，产生的PWM波驱动IGBT，如图6、7所示。

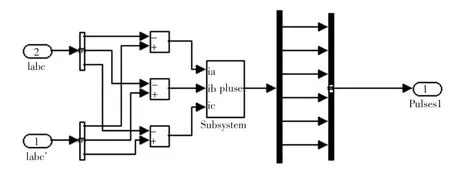
图6 电流比较环节Fig.6 Current compare block

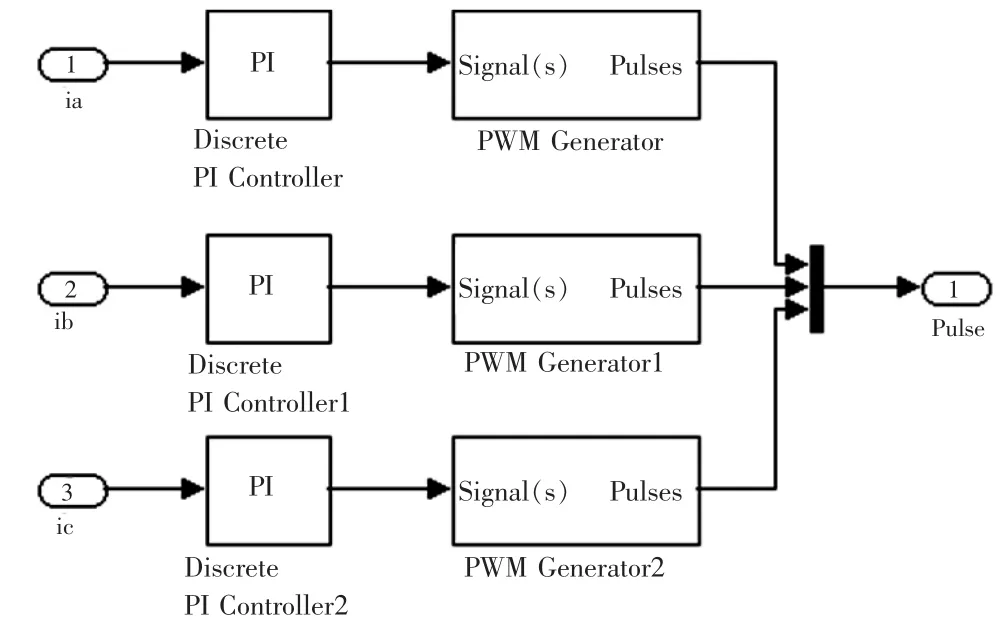
图7 电流PI调节和PWM发生环节Fig.7 Current PI controller and PWM generator block

位置环控制器是由S-function模块实现，模块功能是将给定位置和反馈位置实时比较，经过非线性分段PID处理，输出相对应的转速控制信号，模块程序流程图如图8所示。

为了构建实际系统的仿真模型，保证与实际系统相匹配，电机部分参数测量获得，单相电阻R=0.05Ω，电机铭牌标示额定转速3000r/min，电机额定输入电压AC165V，实际测量直流母线测端电压255V，启动最大电流155A，额定输出转矩30Nm，静转矩75Nm（最大值），最大转矩200Nm，电机轴转动惯量 Ge=0.0454kg·m2。

本文只针对舰炮高低系统做仿真，由于实际高低系统通过齿轮啮合将力矩传送给高低，在设计位置环控制器的时候将减速比计算在内，仿真显示速度和误差都是按照舰炮高低实际运行的速度来显示，保持与舰炮监控台的一致的速度显示效果，经过模型参数设置、PID参数调试，仿真结果如下：

等速 60°/s 转动60°，速度、误差响应曲线如图9所示。

正弦运动，振幅25°，周期 3.75s，速度、误差响应曲线如图10所示。

图8 位置环控制器程序流程图Fig.8 Position loop controller program flow chart

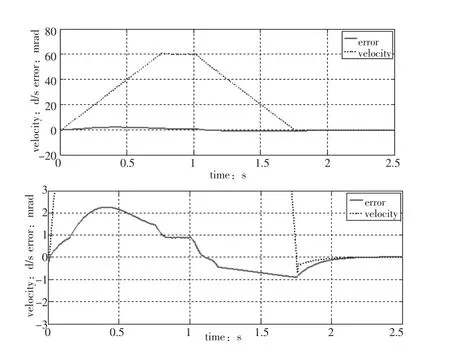
图9 等速60°/s转动60°速度、误差响应曲线Fig.9 Constant speed 60°/s rotate 60°velocity error response curve

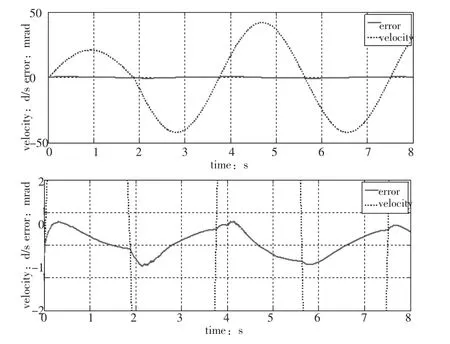
图10 正弦运动，周期3.75s、幅度25°速度、误差响应曲线Fig.10 Sinusoidal motion Cycle 3.75s Amplitude 25°velocity error response curve

从等速60°/s误差曲线可以看出，加速、减速阶段误差比较大，达到2mrad左右。当运行时间大于等于2s的时候，速度经过位置环控制器调整，误差减小，达到了0.1mrad，基本保持了与实际伺服系统一致的运行结果。

从正弦运动误差曲线看出，误差保持在正负0.8mrad范围内，与实际物理伺服系统保持一致。

3 结论

仿真模型能够实现调转、等速、正弦运动三种基本运动形式，仿真的速度、误差曲线与实际物理系统基本一致，所建立的仿真模型很好的模拟了实际物理系统，能为分析和设计位置环控制器提供帮助。

[1]张琛.直流无刷电机原理及应用[M].上海：机械工业出版社，1995.

[2]洪乃刚.电力电子、电机控制系统的建模与仿真[M].北京：机械工业出版社，2010.

[3]叶金虎.现代无刷直流永磁电动机的原理和设计[M].北京：科学出版社，2007.

[4]陈伯时.电力拖动自动控制系统（第三版）[M].北京：机械工业出版社，1992.

[5]杨向宇，杨进，邹利平.直流无刷电机控制系统的建模与仿真[J].华南理工大学学报，2005，8.

[6]许镇琳，柔建平，王秀芝.永磁式BLCDM交流伺服系统转矩脉动最小化[J].天津大学学报，1994，4.

[7]许镇琳，吴忠，王秀芝，江伟.无刷直流伺服电机换向最优控制[J].自动化学报，1996，4.