基于自由度变动的平面要素尺寸公差数学模型

邱义臻,熊 焰,刘方方

（宿迁学院 机电工程系，江苏 宿迁 223800）

0 引言

实现CAD/CAM有效集成，有利于缩短产品设计周期，降低产品的成本，提高产品的质量和性能，增强市场竞争力与提升市场份额。在目前CAD软件系统中，其核心是一个实体造型器，名义几何信息能够得到很好表达，而变动几何信息（如公差信息）却是以文本/注解的形式存储在计算机中，不能用于计算机辅助公差分析与综合，这阻碍了产品设计的自动化，成为CAD/CAM有效集成的瓶颈[1]，因此，公差信息是CAD/CAM有效集成中必需的信息之一。在计算机中表示公差信息，就是在计算机中对某一实体模型或特征模型进行准确无误的公差表述，一是公差信息以一种数据结构形式存在（包含于现有的CAD系统中）；二是用数学的方法描述与解释公差信息，必须与公差标准（产品几何规范标准体系GPS）一致，要求完整、有效、准确。建立公差数学模型，对CAD系统中包含公差信息的语义作出正确的解释，从而使之在CAD/CAM集成中发挥重要作用。基于自由度变动的平面要素尺寸公差数学模型研究，以现行国家标准和公差的数学定义为基础，给出平面要素基于自由度变动的数学表示方法，并对尺寸公差进行数学定义，建立基于自由度变动的平面要素尺寸公差变动数学模型。

1 平面要素的自由度

机械零件是由构成其几何特征的若干点、线、面构成的，这些统称为几何要素[2]。机械零件几何要素也具有类似刚体的自由度特性，但与刚体的自由度不同的是几何要素存在恒定度[3]，即自由度数量少于6个（F=6-n，式中：n是恒定度），所谓恒定度就是几何要素沿某方向运动（平动或转动）时不产生新的实体。平面要素具有3个自由度，法线方向的1个平移自由度和平面内的2个转动自由度，如图1所示，沿Z坐标轴方向的平移自由度Tz和绕X、Y坐标轴的转动自由度 Rx、Ry。

图1 平面的自由度

2 平面要素基于自由度变动的数学表示

2.1 公差坐标系的建立

公差坐标系用来确定平面要素自由度方向，表示平面要素相对于公称位置在方向、位置上的变动情况。如图2所示，坐标系应建立在平面要素的公称位置上，公差坐标系的原点与平面要素的中心重合，Z轴为平面要素的固有方向，即同向自由度方向（法向），表示平移自由度，X轴和Y轴分别表示2个转动自由度。

2.2 平面要素基于自由度变动的数学表示

在平面要素3个自由度Z、α、β方面分别给定一变动dz、dα、dβ，如图 2 所示，则其的变动方程为：

写成平面要素的一般表示形式：

式中：A=dβ，B=dα，C=-1，D=dz

其公称平面要素的方程为：

根据式（1）～（3）可知，平面要素的数学方程可以通过其自由度变动来表示，即只要给出其自由度变动，就反映出平面要素的变动情况，因此，可以将其自由度变动定义为模型的设计变量。

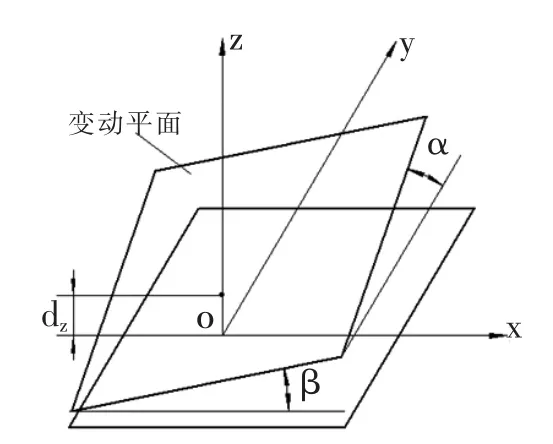
图2 坐标系及平面几何要素的变动形式

3 平面要素的尺寸公差数学模型

机械零件上平面要素的公差是控制平面要素在尺寸、形状、方向及位置上偏离理想状态的程度，因此，建立平面要素的尺寸公差数学模型，就是数学的方式来描述和解释公差信息中成员的含义，一是平面要素公差域（公差域是指允许尺寸、形状和位置变动的区域，在几何上表现为两个相距为公差值大小t的两平行平面之间的区域）的形成与表示；二是变动后平面要素的形成与表示。如图3所示，用任意位置平面说明公差域及变动后平面要素的形成与表示。

3.1 平面要素尺寸公差域边界的数学模型

图3 确定任意位置平面的组成要素的尺寸及公差

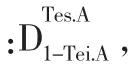
图4 公差坐标系

如图4所示，在该坐标系中，平面的组成要素A点、B点、C点的坐标分别为：

其中：

如图4所示，在该坐标系中，平面尺寸公差域上限平面组成要素As点、Bs点、Cs点的坐标分别为：

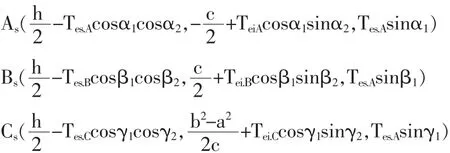
上式中 α1、β1、γ1分别为点 A、B、C 处所加公差约束的方向，α2、β2、γ2分别为点 A、B、C 处所加公差约束方向在xoy平面上的投影与x轴的夹角。由于Tes.A、Tes.B、Tes.C要远远小于 a、b、c，故 As、Bs、Cs的坐标可简化为：

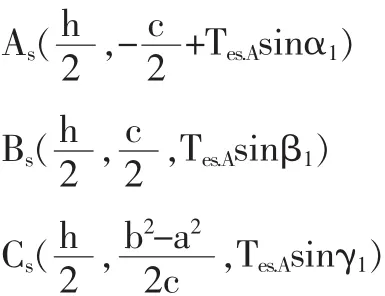
故平面要素尺寸公差域上限平面的方程为：

其中：

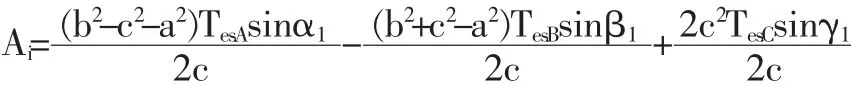
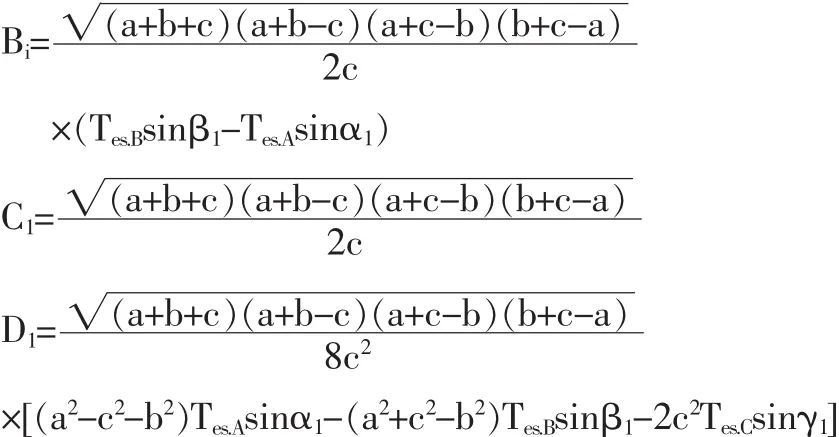
因此，可以得出平面要素公差域上限平面的模型变量为：

同理，可求出平面要素公差域下限平面的模型变量为：

3.2 变动平面的数学模型

平面要素的公差域为两个相距为公差值大小t的两平行平面之间的区域。显然，在求出了的尺寸公差域边界的数学模型之后，即确定了变动平面的变动范围。

因此，对变动平面模型变量的约束范围，即为平面要素公差域的上下边界（上边界zmin、下边界zmax）。具体表示为：

变动平面的约束范围为：

式中：z0=min｜｜zmin，zmax｜｜；z1和 z2分别为尺寸公差域的下边界和上边界。

用任意位置平面说明建立平面要素的尺寸公差数学模型，解释公差信息中每一个成员的含义，具有一定普遍性和通用性。

4 结论

基于自由度变动的平面要素尺寸公差数学模型的建立，以自由度变动作为平面要素尺寸公差模型变量，用任意位置的平面要素分析了平面要素尺寸公差数学模型的公差域边界、变动要素的模型变量，完整准确地表示出尺寸公差的语义，这对于CAD/CAM集成有着十分重要的意义。

[1]张马彪，叶晓平，刘玉生，等.基于自由度变动的直线尺寸公差数学模型[J].工程设计学报，2009，6.

[2]甘永立.几何量公差与检测[M].上海：上海科学技术出版社，2010.

[3]吴玉光，张根源.基于几何要素控制点变动的公差数学模型[J].机械工程学报，2013，3：138～146.