基于第三方软件建立射波刀蒙特卡罗模型的研究*

朴俊杰 徐寿平 段学章 曲宝林 徐慧军 孙 静 王 佳 丁俊强 王东方

蒙特卡罗算法(Monte Carlo Methods)[1]又称随机抽样技巧或统计试验方法，模拟了所有光子在其入射路径上的能量沉积，并且考虑了非均匀介质的散射所带来的影响，在放射剂量运算方面成为金标准，得到了世界各国专家和组织的认可[2]。

射波刀[3](CyberKnife)系统是全身立体定向手术平台，由美国斯坦福大学Adler[4]教授研发，主要由机器人机械臂、影像定位系统、同步呼吸追踪系统、加速器、准直器更换系统、治疗床和机电配套系统共7个部分组成[5]。其中机械臂前端配置了一个能量为6 MV、剂量率为800 MU/min的X射线直线加速器，可从1900多个不同方位实现射束的非共面照射[6]。加速器前端可以使用12个大小不同孔径的准直器，其孔径从小至大依次为5 mm、7.5 mm、10 mm、12.5 mm、15 mm、20 mm、25 mm、30 mm、35 mm、40 mm、50 mm和60 mm，针对不同位置和大小的肿瘤可选取相应尺寸的准直器来设计计划[7]。

为了更好地研究CyberKnife系统的射线特性，尤其是在非标准条件下的小野剂量标定与校准，本研究基于蒙特卡罗工具BEAMnrc[8]模拟CyberKnife治疗头的输运过程(包括电子束打靶之前)，得到一个精确的CyberKnife治疗头的蒙特卡罗模型，为后续研究提供工具和参考。

1 材料与方法

1.1 材料

本研究所模拟CyberKnife为解放军第302医院肿瘤放射治疗中心所使用的G4版本，所有元器件物理尺寸均根据Accuray公司提供的数据，所使用束流特性数据(百分深度剂量、离轴比、输出因子、射线质以及修正因子)均以三维水箱实际测量为准，三维水箱采用PTW MP3-M治疗射束分析仪，探头为PTW 60017 Dosimetry Diode E(如图1所示)。

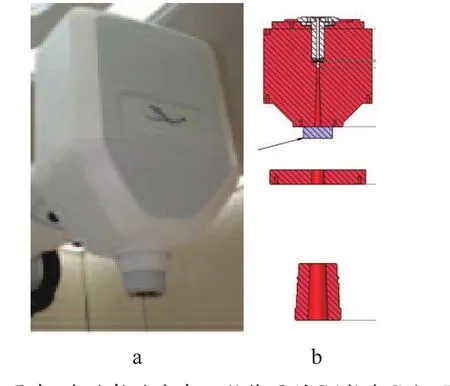
图1 CyberKnife治疗头示意图

其中，百分深度剂量(percent depth dose，PDD)参考条件为源皮距(source skin distance，SSD)=80 cm；离轴比(off axial ratio，OAR)参考条件为源轴距(source axial distance，SAD)=80 cm，扫描深度为1.5 cm、5 cm、10 cm、20 cm及30 cm；输出因子(OF)参考条件为SAD=80 cm，深度为1.5 cm；射线质(Q)参考条件为SAD=100 cm、60 mm准直器，分别取水下深度为d1=10 cm和d2=20 cm的读数，组织模体比(tissue phantom ratio，TPR)20/10=TPR20/TPR10。

1.2 方法

本研究采用BEAMnrc[9]与DOSXYZnrc[10]蒙特卡罗程序，两个程序建立在电子光子簇射(electron gamma shower，EGS)模拟基础上，是由加拿大国家研究委员会(National Research Council Canada，NRCC)开发出来专门用于模拟光子、电子的输运过程的蒙特卡罗程序，提供了多达25种元件模块及16种粒子源类型，是应用广泛且准确的蒙特卡罗程序。

(1)CyberKnife模型的建立。CyberKnife模型分为两部分：①利用BEAMnrc建立CyberKnife的物理机械结构模型，设置电子束束流参数，得到相应的相空间文件；②利用DOSXYZnrc建立水模体模型，引用前面生成的相空间文件，得到水模体中的剂量场分布，将模拟得到的数据与实测数据对比，根据结果，调整电子束束流参数，直到模拟数据与实测数据一致(如图2所示，见表1)。

(2)确定电子束束流参数。确定电子束束流参数方法：①调整平均能量(Ē)，使PDD曲线的模拟值与实测数据相一致，即全局＞90%以上的点误差＜2%；②固定Ē，调整强度分布半高宽(full width at half maximum，FWHM)，使OAR的模拟值与实测数据相一致，全局＞90%的点误差＜2%；③当所模拟PDD和OAR都与实测数据一致时，方可认定所建立CyberKnife模型能够代表实际射线的输运过程。

图2 CyberKnife的物理机械结构模型预览图

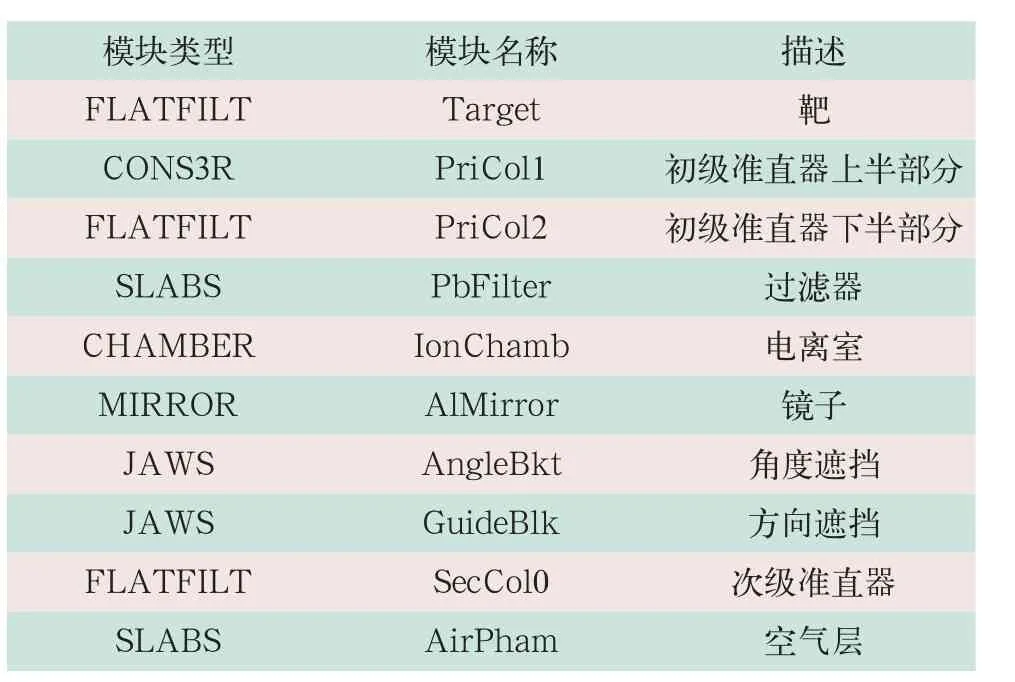
表1 Cyberknife模型中所使用的模块与顺序

2 结果

2.1 PDD

平均能量(Ē)的大小直接影响PDD，且与准直器大小关系不大[11]。为了确定平均能量(Ē)的大小，从5.9 MeV到7.5 MeV之间，每0.1 MeV取1个能量值，观察不同能量得到的PDD，与机器实测PDD进行对比，要求全局90%以上点的误差控制在2%之内，从而确定一个最符合目标的能量值(如图3所示)。

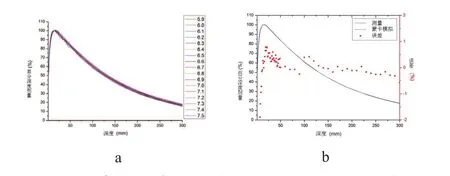
图3 准直器60 mm条件下束流PDD曲线图

由于建成区的影响，1 cm以内数据的误差较大，但是随着深度的加大，测量结果越来越稳定，且波动也小，最终确定Ē的值为6.9 MeV[12](见表2)。

2.2 OAR

束流强度分布FWHM[13]直接影响OAR，所以通过调节束流强度分布FWHM值，将会得到各准直器的OARs，分别与测量的5个不同深度(15 mm、50 mm、100 mm、200 mm及300 mm)的OAR曲线进行对比，要求全局90%以上点的误差控制在2%以内(半影区的误差较大，有些点甚至达5%)，从而可得到一个准确的束流强度分布FWHM值(如图4所示)。

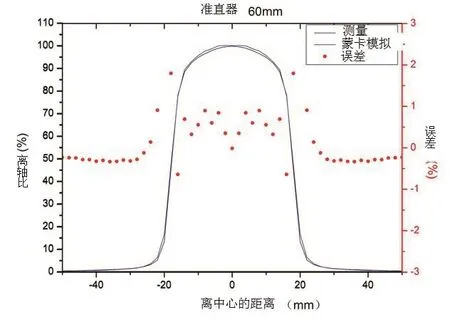
图4 蒙特卡罗模拟与测量OAR曲线及其偏差情况示图

由于水的波动等干扰对测量结果的影响，模拟结果与实测结果存在一定偏差。虽然FWHM等于0.4与0.5时，误差＜2%的点均为93.44%，但是当FWHM等于0.4 cm时的点误差最大为3%，而FWHM等于0.5 cm时的点误差最大为4%。因此，最终确定的束流强度分布FWHM值为0.4 cm，见表3。

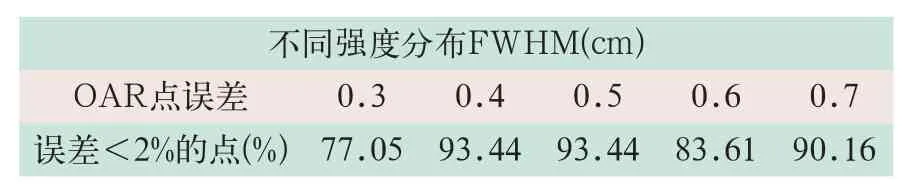
表3 不同强度分布FWHM情况下OAR点误差

2.3 射野输出因子

根据12个准直器的模拟数据(条件为SAD=800 mm，水下深度d=15 mm)，以60 mm准直器为基准，分别得出其他准直器的输出因子[14](见表4)与测量数据的比较(如图5所示)。

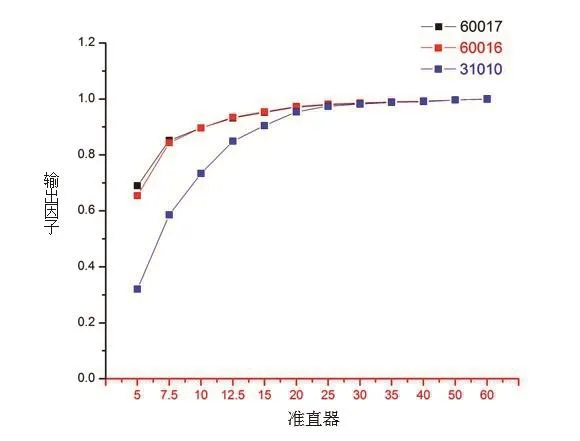
图5 各准直器输出因子散点图

由于电离室的灵敏度等原因，小野(＜15 mm)测量本身就存在较大误差可能，因此模拟结果与实测结果存在一定偏差。TPS射线追踪算法与TPS蒙特卡罗算法的输出因子较为接近，而BEAM蒙特卡罗得到的输出因子在小野(准直器15 mm以下)的情况下，略低于TPS自带的两种算法，而在大野(20 mm以上)的情况下则较为接近。

2.4 射线质

在SAD=100 cm、60 mm准直器的条件下，分别取水下深度为d1=10 cm和d2=20 cm的读数TPR10与TPR20，TPR20/TPR10得到射线质(Q)值为0.639，而实际测量Q值为0.635，误差＜1%。

2.5 修正因子(kQ,Q0)

通过蒙特卡罗方法模拟了CyberKnife系统，和标准条件下的60Co模型[15]以及Elekta Precise 6 MV加速器。Muir等[16]的研究结果显示，60Co模型(点源)在标准参考条件下的射线质Q0=0.664，通过模拟得到CyberKnife系统在标准参考条件下的射线质Q值，从而得到修正系数kQ,Q0。

然而不同的探测器由于其性能的差异，所得到的修正系数也不同，因此，针对以下3种探测器(见表5)，分别得到其修正系数(测量值与参考值之间的修正系数)和(测量值与标准值60Co)之间的修正系数，见表6。

表2 不同能量情况下PDD点误差

表4 各准直器在不同算法下的输出因子

表5 PTW电离室参数

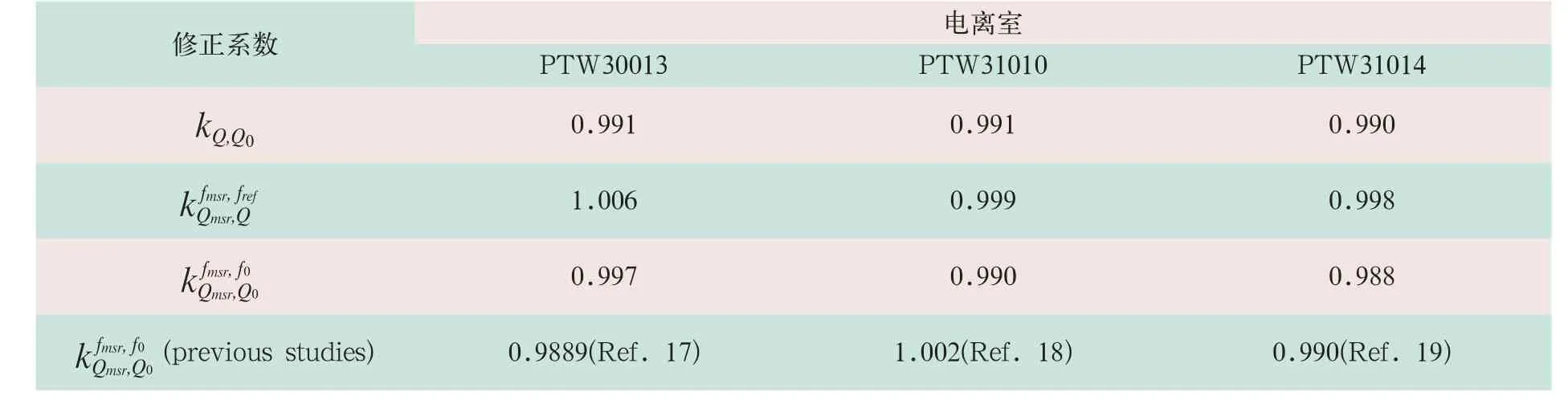
表6 各电离室修正系数

从表中可以看出，kQ,Q0在3种电离室之间的差别不大；在PTW31010和PTW31014电离室条件下接近于1，而在PTW30013条件下相差较大，这是由于PTW30013本身巨大的空腔体积导致了有效体积平均值的偏差；而与其他研究结果近似，在允许的误差范围内。

3 讨论

近年来，随着蒙特卡罗模拟应用的广泛，越来越多的人将其用来进行CyberKnife的研究。Araki[20]等利用蒙特卡罗软件模拟CyberKnife系统，将模拟所得的与实测的输出因子进行对比；Furweger[21]利用CyberKnife系统治疗的文件，读取出计划信息，从而进行了蒙特卡罗模拟的验证工作。Xiaoqing[22]等应用PENELOPE软件模拟了CyberKnife系统一部分准直器(10～60 mm)的PDD曲线，以及射线质等参数，得到射线质TPR20

10=0.632，与其测量所得0.640非常接近。本研究所建立蒙特卡罗束流模型，与实际测量数据对比(PDD、OAR)，全局范围内90%以上点的误差控制在2%之内，而修正因子和TPR20/10与实际测量数据相一致，且得到的修正因子也与其他相关研究相近，表明所建立的BEAM蒙特卡罗模型真实准确地模拟了CyberKnife系统束流场分布，即可应用此模型来进行一些剂量校准与验证，而不必通过繁琐的测量与运算，可以有效地避免一些不便于直接测量，或人为误差较大的测量。如CyberKnife在非标准参考条件下的剂量校准，尤其是小野的剂量校准。

本研究通过第三方软件平台，得到了一个可靠的束流模型，从而为后续研究奠定了基础。

[1]Eckhardt R.Stan ulam，john von Neumann，and the monte carlo method[J].Los Alamos Science Special Issue，1987(15 Special)：131-137.

[2]Walters BR，Kawrakow I，Rogers DW.History by history statistical estimators in the BEAM code system[J].Med Phys，2002，29(12)：2745-2752.

[3]Coste-Manière E，Olender D，Kelby W，et al.Robotic whole body stereotactic radiosurgery：clinical advantage of CyberKnife integrated system[J].Int J Med Robot，2005，1(2)：28-39.

[4]Adler JR，Murphy MJ，Chang SD，et al.Imageguided robotic radiosurgery[J].Neurosurgery，1999，44：1299-1307.

[5]朴俊杰，徐寿平，巩汉顺，等.CyberKnife系统技术评估和临床应用评价[J].医疗卫生装备，2016，37(3)：114-117.

[6]朴俊杰，徐寿平，王金媛，等.CyberKnife利用等中心及非等中心立体定向治疗计划质量及效率评价[J].实用癌症杂志，2016，31(5)：747-751.

[7]朴俊杰，徐寿平，段学章，等.CyberKnife中Fixed/Iris准直器对肝癌患者治疗计划的影响及评价[J].中国医学物理学杂志，2017，34(8)：762-765.

[8]Rogers DW，Faddegon BA，Ding GX，et al.BEAM：a Monte Carlo code to simulate radiotherapy treatment units[J].Med Phys，1995，22(5)：503-524.

[9]Walters BR，Kawrakow I，Rogers DW，et al.History by history statistical estimators in the BEAM code system[J].Med Phys，2002，29(12)：2745-2752.

[10]Kawrakow I，Walters BR.Efficient photon beam dose calculations using DOSXYZnrc with BEAMnrc[J].Med Phys，2006，33(8)：3046-3056.

[11]Tzedakis A，Damilakis JE，Mazonakis M，et al.Influence of initial electron beam parameters on Monte Carlo calculated absorbed dose distributions for radiotherapy photon beams[J].Med Phys，2004，31(4)：907-913.

[12]Abdel-Rahman W，Seuntjens JP，Verhaegen F，et al.Validation of Monte Carlo calculated surface doses for megavoltage photon beams[J].Med Phys，2005，32(1)：286-298.

[13]Sheikh-Bagheri D，Rogers DW.Sensitivity of megavoltage photon beam Monte Carlo simulations to electron beam and other parameters[J].Med Phys，2002，29(3)：379-390.

[14]朴俊杰，徐寿平，段学章，等.射波刀系统射野输出因子测量及对比[J].中国医学装备，2017，14(8)：17-20.

[15]Mora GM，Maio A，Rogers DW.Monte Carlo simulation of a typical60Co therapy source[J].Med Phys，1999，26(11)：2494-2502.

[16]Muir BR，Rogers DW.Monte Carlo calculations of kQ，the beam quality conversion factor[J].Med Phys，2010，37(11)：5939-5950.

[17]Araki F.Monte Carlo study of a Cyberknife stereotactic radiosurgery system[J].Med Phys，2006，33(8)：2955-2963.

[18]Pantelis E，Moutsatsos A，Zourari K，et al.On the implementation of a recently proposed dosimetric formalism to a robotic radiosurgery system[J].Med Phys，2010，37(5)：2369-2379.

[19]Kawachi T，Saitoh H，Inoue M，et al.Reference dosimetry condition and beam quality correction factor for CyberKnife beam[J].Med Phys，2008，35(1)：4591-4598.

[20]Araki F.Monte Carlo study of a Cyberknife stereotactic radiosurgery system[J].Med Phys，2006，33(8)：2955-2963.

[21]Fürweger C，Drexler C，Kufeld M，et al.Patient motion and targeting accuracy in robotic spinal radiosurgery：260 single-fraction fiducial-free cases[J].Int J Radiat Oncol Biol Phys，2010，78(3)：937-945.

[22]Xiaoqing D，Wenyun LUO，Kun YUE，et al.Monte carlo study on 6 MV photon beams of a CyberKnife stereotactic radiosurgery system[J].Nuclear Science and Techniques，2010，21(1)：16-19.