爱恩斯坦棋评估策略的研究

范博奇， 丁 濛,2， 张芳梓

(1 北京信息科技大学 计算机学院， 北京 100101; 2 北京信息科技大学 感知与计算智能联合实验室， 北京 100101)

引言

爱因斯坦棋[1]是2004年由德国中部耶拿镇数学教授Ingo Althöfer独创推出的两人骰棋类游戏。该棋种作为一种完全信息博弈项目，具有较高的随机性，看似是一个凭借运气的小游戏，背后却隐藏着较深的计算决策过程。

目前，国内爱恩斯坦棋规则与国际奥林匹克计算机博弈大赛的爱恩斯坦棋规则保持一致，棋盘为5×5的方格形棋盘，方格为棋位，左上角为红方出发区；右下角为蓝方出发区，棋盘设计如图1所示。

在计算机博弈软件的设计中，一个优良的评估策略往往是博弈取胜的关键，因其可为搜索过程的具体实现提供计算的基础。文献[2]设计了一种静态的攻防策略；文献[3]提出了偏向进攻的评估函数来削弱随机性带来的影响；文献[4]考虑到了棋子全歼的情况，建立了攻守兼备的估值函数进行决策。本文在文献[3]考虑进攻的基础上，对防守的情况展开综合分析，设计提出了一种新的评估策略。

1 评估策略的设计

爱恩斯坦棋的胜利方式分为率先占据敌方角落位和全歼对手棋子两种。经过大量的测试表明，以全歼对手棋子达到胜利条件的概率很低，所以研究中尽可能地将决策的目光投向角落位置上，尽快占据敌方角落点并防止敌方占据己方角落点，主要考虑了棋盘位置的价值和敌方棋子的位置。

本文针对爱恩斯坦棋的规则设计了评估函数，包括进攻与防守两个因素。其中，进攻是指寻求最短路径尽快到达敌方角落点，防守则是指在己方处于劣势的情况下，以保守的方式行棋，避免己方角落点被敌方到达或者己方被全歼。计算公式如下所示：

Value=k1×Attack+k2×Defense

(1)

其中，Value表示行棋走法中选择的评价估值；Attack表示进攻值；Defense表示防守值；k1、k2表示相应的参数。

由于爱恩斯坦棋策略中以全歼敌方棋子达到胜利的实现性远小于占据地方角落点的可能性，所以本文将着重讨论占据与防止被占据角落点的情况。

1.1 棋子进攻值的设定

爱恩斯坦棋行棋的棋子由每次掷出的骰子数决定，棋子的价值主要由棋子被选中的概率和棋盘相应位置的价值而确定。以己方作为左上方红方为例，率先占据右下角落位置为获胜。进攻策略的评估函数主要是根据棋盘不同位置设定的权重以及对敌方棋子的判断综合形成。

本文的设计原理是棋子的进攻值由棋盘相应位置的价值和敌方棋子的位置而确定，而边界值的棋子价值又应该略大于距离相同非边界值棋子价值。具体计算如公式(2)所示：

Attack[i][j]=boardvalue[i][j]-P[a]*distance

(2)

其中，i,j表示己方被骰子摇中的棋子可行棋的3个位置的坐标；Attack[i][j]为攻击值；boardvalue[i][j]表示棋盘不同位置的权重；a为敌方棋子编号；P[a]为该走法位置上的敌方棋子下一步行棋的概率；distance为该位置距己方角落点的最短距离。当该行棋位置无敌方棋子时，P[a]为0。

综上，给出了不同位置排定分布的棋子价值boardvalue[i][j]，如图2所示。

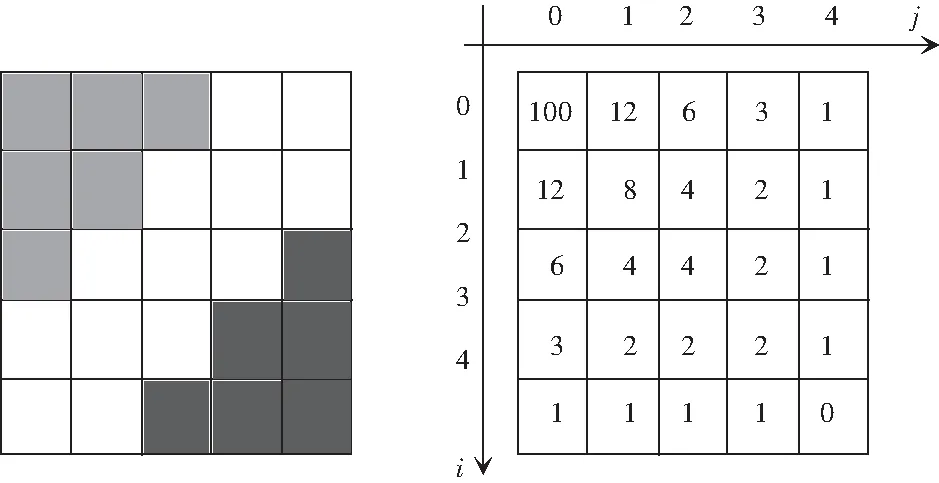
图1爱恩斯坦棋棋盘图2棋子分布价值

Fig.1ChessboardofEinsteinchessFig.2Thevaluedistributionofchess

图2表示当己方身处右下方时，在不同位置所分布的权重。若设从某一位置到敌方角落点的最短步数为n，则以24-n次幂作为权重分布在棋盘上，权重最高的是到达对方角落点路径最短的。对于己方来说，目标是到达左上角的点，因此越靠近该点，权重就越大。本文采选的是已占据角落点为目标的评估策略，所以在靠近敌方腹地时考虑到了因吃掉敌方棋子导致敌方骰子带来的随机性变小，从而对己方不利这一因素，添加了下一回合敌方棋子行动的概率值和该位置距己方角落点的最短距离两个变量，以便于综合衡定局面形势。而角落点位置为胜利的绝对先决条件，为此将该点的棋子权重改换为一个超过Value最大值的权重。此外，本文认定处在边界位置的棋子价值更高，原因解析如图3所示。

由图3可知，蓝1和蓝3距离对面角落点位置距离都是2，但是对于蓝3来说，因其同时面对红5和红3两个棋子的威胁，而蓝1只面对红5的威胁。因此可知，对于处在边界位置的棋子，将只会受到来自上方或者下方的棋子威胁(取决于初始位置)，而处在其他非边界位置的棋子，则会受到来自3个方向的棋子威胁，更不容易突破包围圈到达敌方角落点位置。所以在设置棋子价值的时候，边界位置的权值会偏高一些。

1.2 棋子防守值的设定

过程中，在斟酌防守层面设定时，一方面要建立动态的评估函数，另一方面要对特殊情况进行静态评估，保障该博弈系统的稳定性。

同时，不能仅仅关注本方棋子占据对面角落位置这一点，当对面棋子前进到己方腹地，对己方的角落位置产生足够威胁时，就要研究设计对敌方棋子的威胁排除了。

1.2.1 动态防守策略

本文的应对策略是，当有敌方棋子距离己方角落位置还有2步或者1步时，且己方棋子下一步行棋走法中有可吃掉敌方该棋子的局面，则此步走法计算防守值，否则防守值为0。防守值需基于敌方视角的棋盘价值而灵活设定。对其数学描述，可如式(3)所示：

Defense[i][j]=boardvalue[4-i][4-j]

(3)

若己方棋盘为右下角一方的话，此时己方相应的棋盘估值就要遵照敌方视角的敌方估值进行计算，根据己方棋子邻近位置的敌方棋子的价值来运作行棋，在受到不同位置棋子威胁的时候，选择其中最大的威胁位置予以行棋展开防守。

1.2.2 静态防守策略

当己方棋子个数小于等于2，且有被敌方全歼的可能时，将优先采取静态防守策略，目的是减小己方棋子被敌方棋子吃掉的概率，直观布局则可如图4所示。

在图4中，蓝2离敌方角落位置距离值为2，此时如果向斜上方走，极易落入敌方红2与红5的包围圈，己方棋子就会面临被全歼的可能。此时应该根据敌方下一回合中红5或红2行动的概率，选择向左或者向上的行棋方式，避开“包围圈”。但无论在何种棋局下，当己方有任意一枚棋子距离敌方角落位置仅为一步的时候，均将选择达到占据角落位置的胜利条件的走法。

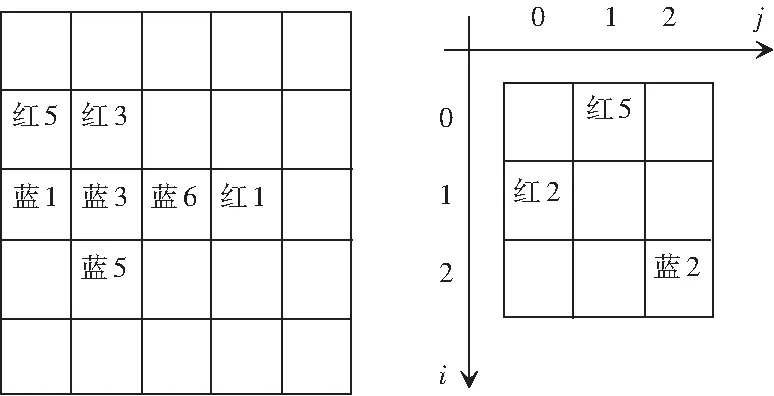
图3 对战局势 图4 静态防守棋局Fig. 3 The situation of confrontation Fig. 4 The chess game of static defense

2 评估策略实现流程

整个评估策略先从外部接收骰子数，根据棋盘上己方棋子情况选出可移动棋子和预期可行方案，再判断是否满足静态防守策略条件，若满足即根据相关局势算出下回合掷到敌方棋子概率，并开启走法选择流程；若不满足，则根据公式(1)计算评价估值，在比较所有走法的估值后选择最大权值的走法，从而转入输出环节操作。分析后，可得设计步骤如图5所示。

图5 评估策略流程图Fig. 5 The flow chart of evaluation strategy

3 实验结果与分析

本次爱恩斯坦棋项目结合了上文研究提出的进攻+防守并结合静态策略的评估策略，公式(1)中的k1、k2分别设为0.65和0.35,使用了Java语言编写研发，在Windows环境下分别设计展开了50次实验模拟，同时与表1中选用评估函数的程序进行对照比较，运行结果见表1。

表1 该博弈程序与其他程序的机机对战对比表Tab. 1 Comparison of this program with other programs

由表1可知，在使用了新评估策略后，面对只使用进攻策略评估函数的程序具备了很高的保障，在面对无静态防守策略评估函数的程序也占有一定的胜率。该实验结果清晰证明了这种评估策略对胜利条件的实现有着积极有效的正向作用。

4 结束语

本文设计提出了一种新的爱恩斯坦棋评估策略，对棋子各位置价值融入了研究改进，在实现了进攻与防守评估函数的同时，添加了静态层次的防守策略设计，达到了较好的效果。

[1] 中国人工智能学会机器博弈专业委员会. 爱恩斯坦棋项目规则[EB/OL]. [2016-08-14] .http://computergames.caai.cn/jsgz09.html.

[2] 周文敏,李淑琴. 爱恩斯坦棋静态攻防策略的研究[J]. 电脑知识与技术,2014,10(5):1027-1031.

[3] 黄恩一,丁濛. 基于爱恩斯坦棋削减随机性影响的博弈算法研究[J]. 智能计算机与应用,2017,7(1):69-70，75.

[4] 光洋. 爱恩斯坦棋计算机博弈系统的研究与实现[D]. 合肥：安徽大学,2016.