货币政策与股市行情的关联性研究

◇占斯亚

近年来，沪深股市多次剧烈震荡，引发投资者恐慌。面对股票价格的异常波动，有关部门曾多次运用货币政策维护股票市场基本稳定，因此货币供应量对股票价格的影响在实践上是存在的，但就理论而言，影响股价的因素非常复杂，多数研究者认为传统的货币供应量与利率渠道是最为重要的影响因素，其他因素可能正是因为强化了利率效应从而影响了股价。本文将借鉴国外学者Breitung和Candelon（2006）提出的频域格兰杰因果检验方法，基于MATLAB软件，从频率领域研究不同层次货币供应量、利率对股票价格的影响，挖掘被传统时域研究方法忽略的深层次关系。

一、研究方法与数据选取

1.研究方法

首先，假设有一组三维时间序列向量 xt=[x1t，x2t，x3t]'，t=1，…，T，然后建立一个阶的向量自回归VAR(k)模型：

其中μ为3维的常数向量，εt为白噪声过程，即满足Ε（εt）=0，Ε（εtεt'）=Ω，Ω 为对称正定矩阵，Θ1，Θ2，…，Θk为 3×3 阶系数矩阵。

其次，再定义系数矩阵Θt（t=1，…，k）里的第（1,3）个变量为 θ13,t，然后由此得到一个系数向量 β=[θ13,1，θ13,2，…，θ13,k]'，并给定R矩阵如下：

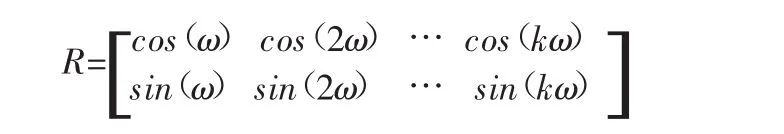
其中 ω∈（0，π）。最后，根据 Breitung和 Candelon（2006）提出的方法，如果时间序列是平稳的，那么x3t在频率ω处不能格兰杰引起x1t变化的零假设可表示为：

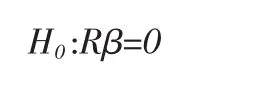
并可以证明与上述零假设相对应的统计量，近似服从自由度为2的x2分布。

以上正是本文研究使用的频域格兰杰因果检验方法，笔者还将配合MATLAB软件将研究结果图示化。

2.数据选取

本文数据来源于中经网统计数据库，选取的研究对象有货币供应量、利率及股票价格，样本选取了1997年1月～2016年12月的月度数据。变量分别选取了狭义货币供应量M1、广义货币供应量M2、当月银行间同业拆借加权平均利率R及我国最具代表性的上证指数SHS和深证指数SZS。

除利率R外，以上所有数据均取自然对数，本文采用ADF和PP检验对数据进行了平稳性检验，结果如下所示。

表1 平稳性检验

从表1中我们发现，在5%的显著性水平下除利率R外，原始数据均不平稳，在一阶差分化后，仍在5%显著性水平下，ΔlnSHS、ΔlnSZS、ΔR在ADF检验与PP检验中均表现平稳；而ΔlnM1和ΔlnM2虽在ADF检验中不平稳，但在PP检验中检验值分别为-18.42303、-17.14753，显著拒绝原假设，因此也是平稳的，因此本文认为 ΔlnM1、ΔlnM2、ΔlnSHS、ΔlnSZS 及 ΔR是一阶单整的平稳时间序列数据。

二、实证结果分析

1.模型构建

根据频域格兰杰因果检验方法，并运用经一阶单整的时间序列数据，本文将构建4个向量自回归VAR（k）模型，分别如下所示：

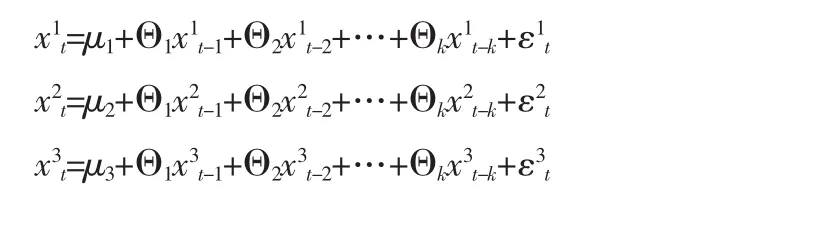
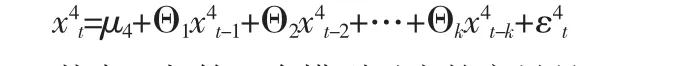
其中，与第一个模型对应的变量是x1t=[ΔlnM1,ΔR,ΔlnSHS]'，与第二个模型对应的变量是 x2t=[ΔlnM1,ΔR,ΔlnSZS]'，与第三个模型对应的变量是 x3t=[ΔlnM2,ΔR,ΔlnSHS]'，与第四个模型对应的变量是 x4t=[ΔlnM2,ΔR,ΔlnSZS]'。

2.模型最优滞后阶数的确定

根据所构建的VAR模型，本文使用Eviews软件，通过LR、FPE、AIC、SC、HQ五个准则来选取最优滞后阶数,并以通过准则最多的阶数为最优阶数。最终得出模型一的最优滞后阶数为5阶；模型二的最优滞后阶数为4阶，模型三的最优滞后阶数为5阶；模型四的最优滞后阶数为4阶。

3.频域因果关系

如图 1所示，横轴表示频率 ω,ω∈（0，π），且频率 ω可以通过公式T=2π/ω换算时间周期；纵轴表示Wald统计量；黑色实线表示频域格兰杰检验值，黑色虚线表示在5%显著性水平下的临界值（5.99）。

（1）整体样本区间结果

首先，在整体样本区间对模型一、二进行频域格兰杰因果检验，得到了狭义货币供应量M1、利率R与股票价格的频域因果关系。如图1所示，可以发现：当频率ω∈（2.3437，π）时，M1对深证指数SZS影响显著，说明M1是引起深证指数SZS变动的格兰杰原因，时间周期为1.97～2.68个月；但R在整个频率区间对上证指数SHS、深证指数SZS影响均不显著。

图1 整体样本区间M1、R与股票价格的频域格兰杰因果检验

然后又在整体样本区间对模型三、四进行频域格兰杰因果检验，得到了广义货币供应量M2、利率R与股票价格的频域因果关系，并发现：在整个频率区间，M2、R对上证指数SHS、深证指数SZS影响均不显著，说明M2、R均不是引起股票价格变动的格兰杰原因。

综合上述结果，在整体样本区间中，只有M1对股票价格产生显著影响，且M1的变动能在短期1.97个月后影响股票价格，因M1代表的是流通中现金M0和活期存款的总和，通常能够反映居民和企业投资资金的松紧变化，是经济周期的先行指标，而M2、R对股票价格却均没有显著性影响，这与刘熀松（2004）等学者的研究结论一致。

（2）分段样本区间结果

为深入挖掘变量的深层次因果关系，本文运用Lutkepohl and Kratzig(2004)介绍的chow模型稳定性检验方法，对整体样本区间的VAR模型进行了chow模型稳定性检验，结果如下：

表2 规模稳定性检验

从表2我们发现上述四个VAR模型均不平稳，在2003年12月份左右均存在着一个结构性断点；又因2003年末我国房地产、汽车及钢铁行业发展过热，为抑制投资过热和通胀趋势，政府实施收紧银根、上调存款准备金率等紧缩性货币政策，股票市场由过热转向疲软。因此本文选择2003年12月为模型的统一分断点，将整体样本分割成1997年1月～2003年12月和2004年1月～2016年12月两个平稳的分段样本区间。

第一分段样本区间（1997年1月～2003年12月）

首先，在第一分段样本区间对模型一、二进行频域格兰杰因果检验，得到了狭义货币供应量M1、利率R与股票价格的频域因果关系，如图2所示，可以发现：当频率时，M1仍然对深证指数SZS影响显著；当频率时，R对深证指数SZS首次出现短暂的显著性影响，表明R是引起深证指数SZS变动的格兰杰原因，且时间周期为1.97～2.96个月。

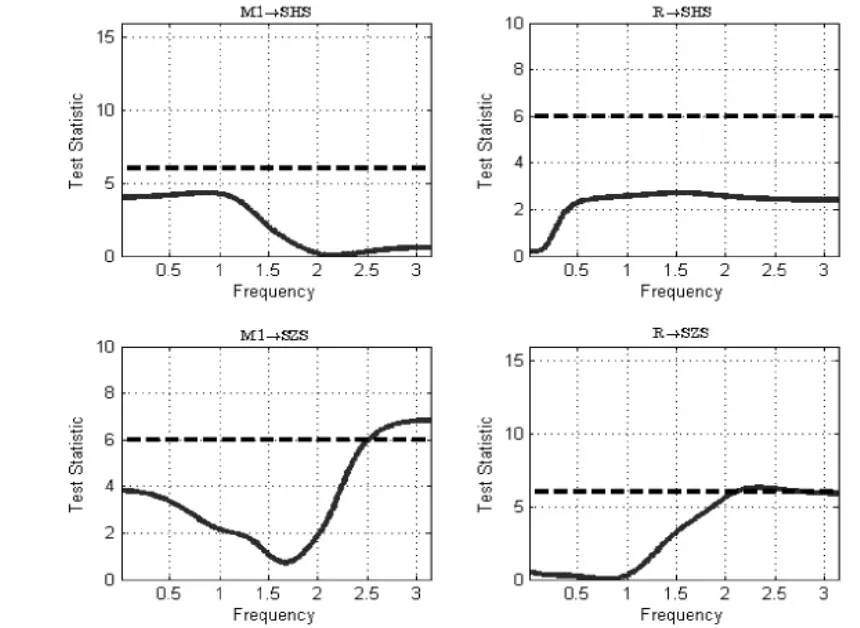
图2 第一分段样本区间M1、R与股票价格的频域格兰杰因果检验

其次，又在第一分段样本区间对模型三、四进行频域格兰杰因果检验，得到了广义货币供应量M2、利率R与股票价格的频域因果关系，如图3所示，可以发现：当频率ω∈（0，1.75）时，M2对上证指数SHS首次出现显著性影响，表明M2是引起上证指数SHS变动的格兰杰原因,且时间周期为3.59～+∞月；当频率ω∈（2.15，2.25），R对深证指数SZS也短暂出现显著性影响。

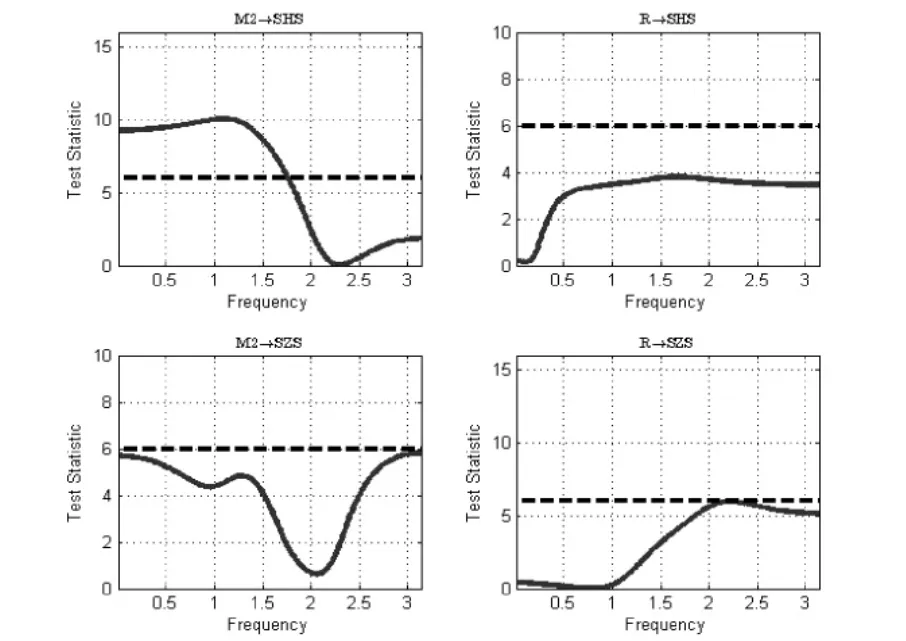
图3 第一分段样本区间M2、R与股票价格的频域格兰杰因果检验

第二分段样本区间（2004年1月～2016年12月）

在第二分段样本区间，笔者同样对模型一、二、三、四进行了频域格兰杰因果检验，并发现：在整个频率区间，M1、M2、R对上证指数SHS和深证指数SZS均没有显著性影响，则在第二分段样本区间M1、M2、R均不是引起股票价格变动的格兰杰原因。

总结上述分段结果，可以发现：在第一个分段样本区间，M2和R对股票价格均首次出现了显著性影响，且M2对股票价格影响在3.59个月后才体现出来，因M2代表的是M1、定期存款及居民储蓄的总和，且由于股市波动，居民投资者青睐于收益稳定的储蓄存款和固定收益证券，因而M2中执行贮藏职能的货币比重较高，反应滞后期较长。

三、结论与建议

本文运用频域格兰杰因果检验，在考虑模型稳定性的基础上，实证研究了不同层次货币供应量及利率对股票价格的影响，具体结论与建议如下：

1.在整体样本区间，M1对股票价格有显著性影响；在第一个分段样本区间，M1对股票价格仍有显著性影响，但在第二个分段样本区间，M1的显著性消失了。这说明在整体样本区间M1的显著性，很可能是由于第一个分段样本区间M1的显著性而导致的，因此学界应结合实际情况，审慎看待研究结果，不能高估M1对股票价格的影响。

2.在整体样本区间，M2对股票价格没有显著性影响，但在第一个分段样本区间，M2对股票价格却首次出现显著性影响，且影响在中长期后（3.59个月）才体现出，但M1的变动一般在短期后（1.97个月）影响股票价格，这与不同层次货币供应量的统计口径相关，因此政府要权衡不同层次货币供应量的预测能力，考虑货币政策执行的滞后期，相机抉择的货币政策。

3.在整体样本区间，利率R对股票价格没有显著性影响，但在第一个分段样本区间，R对股票价格首次出现短暂的显著性影响，这反映在特定的时期，利率波动对股价是存在影响且非常迅速的（高频），因此政府和投资者应该结合实际情况重视利率对股票价格及宏观经济的间接影响，推动利率市场化进程，完善货币传导机制。