铁路网络列车运行调整的优化模型及其分支定价算法

兰泽康，何世伟，黎浩东

(北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京100044)

0 引言

当列车出发晚点、运行晚点、临时加开列车或列车早点到达等情况发生时，都会导致列车运行偏离图定时刻，为了恢复列车安全有序运行，需要采取列车运行调整措施.目前列车运行调整研究主要集中于单条线路，限制了调整的空间，若可以扩展至一定区域的线路网络，则可以充分利用其他线路上空闲的资源，达到整体的优化效果.但铁路网络求解规模较大，不易快速求解，而列车运行调整实时性要求较高，故需要设计高效的算法.

在铁路网络列车运行图方面，彭其渊等[1]在列车选择线路固定条件下，提出采用加边法求解；Meng等[2]建立铁路网络列车运行调整的MILP模型，利用拉格朗日松弛算法化解成单列车的最短路径问题；陈雍君等[3]考虑微观路网的复杂性采用了序优化算法；Mu等[4]提出了多种启发式方法，包括初始化候选路径集，以及从路网或列车数量角度分解成小规模问题滚动求解的方法.可以看出研究方法大多采取不同的分解策略，达到简化求解的目的.本文首先在文献[2]研究成果的基础上，建立基于列车到发时刻的MILP模型，再构建基于列车时空路径的ILP模型，设计分支定价方法求解.

1 问题描述与模型假设

1.1 问题描述

相对于单条线路，铁路网络的列车运行调整问题，每一列列车可能有多条行驶线路可以选择.如图1所示，是由2条单线铁路和3个车站组成的调度区段，标有数字的节点指轨道电路的分界点，连接相邻两个节点的弧段指区间内闭塞分区或车站内股道线路.图中矩形方框表示相应弧段在某一时间段内进行维修作业，期间不可被列车占用.正常情况下，列车可按照既定的计划有序地在该网络上运行.当列车晚点进入调度区段时，就可能与其他列车和维修作业发生冲突.假设可以变更列车运行线路的条件下，需要重新调整列车运行计划，使得列车尽可能按图定时刻到达终点.

现有研究大多将车站看作是一个点，到发线数量约束作为模型的约束条件，如文献[5].本文考虑车站内进路，将到发线运用和列车时刻表一同优化，因此可以不必单独考虑车站能力约束，但同时也造成求解规模增大.

1.2 模型假设

假设1将列车看作是一个质点，列车可选择任意1条从始发节点到终到节点的可达路径，包括更改运行线路和变更站内到发线.

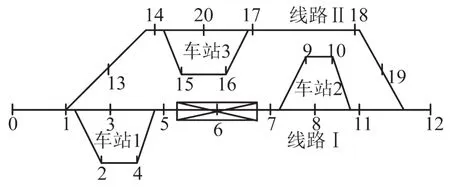
图1 铁路网络示意图Fig.1 Sketch map of railway network

假设2不考虑停站变动的影响.正线不允许停车，只准在侧线上停车，例如图1中的2-4、15-16和9-10弧段为侧线.

假设3已知维修作业的开始时间、结束时间及作业地点.每一个维修作业所占用的弧段是紧邻的.

2 基于列车到发时刻的模型建立

2.1 基本符号定义

给定铁路网络G=(V,A)，其中V为节点集合，A为弧段集合，v∈V，a∈A；G内所有运行的列车集合为F，f∈F，列车f有唯一索引If=0,1,…,|F|-1；列车f的始发节点为of，终到节点为df；Af为列车f可能通过的弧段集合，As为允许停车的弧段集合；A o(v)和A d(v)分别为以v起点和终点的弧段集合；Rf(a)为列车f在弧段a上的最小运行时间分别为列车f在弧段a(a∈As)上的最小和最大停留时间；h为列车车头安全间隔时间，即统一所有安全间隔时间为h；Sf为列车f最早可能始发时间；Ef为列车f图定终到时间；K为维修作业集合，k∈K；M为足够大的正整数.

决策变量sf(a)和ef(a)分别为列车f到达和离开弧段a的时间；yf(a)表示列车f是否通过弧段a的二元变量，是则取值为1，否为0；λ(f,f′,a)为二元变量，当列车f′在f之后通过弧段a时，取值为1，否为0.

2.2 约束条件和目标函数

(1)流平衡约束.

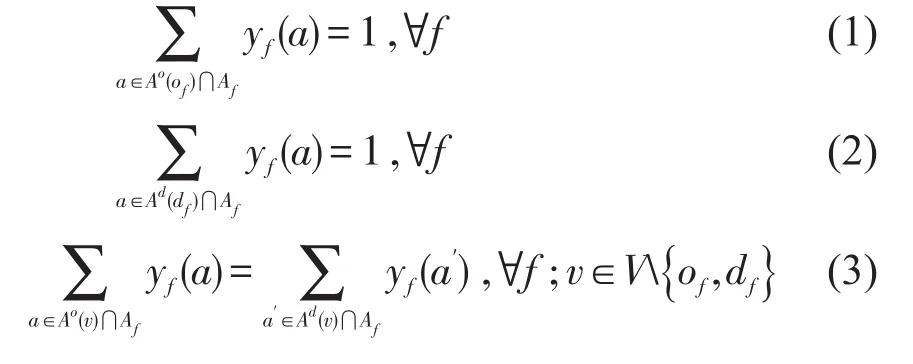
式(1)和式(2)分别保证列车在始发节点和终到节点的流平衡，式(3)保证列车在中间节点的流平衡.

(2)最早发车时间及时间变量相关约束.

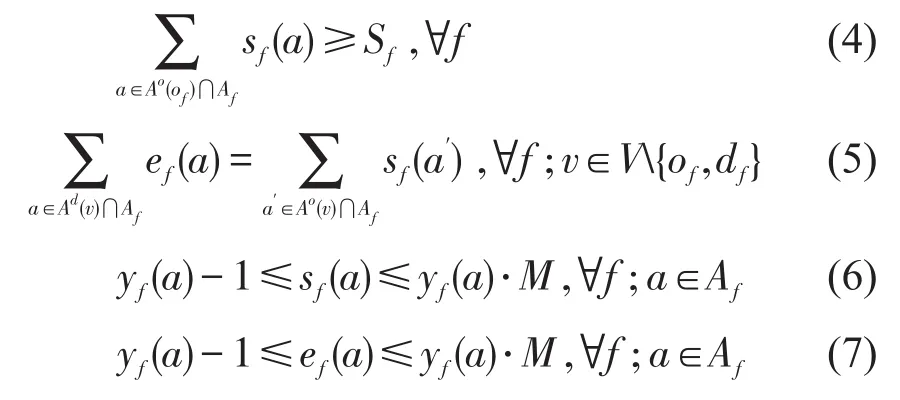
式(4)为列车最早允许出发时间约束；式(5)表示列车离开前一弧段与到达下一相邻弧段的时间相等；式(6)和式(7)表示当列车f不占用弧段a时，则sf(a)和ef(a)均取值为 0.

(3)最小运行时间和停站时间约束.

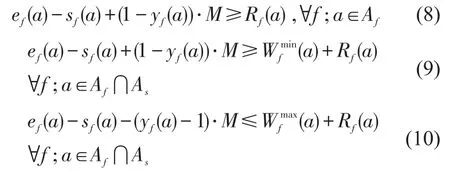
式(8)为最小运行时间约束；式(9)和式(10)分别将最小停站时间和最大停站时间附加到弧段运行时间上，以满足停站时间约束.

(4)安全间距约束.

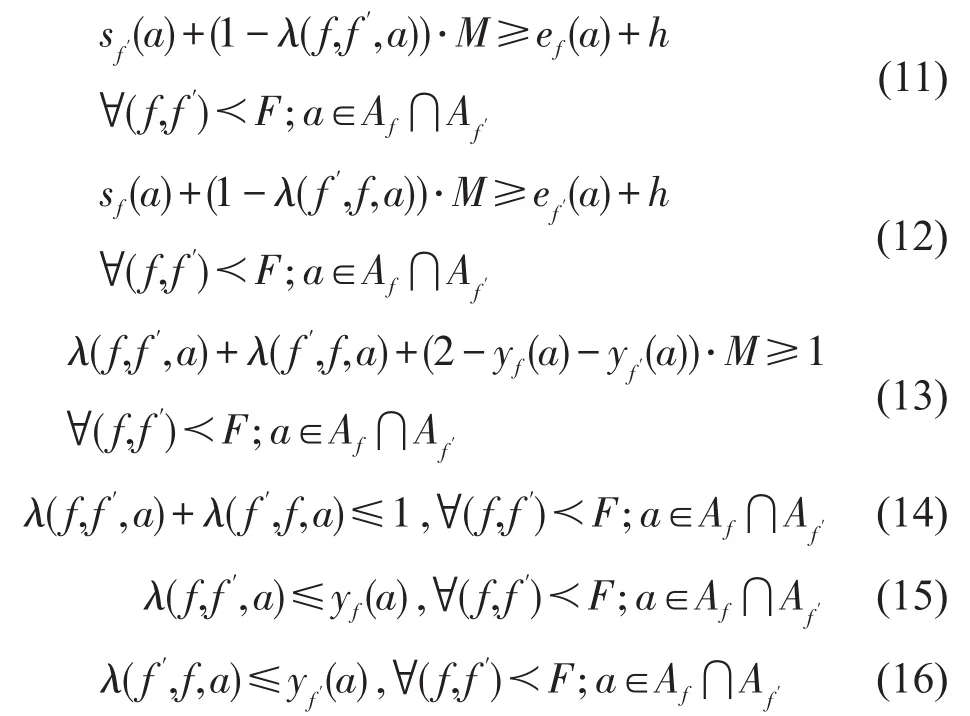
式(11)表示当列车f和f′都占用弧段a，且f′在f之后占用时，f′到达弧段a时间与f离开弧段a的时间应间隔h，(f,f′)≺F表示F中满足If′＞If的两列车；式(12)与式(11)同理；式(13)表示当列车f和f′都占用弧段a时，有λ(f,f′,a)+λ(f′,f,a)≥ 1，结合

式(14)，得到λ(f,f′,a)+λ(f′,f,a)=1，即f在f′之前或之后占用a；式(15)和(16)表示列车f或f′不占用a时，λ(f,f′,a)和λ(f′,f,a)均取值为 0.

(5)维修作业约束.

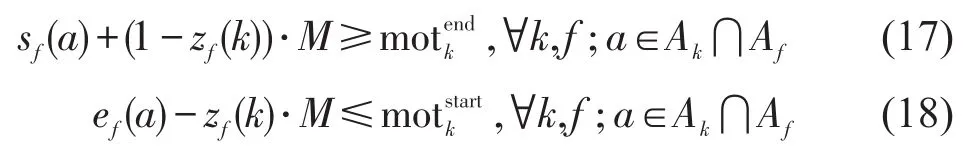
式中：Ak为维修作业k所占用弧段集合分别为维修作业k的开始时间和结束时间；zf(k)是二元变量，当列车f在维修作业k结束之后通过弧段a(a∈Ak)时，取值为1，f在维修作业k开始之前通过a或不通过a时均取值为0.

式(17)表示当列车f在维修作业k结束之后通过弧段a时，应满足sf(a)≥moteknd；式(18)表示当列车f在维修作业k还未开始时通过弧段a，或者不通过a，应满足ef(a)≤motstartk.

(6)目标函数及相关约束.

3 基于列车时空路径的模型建立

为刻画列车在铁路网络上运行的时空路径，如图2所示，以铁路网络为空间平面，并加上时间轴，形成三维的立体空间.以固定时间长度离散化时间轴，为平衡求解精度和时间，本文取固定时长为1 min.用时间拓展的时空联弧(v1,v2,t,s)连接节点v1和v2，t、s分别表示到达节点v1和v2的时间，顺次连接列车经过的所有节点，即形成1条时空路径p，p在空间平面上的投影即为列车在铁路网络中实际通过的物理路径.

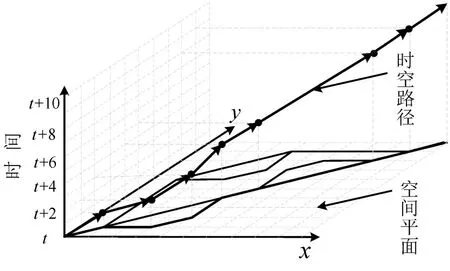
图2 列车在铁路网络中运行的时空路径Fig.2 The time-space path of train on a railway network

假设开始调整的时间为0，调整时段长为T.令Pf为列车f所有可能的时空路径集.cf(p)为p(p∈Pf)的费用，若p的终到时间为则cf(p)可按式(23)计算.

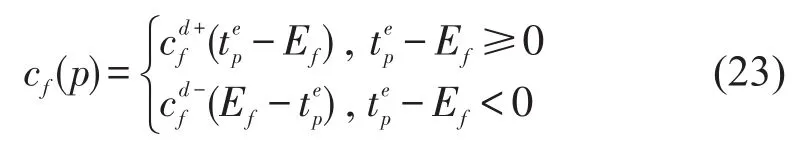
xf(p)为列车f是否选择p(p∈Pf)的二元变量，若选择则取1，否取0.为满足列车安全间距要求，需要保证任意弧段在时间段[τ,τ+h-1](τ=1,2,…,T-h)内至多被1列列车占用，定义Pf中在该时间段内占用弧段a的时空路径集为Pf(a,τ,τ+h-1).建立基于列车时空路径的模型M2为

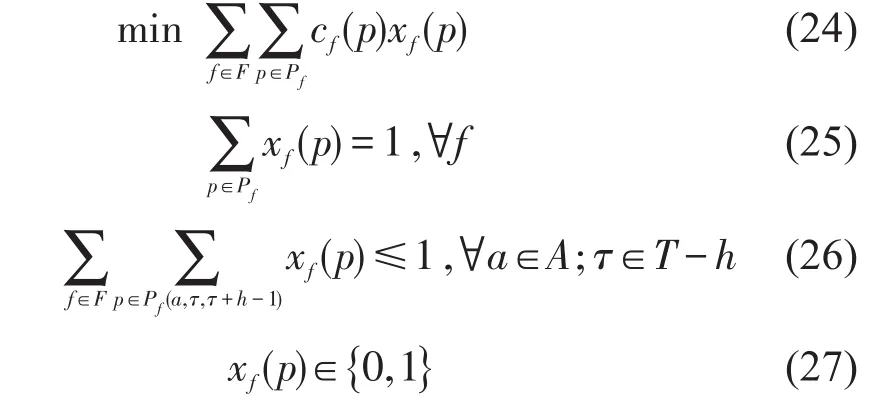
式(24)为目标函数，表示最小化所需费用；式(25)表示列车f选择Pf中唯一的1条时空路径；式(26)确保被选择的任意2条时空路径满足安全间距要求.

模型M2与文献[5]模型主要有以下几点不同：①本文定义了每1列列车的可选路径集，而文献[5]中只定义了1个可选路径集；②由于本文考虑了车站内轨道电路设置，不必单独考虑到发线数量约束，且不同于文献[5]以车站到发间距描述安全间隔，本文以任一弧段不被2列列车同时占用进行描述.

4 求解模型M2的分支定价算法

分支定价算法是一种将列生成算法和分支定界算法相结合的组合算法.由于列生成算法所得到的解一般不是整数解，需要借助分支定界算法对非整数变量分支以获取整数解，每个子结点仍采用列生成算法求解.以下是基于目标函数为最小化，0-1整数规划问题为前提进行分析的.

4.1 求解线性松弛模型的列生成算法

上述模型M2结构简单，但缺点在于列车可选时空路径数量是非常巨大的，无法一一枚举，因此采用列生成算法定价生成路径的方法.首先将M2分解成限制主问题RMP和|F|个子问题，列车f对应的子问题为SPf.令P′f表示Pf的子集，替换M2中的Pf，且将式(27)线性松弛，即构成RMP.在RMP求解之后，可以得到对偶最优解(μ,λ)，其中μ=(μf)，λ=(λ(τ,a))分别为式(25)和式(26)的对偶变量，则SPf求解模型为

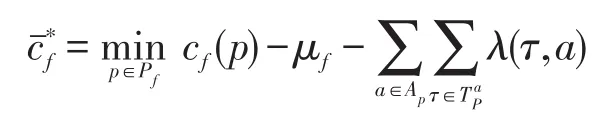
式中：AP为所包含的弧段集合为上弧段a所对应的时空联弧在时间轴上投影所包含的时间点集合.

将λ(τ,a)看作是在τ时刻占用弧段a的价格，结合时空路径的形成，子问题可转化成求每1列列车的最短路问题，本文最短路算法采用的是文献[2]中离散时空标号更新算法.若SPf的目标值，则在P′f中添加当前最短路，否则不需要添加.RMP和子问题不断迭代求解，直至所有子问题都没有添加新的路径时终止，可获得模型M2线性松弛后的最优解，它是模型M2的下界值.

4.2 获取整数解的分支定界算法

分支求解过程较为耗时，需采用加快算法收敛的分支策略和结点搜索策略.本文采用的分支策略为伪费用分支[6-7](Pseudocost Branching).其主要思想是给每个变量定义相应的评估值，每次选择出分支后最有可能使得下界值更快上升变量进行分支.对于一个非整数变量xi，若对其分支可得目标值对xi变化的敏感度为

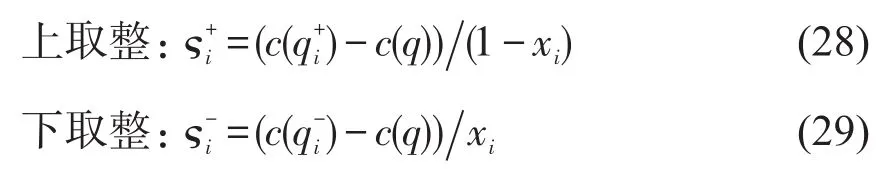
式中：c(q)为父结点的目标值分别为对变量xi上、下取整之后得到子结点的目标值.

由于xi可能多次被分支，记的累计值分别为累计次数分别为若子结点的RMP问题不可行则不予累计，最终xi的评估值按式(30)计算，每次选择评估值最大的变量进行分支.由于在分支树的开始阶段，大部分变量没有被分支过，无法计算评估值，可采用强分支(Strong Branching)方法对评估值进行初始化，这里不在赘述，可以参见文献[6-7].

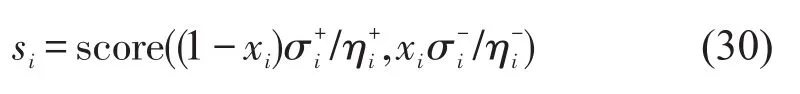
式 中 ：score(s+,s-)=(1-μ)∙min(s+,s-)+μ∙max(s+,s-)，μ=1 6.

分支中上取整对目标值的影响较大，也可能是无解的，而下取整对目标值的影响较小，故本文仅对上取整得到的子结点用列生成算法求解，而下取整的子结点添加取整约束后用对偶单纯形算法求解以获取目标值，进一步加快算法收敛.为便于后续论述，记上取整得到的子结点为右结点，而下取整得到的子结点为左结点.结点搜索采用最佳优先(Best-node First)搜索策略，即每次选择目标值最小的结点，使得下界可以更快地上升.

4.3 处理众多约束条件的行生成方法

4.4 算法流程

算法流程中涉及到的符号定义如表1所示.

Step 1获得初始可行解和初始化.

按照列车最早可能出发时间，依次对列车按照最短路算法进行规划，获得可行解的目标值作为UB的初始值，令LB=0.创建1个结点，以初始可行解建立该结点的RMP问题，将其加入ANL.

Step 2终止条件.

表1 算法流程中的符号定义Table 1 Notations for the algorithm flow

Step 3结点选择.

以最佳优先搜索策略从ANL中选择1个结点作为当前结点n，将n从ANL中移除.若n是左结点，用对偶单纯形算法求解RMP(n)，否则用列生成算法求解RMP(n).

Step 4结点操作判断.

若RMP(n)不可行或Z(n)≥UB，转Step2；若B(n)=1，更新UB，转Step 2；若B(n)=0，转Step5.

Step 5分支.

按照伪费用分支策略分支，生成右结点和左结点，并在RMP(n)的基础上添加分支变量的取整约束，构建相应子结点的RMP问题，将2个子结点加入ANL，转Step2.

5 算例分析

5.1 算例数据

本文算例设计铁路网络共有76个节点和85个弧段，总长度137.6 km，如图3所示.维修作业和部分列车相关数据分别如表2和表3所示，列车晚点进入区段的时间分布在[0,20]min范围内.计划运行图中所有列车均未通过交叉渡线(图3中54-58，56-57，44-47，45-46)，而列车运行调整后，列车可能通过交叉渡线从一条线路换轨至另一条线路.

表2 维修作业相关数据Table 2 The data for maintenances

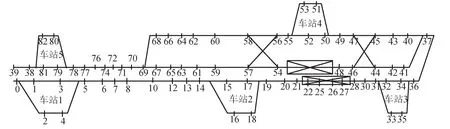
图3 算例的铁路网络Fig.3 The railway network for numerical experiment

表3 部分列车相关数据Table 3 The data for some trains

5.2 算法性能分析

为分析本文分支定价算法的性能，用2种方法分别求解算例，测试计算机参数为Intel Pentium CPUB9602.20GHZ，6GB内存.求解结果如表4所示.

(1)IP_GUROBI.运用求解器GUROBI6.5.0求解基于列车到发时刻的模型.

(2)BAP_C#.运用C#语言实现分支定价方法求解模型M2，以GUROBI作为LP求解器.

求解结果表明，随着列车数量的增多，即求解规模的增大，IP_GUROBI方法求解越来越困难，列车数为4列时，5.3 s即可得到最优解，当列车数增加到20列时，求解时间达到3 468 s.在规模较小时，IP_GUROBI比BAP_C#更具有优势，随着规模增大，BAP_C#可以在较短的时间内获得满意解，如列车数量为20列时，求解时间减少(3 463.7-290)/3 463.7=91.6%，得到的最终可行解距离最优解的间隔为(508-463)/463=9.72%.

在分支策略中，一种较为常用的分支策略是最为分数分支(Most Fractional Branching)策略，即每次选择最接近0.5的变量进行分支[6-7].现以列车数为20列的情况为例，比较本文分支策略和最为分数分支策略，两者的上下界收敛曲线如图4所示.本文分支策略在290 s处收敛，最终收敛目标值为508 min，而最为分数分支策略在389 s处收敛，最终收敛目标值为515 min，说明了本文分支策略具有一定优势.需要指出，最终收敛时上下界相等并不是得到了最优解，因为分支树中的某些结点没有用列生成算法求解.

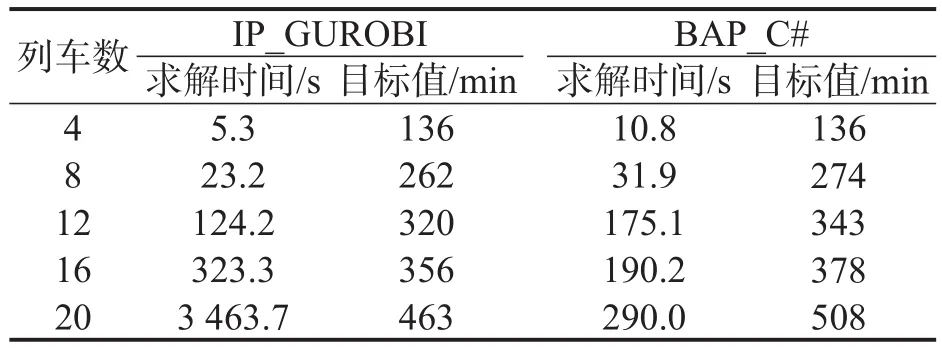
表4 IP_GUROBI和BAP_C#的求解时间和目标值Table 4 The computational time and objective value for IP_GUROBI and BAP_C#

5.3 可变更线路与按原始线路行驶的比较

本文按原始线路行驶指的是限定列车不能使用交叉渡线，同样用GUROBI求解得到该种调整方式的目标值，结果如图5所示.可以看出，可变线路相比于按原始行驶线路得到优化，目标值降低31.4%～41.9%，平均降低37.4%.

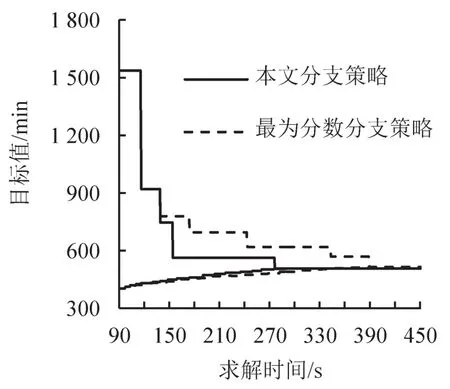
图4 不同分支策略上下界收敛曲线Fig.4 The upper and lower bound for different branch strategies

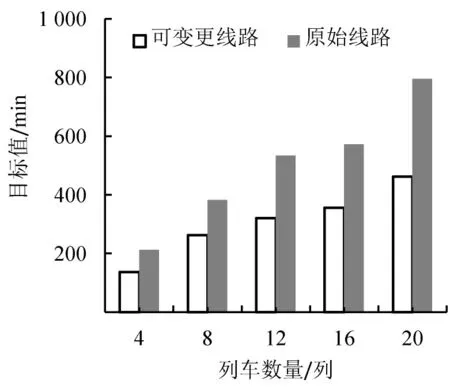
图5 2种列车运行调整方式的目标值Fig.5 The objective value for two kinds of train rescheduling

6 结论

本文分别构建了基于列车到发时刻和基于列车时空路径的铁路网络列车运行调整模型，前者适用于商业软件求解，可获取最优解.结合后者模型的特点，设计了分支定价算法求解，对比得出随着求解规模的增大，本文算法求解时间变化较为平缓，且能够得到较优解，表现出更好地适应性.同时得出本文分支策略比最为分数分支策略可以更快地使算法收敛，可变更线路相对于按照原始线路行驶的调整方式可降低目标值31.4%～41.9%.

[1]彭其渊，朱松年，王培.网络列车运行图的数学模型及算法研究[J].铁道学报，2001，23(1):1-8.[PENG Q Y，ZHU S N，WANG P.Study on a general optimization model and its solution for railway network train diagram[J].Journal of the China Railway Society，2001，23(1):1-8.]

[2]MENG L Y，ZHOU X S.Simultaneous train rerouting and rescheduling on an N-track network:a model reformulation with network-based cumulative flow variables[J].Transportation Research Part B Methodological，2014，67(3):208-234.

[3]陈雍君，周磊山.基于序优化方法的列车运行调整算法研究[J].铁道学报，2010，32(3):1-8.[CHEN Y J，ZHOU L S.Study on train operation adjustment algorithm based on ordinal optimization[J].Journal of the China Railway Society，2010，32(3):1-8.]

[4]MU S，DESSOUKY M.Scheduling freight trains traveling on complex networks[J].Transportation Research Part B Methodological，2011，45(7):1103-1123.

[5]CACCHIANI V，CAPRARA A，TOTH P.A column generation approach to train timetabling on a corridor[J].4or Quarterly Journal of the Belgian French&Italian Operations Research Societies，2008，6(2):125-142.

[6]ACHTERBERG T，KOCH T，MARTIN A.Branching rules revisited[J].Operations Research Letters，2005，33(1):42-54.

[7]FRIBERG D.An implementation of the branch-and price algorithm applied to opportunistic maintenance planning[D].Gothenburg:University of Gothenburg，2015.