数学教师对学生学业成就的影响研究

王立东，曹一鸣，郭 衎

(1.北京师范大学中国基础教育质量监测协同创新中心，北京 100875；2.3.北京师范大学数学科学学院，北京 100875)

一、问题的提出

常识告诉我们：优秀教师可以帮助学生获得更高的学业成就。但是，教师到底如何影响的学生学业成就，却缺乏量化的数据佐证。进入20世纪，学界开始尝试使用量化研究方法，基于大样本数据，深入细致地分析教师对于学生学业成就的影响。[1]

许多不同学科背景的学者基于不同的视角对于这个主题进行了探讨。

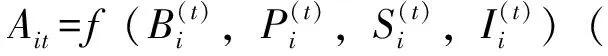
Dunkin和Biddle提出了四组变量系统，后来成为这类研究的基本话语系统：(1)前变量(Presage)：教师特征、经验、培训以及其他影响教学行为的特征变量；(2)背景变量(context)：学生、学校、社区以及班级等特征变量；(3)过程变量(process)：教师、学生的可观察的行为变量；(4)结果变量(product)：反映智力因素和非智力因素等方面的变化的变量。[4]Koehler和Grouws进一步明确了这个话语系统的结构框架，[5]如图1。教师前变量(如教龄)通过教师过程变量(如课堂教学行为)与学生发生作用，影响学生的数学学习(包括认知方面与非认知方面)。

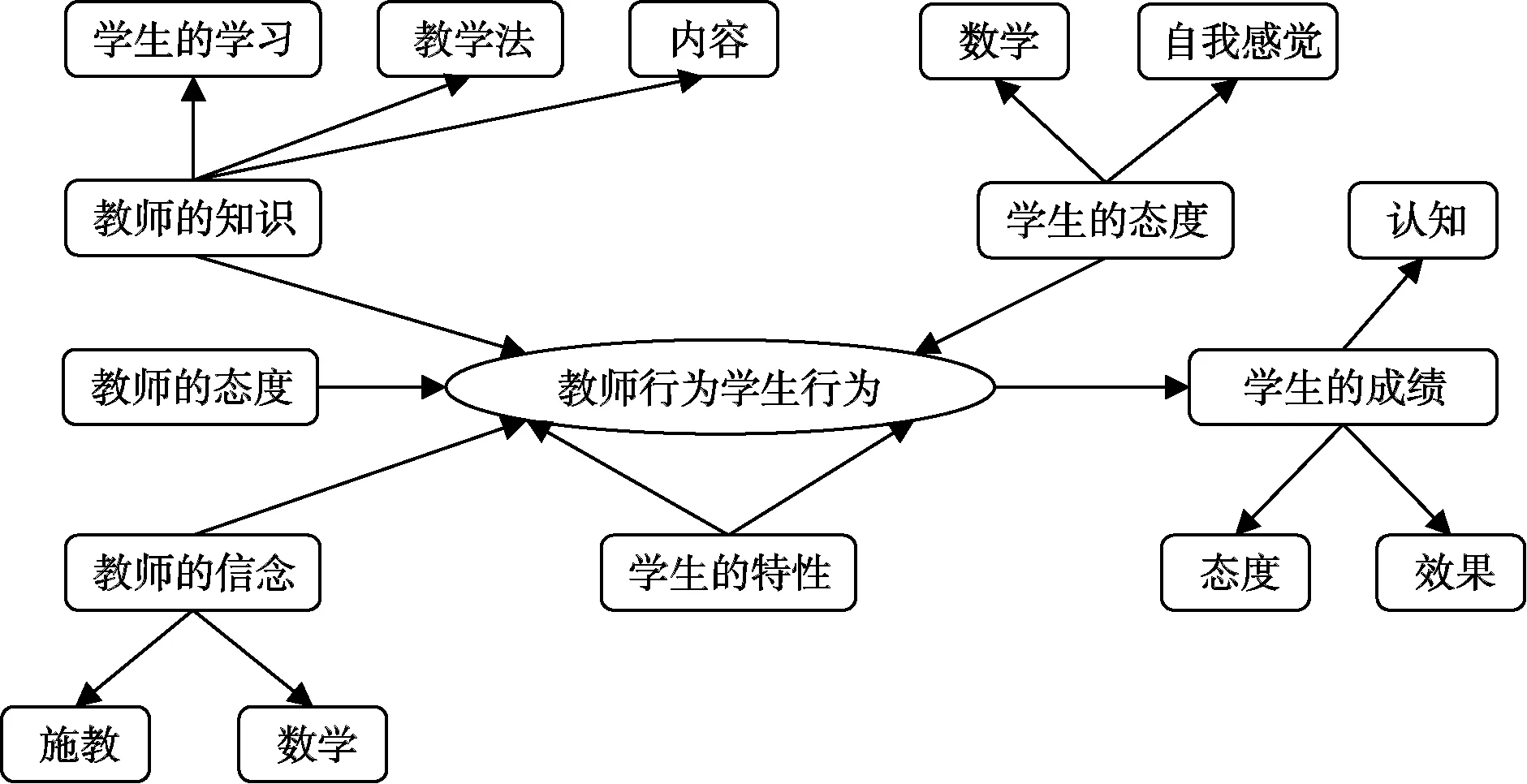
图1 Koehler & Grouws研究的框架结构

以Coleman报告为代表的研究视角通常称为教育生产函数研究，研究者主要为教育经济与政策领域的学者。倾向于从宏观的视角(政策层面)，[6]探讨教师作为一种资源投入，经过一定的教育过程后，取得什么样的教育成果产出(如：高学历教师是否更能够帮助学生提高成绩的问题[7])。研究者重视以研究成果为依据指导有关的教育政策决策 (如：是否投入资金聘任更多的高学历教师等)。

以Dunkin和Biddle模型为代表的研究视角通常称为过程—结果研究(process-product)或前变量—结果研究(presage-product)，研究者主要为教学或教育心理领域的学者。倾向于从微观的视角(课堂层面)，[8]探讨知识水平、课堂教学实践等教师特征与学生学业成就的关系(如：是否教师的PCK水平越高，学生成绩就越好[9])，研究者重视以此为依据，完善教育教学理论，指导教师的职前教育与职后培训(是否需要在教师教育中强化PCK的内容)等。

上世纪八十年代以来，不同视角的研究呈现出整合的趋势。[10]从某种意义上讲，教师影响研究是一类可以为多个教育学领域的理论与实践提供依据的基础性研究。虽然关注该主题的研究者在学科背景、研究目的，以及对于研究成果的应用等方面存在较大差异，但从研究者所采用的研究方法(技术路线)与所获得的研究成果上看又有很大的相似度，在很多情况下一个研究成果可以回答多个领域的研究问题。

针对已有的研究成果的局限, Campbell等人提出了教师影响研究的差异性模型(differentiated model)，强调教师效能在不同的背景下可能存在差异(如：教师在不同年级，不同科目，不同学生群体产生的影响不同)。[11]Shavelson，Webb和Burstein提出，用于反映教师影响的学生标准化测验成绩可能存在质量问题(如：单一维度的分数可能不能高效度地反映学生的学业成就)，在此基础上，他们提出新的研究需要应用基于认知心理学和心理测量学方法获得的多维评价结果，以此来代替单一的分数，进而更深入的描述教师影响。[12]

下文将在已有的研究基础上，利用认知诊断方法构建差异性教师影响模型，讨论如下的研究问题：数学教师对学生在不同数学领域、不同认知水平学业成就产生了什么样的差异性影响？

二、研究设计与研究方法

(一)理论模型

在以上理论研究的基础上，本研究提出如下的理论框架。

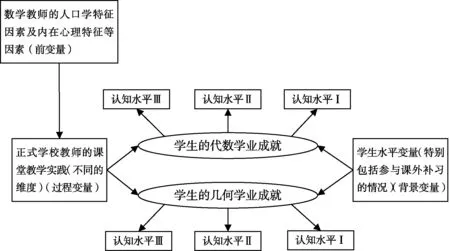
图2 本研究理论框架示意图

我们所关注的是教师的课堂教学对于学生在代数、几何两个基本的数学学习领域的影响。可关注对不同认知水平的学业内容的学习的影响，为此，我们设计了7年级学生数学学业成就的测量模型与教师变量的测量模型，并设计了相应统计模型以估计教师变量对于学生学业成就影响的尺度。

(二)7年级学生数学学业成就的测量模型(认知诊断理论的应用)

如前文所述，Shavelson等人提出教师影响研究的发展应当关注认知诊断理论的应用，[13]Xin，Xu和Tatsuoka[14]基于TIMSS数据，利用认知诊断理论获得了一个多维学生成绩(包括“过程技能”，“阅读技能”和“数学思维技能”的成绩)，进而深入、细致地解析了教师资格证(teacher credential)对于学生数学学习的不同方面的影响，这为后续的研究提供了很好的范本。

数学学习内容具有不同的认知水平(如课程标准中的行为动词要求)，因此数学学业成就的评价也应区分学生在不同认知水平学习内容上的学业成就，即学生的不同认知水平学业成就构成了对于学生数学学习的一个多维评价。应用认知诊断理论，设计了测量学生在不同认知水平学习内容的学业成就的模型，具体的设计如下：

首先，基于由数学教育教学专家筛选出课程标准中的若干条处于核心知识地位的学习内容条目作为测量的基本单元，包括8个代数条目(涉及7年级教学内容的50%)，如：“A1.1 有理数的意义、数轴上的点表示有理数、比较有理数的大小”。11个几何条目(涉及7年级教学内容的50%左右)，如：“G2.2 比较角的大小(能估计一个角的大小，会计算角度的和与差)”。代数与几何是各国教科书中所占比重最大的两个数学内容,[15]代表了数学学习的核心内容。

然后基于一个改进自Stein等[16]， 鲍建生[17]和中华人民共和国教育部[18]等学者与单位的研究成果的认知水平编码系统对于上述条目进行编码：

表1 认知水平编码系统

通过数学内在的逻辑关系组合成如下的层次结构(包括代数和几何两个子测验)：

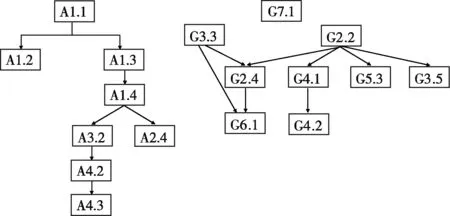
图3 层次结构图

上图中，每个矩形代表一个课标条目，箭头表示学生需要首先掌握一个知识，然后才能掌握下一个知识。上述层次结构构成了测验设计的认知模型，在此基础上，应用认知诊断理论中的属性层次模型(Attribute Hierarchy Method：AHM)设计了相应的测试试卷(卷Ⅰ：代数测试；卷Ⅱ：几何测试)。每个课标条目作为AHM中的一个属性(即测量的基本单元)。

以代数测试为例，我们基于如下的Q矩阵，测试题目共包括11个类型(I1-I11)(正确回答某类题目都需要学生掌握若干个属性，每类1-2个题目)，学生正确回答某类题目所需要掌握的属性(数学知识)由如下Q矩阵给出(1代表回答该类问题需要掌握该属性，0代表不需要)。

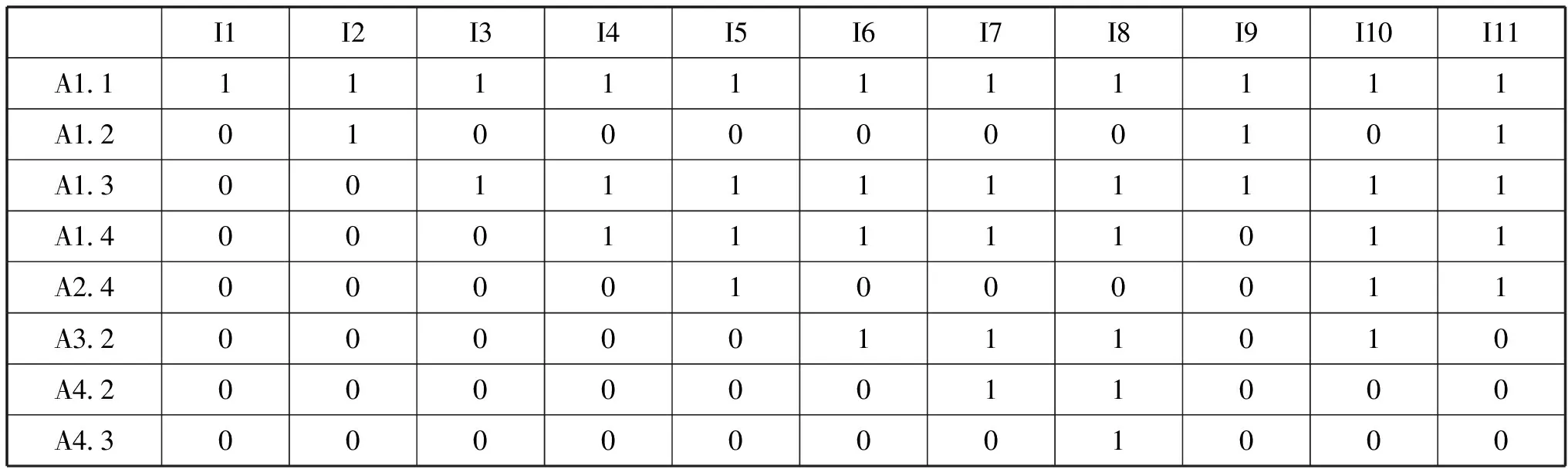
表2 代数测试Q矩阵

利用神经网络模型，[19]可以计算出学生对各个属性的掌握情况的评价(属性掌握分数：用一个定义在[0，1]上的实数来描述)，我们通过取被编码为同一个认知水平的各个属性的属性掌握分数的平均值来获得学生在这个认知水平的学业成就的估计，从而获得一个学生数学学习的多维评价。

(三)教师变量的测量模型(课堂教学行为编码)

教师的课堂教学实践是教师对于学生学业成就的直接影响因素,我们所选择的教师变量主要包括教师课堂教学实践的测量数据(即过程变量)，同时也搜集了部分教师前变量数据(教龄、学历、性别)。本研究利用北京师范大学MIST-CHINA国际合作项目数据库中的课堂录像分析框架。

该分析框架包括如下的三个分析维度和相应的编码系统(包括5个题目0-4分值的题目(Rubric))：(1)数学任务；(2)课堂对话与交互作用(包括教师提问、教师反馈和学生反馈)；(3)教师讲解。

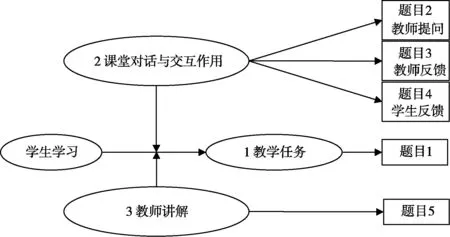
图4 课堂录像分析框架

(四)统计模型

在已有的研究中，多个统计模型被应用过：如(多元)回归模型 (包括方差分解模型(variance decomposition models)，因素分析与路径分析模型(结构方程)，列联分析(卡方检验)等,其中回归模型是主要的统计分析工具。Raudenbush和Bryk质疑简单的回归模型会造成估计的偏差，提出需要应用当时已经得到发展的多水平模型(Multilevel Model)。[20]随着统计理论的进一步发展，特别是统计软件的开发(如HLM系列软件)，使得多水平线性模型(HLM)成为教师影响研究中的主流模型。

本研究将使用2-水平HLM模型来估计教师变量对于学生数学学业成就的影响。模型建构过程如下：

零模型：

Level-1：Y=B0+R

Level-2：B0=G00+U0

其中Y代表学生在某个数学领域(代数、几何)的某个认知水平学习内容上的学业成就的AHM估计结果，B0为学生水平均值，R为学生水平误差，G00为教师水平均值，U0为教师水平误差。

在零模型的基础上，加入学生水平的背景变量：

模型1：

Level-1：Y=B0+B1*(TEXTBOOK)+B2*(ZSCHOOLM)+B3*(SC3)+B4*(SC7)+R

Level-2：B0=G00+U0

B1=G10

B2=G20

B3=G30

B4=G40

我们引入的学生变量主要包括：用来控制学生未被随机地分配到各个学校而引起的随机性问题的学校成就均值变量ZSCHOOLM; 用来控制由于使用不同教科书而带来的随机性问题的教科书变量TEXTBOOK(代表学生使用的两种不同版本的教科书)；SC3代表学生参加课外补习的时间；SC7在一定程度上代表学生的家庭状况(SES)(学生拥有个人电脑情况)。而家庭的社会经济状况是已有研究中，普遍认可和关注的学生水平变量。

仅利用学生的学业成就数据，我们利用方差分解技术计算教师水平对于学生成就方差的解释率(Intra-class Correlation(ICC))，以及d-type 效应量，[21]进而活动对于教师影响尺度的整体估计。

在分析了教师影响的尺度之后，我们加入具体教师水平变量(如教师在课堂教学中使用的数学任务的认知水平：TASKLEVE)，通过这种方式来分析教师影响的结构。

模型2

Level-1:Y=B0+B1*(ZSCHOOLM)+B2*(SC3)+B3*(SC7)+B4*(TEXTBOOK)+R

Level-2:B0=G00+G01*(TASKLEVE)+U0

B1=G10

B2=G20

B3=G30

通过讨论对于G01的估计，以及加入教师变量后的学业成就的方差消减比例来估计该变量对于学业成就的影响(该变量在多大程度上解释了教师影响)。

(五)研究的样本

教师影响研究对于数据的要求较高，如需要教师数据以及与其对应的学生数据，或者是需要多年的纵向数据等。因而获得相应数据所消耗的人力物力资源较多。这使得许多研究因为采用 “方便样本”而受到一定的系统性局限，许多研究变量选择往往是由数据的可得性决定的(如对于TIMSS数据的依赖)，而并非是理论讨论的结果，这使得现有研究往往不够系统性。本研究针对性地搜集了理论框架设计所需数据，从而保证了研究的系统性。数据来自北京师范大学数学科学学院的MIST-CHINA国际合作项目的数据库，样本来自中国3个大城市学区的教师与学生。

用分层随机抽样的方法从重点中学(示范中学)与非重点中学(普通中学)中近似随机选择若干所初级中学。从每所学校的7年级随机选取5-7名数学教师作为教师样本，选取每位教师教授的一个教学班的学生为学生样本(随机选择每位教师的一半的学生完成代数测试，另一半学生完成几何测试)，有效数据为：1304名学生的代数测试数据和课外学习情况调查数据，由63位教师任教(其中包括36位教师的录像分析数据和背景数据，对应610位学生，来自2个学区)，1390名学生的几何测试数据和课外学习情况调查数据，由66位教师任教(其中包括35位教师的录像分析数据和背景数据，对应656名学生，来自2个学区)。

三、数据分析与讨论

按照前文的研究设计，运行模型获得了如下的分析结果：

(一)教师整体影响的估计

通过运行AHM的模型，我们获得学生在代数领域的不同认知水平和几何领域的不同认知水平上的学业成就的估计。这里，由于数据的限制，技术上的将前文所设计的4-水平认知水平模型整合为代数2个水平(低认知水平(整合了LevelⅠ与Level Ⅱ)，高认知水平Level Ⅲ)，几何3个水平(低认知水平(LevelⅠ)，中等认知水平(Level Ⅱ)，高认知水平(Level Ⅲ))。进行这种技术处理是因为我们认为Level Ⅳ的成就不易由纸笔测验测量。此外，对于代数测试，仅包含1个Level Ⅰ属性，不能保证其测量信度，所以整合LevelⅠ和Level Ⅱ两个水平。

模型运行的结果如下：

表3 零模型

表4 模型1

总的来讲，通过控制学生水平变量“提纯”后7年级数学教师影响在代数、几何的各个认知水平上均达到中等或偏上的效应量水平,[22]如对于高认知水平的代数学业成就来说，教师解释了9.8%的学生学业成就的方差(即9.8%的学生学业成就方差是由于任课教师的差异而引起的)，产生了0.31的效应量(教师影响每增长一个标准差，学生成绩增长0.31个标准差)，而与之对应的几何学业成就的结果为方差解释率18.7%与效应量0.43。

通过上表可以看到，教师对于代数成就的影响要明显小于对几何成就的影响。分析这个差异可能来自代数与几何思维方式的差异，不同数学内容可能受到来自教师教学差异的影响程度不同。从实践经验上看，代数内容更加程序化、算法化，因此不同水平教师的教学差异相对较小，进而产生的教师影响差异就相对较小。这个结果为后续的研究提供了方向。

对于不同认知水平的学习内容，教师对于低认知水平学习内容的影响要略高于对于高认知水平学习内容，但同时其影响尺度又大体相当。这个结果反映了高水平的教师可以帮助学生在各个认知水平的学习任务上获得更高的学业成就，特别值得关注的是，即使在如“了解”(水平Ⅰ)这样相对低认知水平的学业成就上(即许多记忆层面的数学学习任务上)，高水平的教师同样会发挥更大的作用。

上述分析从整体上刻画了教师影响的尺度，但正如Konstantopoulos和Sun 所描述的，这类研究无法刻画教师影响的组成。[23]下面的分析将进一步深入研究教师影响的构成，特别是教师的课堂教学行为的作用。

(二)教师变量对于学生学业成就的影响

依次估计前变量(教龄、学历、性别)和过程变量(教师课堂教学)对代数、几何各个认知水平学习内容的影响。

以下仅列出了模型运行结果为具有显著性影响的一类变量。我们仅发现了教师在课堂教学中使用的数学任务的最高认知需求水平对学业成就有显著影响。

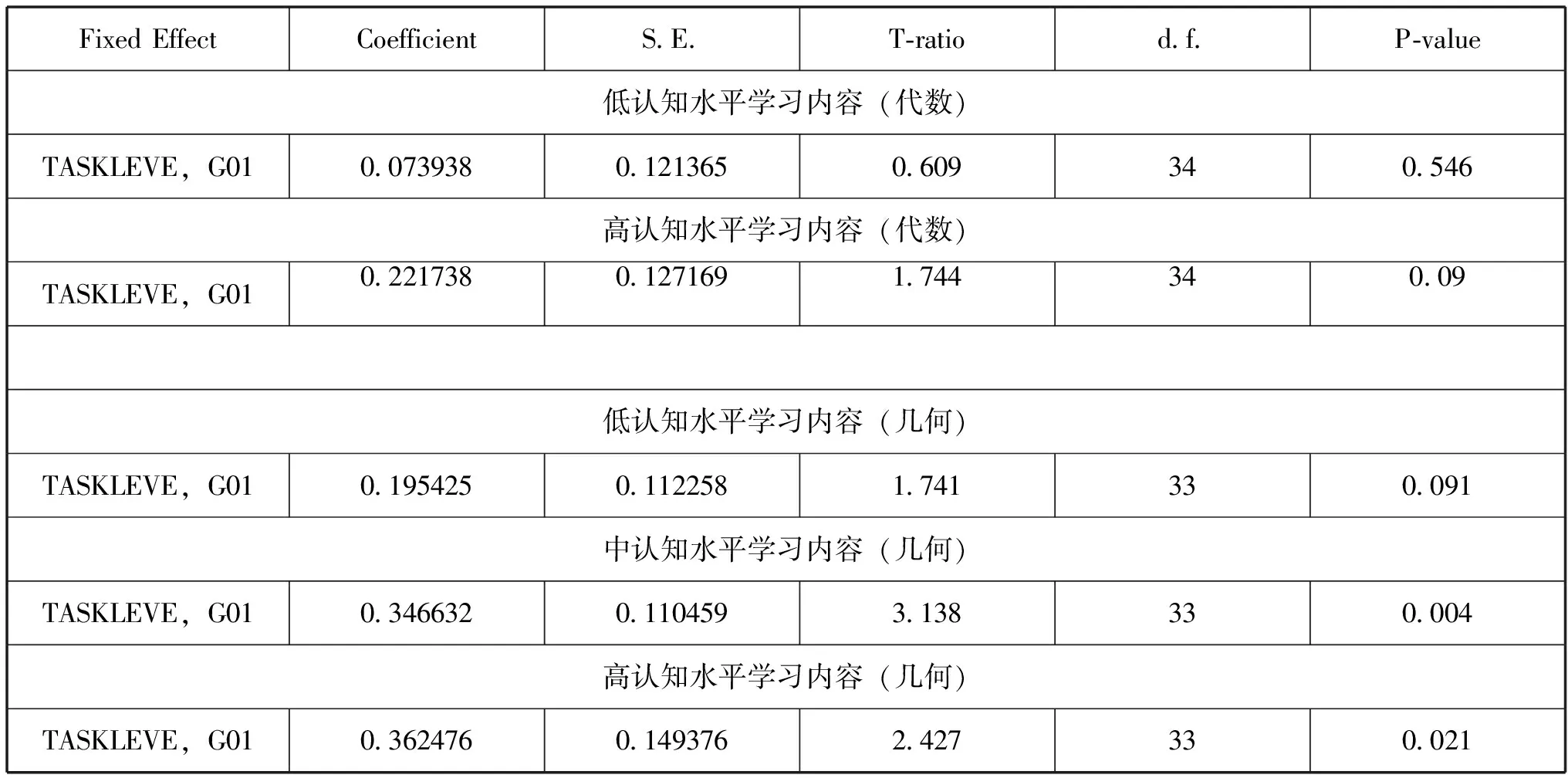
表5 教师变量对学生学业成就的影响

数学任务变量对学生几何成就的影响大于代数影响。对于代数学习，数学任务变量对高认知水平学业成就的影响(0.221738，p=0.090)高于低认知水平的0.073938(p=0.546)。对于几何学习，数学任务变量在三个认知水平上均呈现显著的正向的影响，对高认知水平学业成就的影响高于低认知水平。

从这个结果可以看到，教师在课堂教学中使用高认知需求水平的数学任务对于高认知水平学习内容有重要的意义(特别是几何内容)。

在分析的过程中，曾利用教师课堂教学中认知需求为水平4的任务的比例作为变量。模型的运行结果没有发现显著的影响。因此，数学任务影响的方式可能是不依靠数量，而依靠质量，这在某种程度上说明，单个或少数个高认知需求的数学任务可以在课堂教学中相对长时间的影响了学习活动。[24]

这个结果与著名的Quasar Project 研究结果是一致的，[25]这体现了作为问题解决教学核心的数学任务(特别是高认知需求的数学任务)在课堂教学中长效地为学生提供了参与高认知需求数学活动和数学理解与思维的机会。

本研究特别关注了对不同认知水平学习内容的教师影响。虽然前文对于教师影响的整体分析表明，教师的整体影响在各个认知水平没有明显的差异，但上述对于教师影响的结构性分析表明：数学任务变量对于高认知水平属性成就的影响大于对低认知水平属性成就的影响。对于低认知水平属性成就的影响相对较小(代数：0.073938(p=0.546)，几何：0.195425(p=0.091))，对于高认知水平属性成就的影响较大(代数：0.221738(p=0.090)，几何：0.362476(p=0.021))。这表现出数学课堂教学中使用高认知需求的数学任务的作用域主要集中于高认知水平学习内容上，同时也兼顾了低认知水平学习内容。

本研究也特别关注了不同数学内容领域之间的教师影响的差别，数学任务变量在几何内容的各个认知水平属性上较代数内容解释了更大的教师间差异，同时也具有更大的影响系数。这在某种程度上反映了代数和几何教学与学习的可能的机制差异。当然，应用这个结果需要考虑到的课堂录像数据并非按照内容(代数和几何分类)，因此，在理解这个结论时，要考虑到代数与几何课堂教学的可能差异。

我们未发现其他过程变量对于数学学业成就的直接影响，当然，显然也不能完全否定师生交互作用与教师讲解在课堂教学中的意义，特别是本研究集中于前三个认知水平，没有考察这些变量对于LevelⅣ的影响，以及数学非认知因素的影响(如对于数学的信念、态度、兴趣等)。

我们也未发现被考察的三个前变量(教龄、学历、性别)对于学业成就的直接影响。上述变量对于学业成就可能产生间接影响，如高学历的教师可能倾向于使用高认知需求的数学任务，进而影响学生成就，结构方程模型能够很好的考察这种影响路径，我们将尝试另文分析。

四、结论

(一)教师对于学生在几何的学业成就的影响大于代数

分析这个差异的原因可能与代数、几何这两个数学领域思维方式的差异有关，即不同领域的数学学习可能受到教师水平差异的影响程度不同，相对程序化的代数学习受到不同教师水平差异的影响相对较小。

(二)教师对于学生在了解、理解、掌握三个基础性的认知水平上学业成就的影响显著

研究没有发现教师对于上述三个认知水平的影响尺度的显著差异，这个结果反映了高水平的教师可以帮助学生在各个认知水平的学习任务上获得更高的学业成就，特别值得关注的是，即使在如“了解”这样相对低认知水平的学业成就上，高水平的教师同样发挥了更大的作用。

(三)教师在课堂教学中使用的数学任务的最高认知需求水平起到了重要的作用，较好地解释了教师影响的结构

数据分析表明：认知需求高的数学任务更大地影响了学生在高认知水平上的学业成就(特别是几何内容)。可以认为，高认知需求水平的数学任务促进了学生参与高水平的数学思维活动，促进了其对于高认知水平学习内容的理解(特别是对于几何内容)，体现了教师行为与学生行为的一致性。同时，高认知需求的数学任务在一定程度上也促进了学生对于相对低认知水平教学内容的学习，这体现了高认知需求的数学任务影响了学生各个认知水平的数学学习。

(四)三个前变量(教龄、学历、性别)对于学业成就的直接影响不显著,上述变量对于学业成就可能产生的是间接影响

总的来说，本研究实现了利用认知诊断方法构建差异性教师影响模型的目的，较为全面地描述并部分解释了教师对于学生学业成就的影响，在此基础上，可以进一步深入的讨论教师影响，如基于结构方程模型的间接影响研究，纵向研究，针对高级思维和创造力的研究和非认知因素的研究等。

[1]王立东.数学教师对学生学业成就的影响研究[D].北京：北京师范大学，2012: 1.

[2] Coleman, J.S.Equalityandachievementineducation[M]. Boulder, CO: Westview Press, 1990:3-5.

[3] Hanushek，A.E. The Economics of Schooling: Production and Efficiency in Public Schools[J].JournalofEconomicLiterature，1986，24(3):1151.

[4] Dunkin, M., Biddle, B.Thestudyofteaching[M]. New York: Holt, Rhinehart & Winston, 1974:35.

[5] Koebler, M.,Grouws, D.A.MathematicsTeachingPracticesandTheireffects[M]//Grouws,D.A.Handbook of Research on Mathematics Teaching and Learning.New York: Macmillan Publishing Company,1992:289-290.

[6] 王立东,曹一鸣.教师对学生数学学业成就的影响研究述评[J].数学教育学报,2014,23(3) :48.

[7] Wayne, A.J., Youngs, P. Teacher Characteristics and Student Achievement Gains: A Review[J].ReviewofEducationalResearch, 2003,73(1): 89.

[8] Dunkin, M., Biddle, B.Thestudyofteaching[M]. New York: Holt, Rhinehart & Winston, 1974:37.

[9] Hill, H., Rowan, B., Ball, D. Effects of Teachers’ Mathematical Knowledge [J].AmericanEducationalResearchJournal, 2005,2(2):371.

[10]王立东,曹一鸣.教师对学生数学学业成就的影响研究述评[J].数学教育学报,2014，23(3):49.

[11] Campbell, R.J., Kyriakides, L., Muijs, R.D. et al. Differential teacher effectiveness: Towards a model for research and teacher appraisal [J].OxfordReviewofEducation, 2003,29(3): 347.

[12] Shavelson, R.J.,Webb, N.M.,Burstein, L.MeasurementofTeaching[M]//Wittrock, M.C.Handbook of research on teaching (Third Edition).New York: Macmillan,1986:1117.

[13] Shavelson, R.J.,Webb, N.M.,Burstein, L.MeasurementofTeaching[M]// Wittrock, M.C.Handbook of research on teaching (Third Edition).New York: Macmillan,1986:1120.

[14] Xin, T., Xu, Z.,Tatsuoka, K. Linkage between teacher quality, student achievement, and cognitive skills: A rule-space model [J].StudiesinEducationalEvaluation, 2004，30:205.

[15]吴立宝,曹一鸣.初中数学课程内容分布的国际比较研究[J].教育学报,2013(4):29.

[16] Stein, K.M., Grover, W.B., Henningsen, M. Building Student Capacity for Mathematical Thinking and Reasoning: An Analysis of Mathematical Tasks Used in Reform Classrooms[J].AmericanEducationalResearchJournal, 1996,33(2): 466.

[17] 鲍建生.中英数学课程综合难度的比较研究[M].南宁：广西教育出版社，2009: 5.

[18] 中华人民共和国教育部.全日制义务教育数学课程标准：实验稿[M].北京：北京师范大学出版社,2001:18-19.

[19] 王立东, 郭衎, 孟梦. 认知诊断理论在数学教育评价中的应用[J]. 数学教育学报, 2016, 25(6):16.

[20] Raudenbush, S.W.,Bryk, A.S. A hierarchical model of studying school effects [J].SociologyofEducation, 1986,59(1):1.

[21] Rowan, B., Correnti, R.,Miller, R.J. What large-scale survey research tells us about teacher effects on student achievement: Insights from the Prospects Study of elementary schools [J].TeachersCollegeRecord, 2002,104(8):1525-1526.

[22] Rowan, B., Correnti, R.,Miller, R.J. What large-scale survey research tells us about teacher effects on student achievement: Insights from the Prospects Study of elementary schools [J].TeachersCollegeRecord, 2002,104(8): 1533.

[23] Konstantopoulos, S., Sun, M.Is the Persistence of Teacher Effects in Early Grades Larger for Lower-Performing Students?[J].AmericanJournalofEducation,2012,34:320.

[24] Doyle, W. Academic Work[J].ReviewofEducationResearch,1983,53 (2):160-161.

[25] Silver, E.A., Stein, M.K. The Quasar Project: The “Revolution of the Possible” in Mathematics Instructional Reform in Urban Middle Schools [J].UrbanEducation, 1996,30:476.