考虑堆载时间效应的排桩水平承载力研究

竺明星，龚维明，卢红前，王磊，王磊

（1.中国能源建设集团江苏省电力设计院有限公司，江苏 南京 211102；2.东南大学土木工程学院，江苏 南京 210096）

0 引言

随着我国基础建设的不断发展，不平衡堆载现象普遍存在于路堤、桥梁、港口、厂区建设等工程中。诸多学者分别开展了模型试验[1-2]、数值模拟[3]等研究，分析了堆载作用对邻近基桩承载力的影响。竺明星等[4-5]开展了堆载作用下组合受荷桩承载特性的室内模型试验研究。然而上述研究成果只能反映特定堆载情况下定性规律，不能为工程设计提供理论依据。

基于位移法原理，Poulos[6]采用有限差分法、Liang[7]等采用幂级数法求解了不同土体水平位移模式下的基桩内力半解析解。然而，基于位移法的理论在排桩计算时不能考虑土拱效应影响。基于压力法原理，竺明星等[8]采用传递矩阵法分别解得考虑组合荷载作用下被动桩桩身响应解。但这些理论无法考虑软土地基堆载时间效应的影响。朱中发[9]等开展了不平衡堆载长期原位试验研究，但未能提出相应的计算理论。总体而言，考虑不平衡堆载时间效应的邻近被动桩承载特性研究文献相对较少且研究进展缓慢。

本文首先建立堆载短期作用、堆载长期作用下桩身被动荷载分布表达式。随后引入负摩阻力作用并结合传递矩阵法解得组合受荷被动桩桩身响应半解析解。通过与工程案例对比验证本文理论的可靠性。最后，开展临界桩间距参数影响分析。

1 考虑时间效应的堆载作用分析

1.1 桩身被动荷载求解

Ito等[10]基于局部塑性变形理论求解了桩身被动荷载，但该理论不能考虑堆载的时间效应。Oztoprak[11]在长期堆载监测时发现：堆载初期的土体应力状态接近主动土压力状态；随着时间的推移，土体应力状态最终趋向于静止土压力状态。在此基础上，本文推导得出考虑堆载时间效应的桩身被动荷载计算表达式。

如图1所示，将BB′边等分为mB份，根据竺明星[12]方法计算BB′边每点上水平附加应力为ps（i），则 BB′边上水平附加应力平均值为：

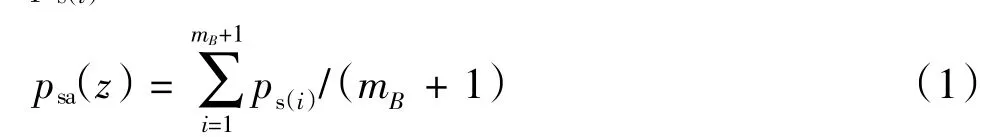
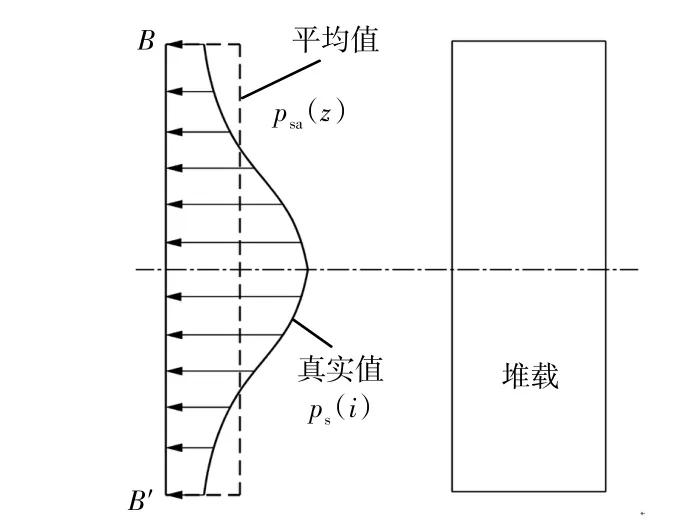
图1 附加应力平均值计算Fig.1 Average value calculation of additional stress

由此可知堆载作用下某一深度处的BB′边（如图2所示）的总水平应力按下式计算：

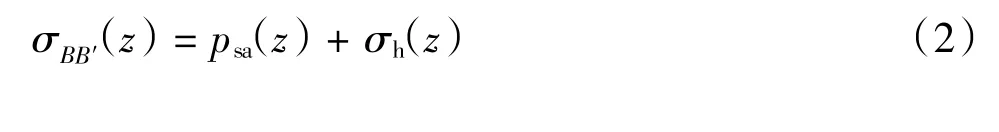
式中：σh（z）为土体自重产生的水平应力，根据Oztoprak等[11]结论，当短期作用时采用主动土压力状态，当长期作用时采用静止土压力状态。赵健[13]根据大量试验，得到了堆载下软土的黏聚力和内摩擦角随固结度的变化规律：

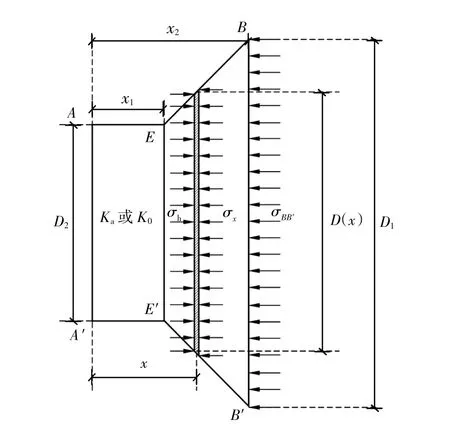
图2 BEE′B′区域微单元体示意图Fig.2 Sketch of micro-element in BEE′B′region

式中：U为固结度；cc和φc分别为堆载作用下不同固结度时的土体黏聚力与内摩擦角。

如图2，根据竺明星[8，12]方法推导得局部塑性变形区域BEE′B′中任意位置处土体水平应力σx为：

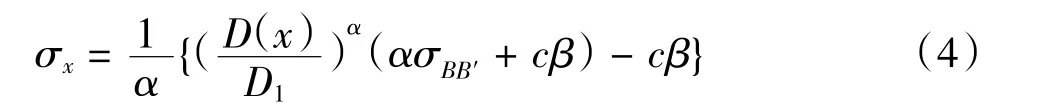
式中：α =Nφ+Nφ1/2tan φ -1；β =2Nφ1/2+Nφ-1/2+2tanφ；Nφ=tan2（π/4+φ/2）；D（x）=D2+2（x-x1）·tan（π/4+ φ/2），为 BEE′B′区域 x∈[x1，x2]位置处竖向长度；x1和 x2分别为（D1-D2）tan（π/8+φ/4）/2和（D1-D2）[tan（π/8+ φ/4）+tan（π/4- φ/2）]/2；D1为桩间距；D2为桩间净距。

由于σBB′（z）向土体流动方向传递过程中应力水平逐渐衰减。因此桩身被动荷载q（z）按下述方式计算：

1）如果BEE′B′区域某个位置x处土体水平应力σx等于土体自重产生的水平应力σh，则可得：

式中：q（z）即为任意深度处桩身被动荷载，kN/m。

2）当第1步条件不成立时，则q（z）为：

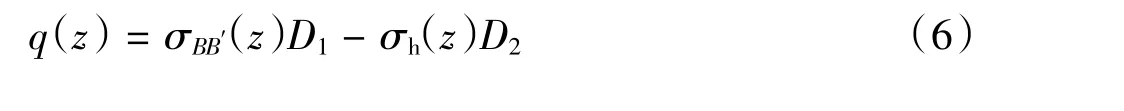
上述计算过程中如果考虑堆载短期作用，则地基土体的黏聚力c和内摩擦角φ取原始值；如果考虑长期作用，则根据公式（3）中的cc和φc值代替c和φ值。

1.2 合理临界桩间距确定

对于隔离桩等一类的主动防护型被动桩而言，合理桩间距的确定是至关重要的。本文提出以堆载产生的水平应力作用经过土拱AEBB′E′A′区域隔离削弱后在AA′边应力与土体自重产生的水平应力相等的合理桩间距确定原则可得：

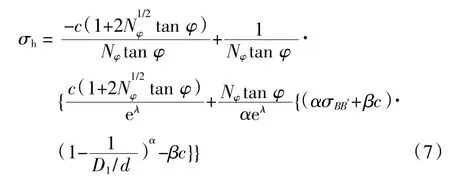
式中：λ=Nφtan（π/8+φ/4）tanφ/（D1/d-1）；d=D1-D2为桩径，D1/d即为所需求解的桩间距比值。

本文提出以沿深度计算所得临界桩间距比值D1/d最小值作为该条件下被动桩临界桩间距（D1/d）crit，则考虑堆载短期、长期作用下临界桩间距比值（D1/d）crit分别定义为（D1/d）low和（D1/d）upper。

2 组合受荷被动基桩承载力半解析解

设桩总长为L的桩嵌入n层地基土中，第i层土中桩的长度、直径和抗弯刚度分别为Hi、di和EIi。桩顶分别作用水平力Ft和弯矩Mt。桩身作用被动分布荷载q（z）。堆载负摩阻力产生的桩身轴向荷载为 V（z）。

2.1 地面下弹性阶段桩身传递矩阵系数求解

图3所示为任意第i层地基土中桩身示意图，该段桩进行mi份等分后每小段长度hi=Hi/mi，则可得：

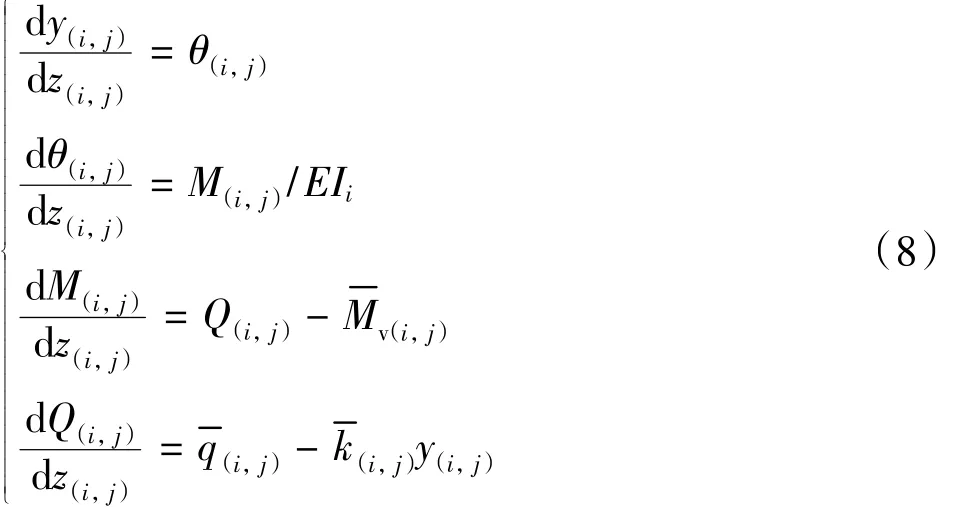
式中：y（i，j）、θ（i，j）、M（i，j）和 Q（i，j）分别为处于弹性阶段的第i层桩中第j小段桩（等分数量为mi）的桩端位移、转角、弯矩和剪力。为第 i层桩中第 j

小段桩的桩身竖向轴力荷载产生的附加弯矩平均值：

式中：Mv（i，j-1）和 Mv（i，j）分别为第 i层桩中第 j小段桩顶部与底部位置处桩身竖向荷载产生的附加弯矩值，其中 Mv（i，j）=V（i，j）θ（i，j），V（i，j）为该截面位置处桩身轴向荷载。

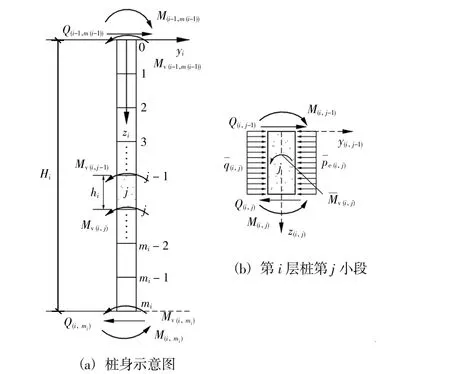
图3 弹性阶段桩离散示意图Fig.3 Sketch of discretization of pile-soil in elastic state

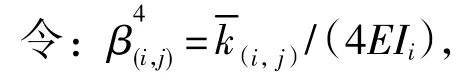
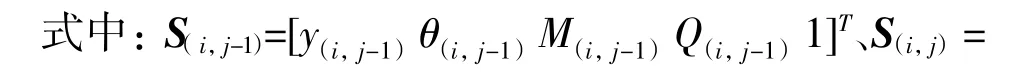
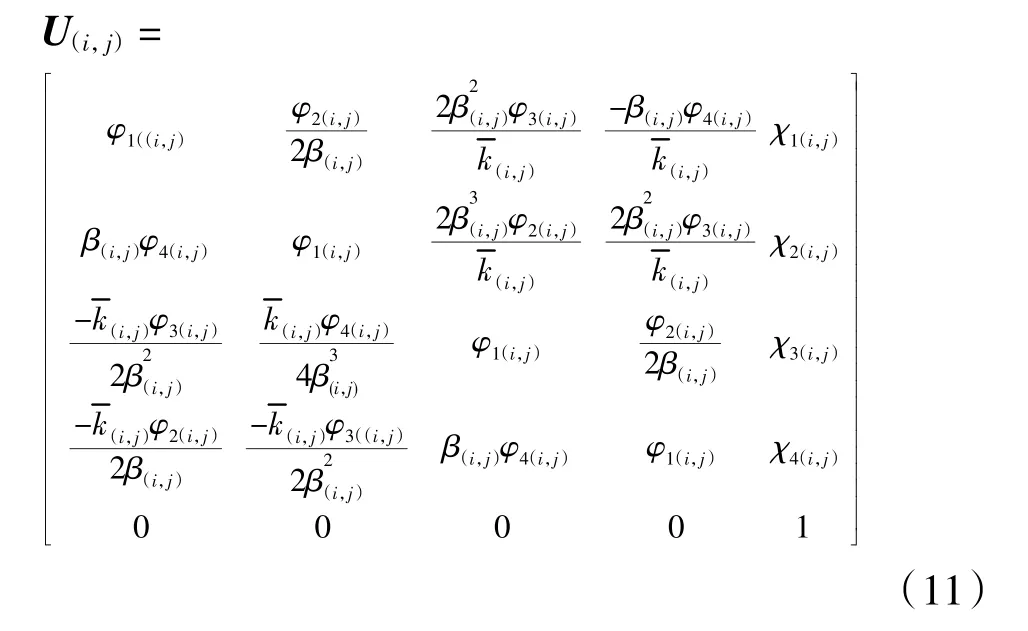
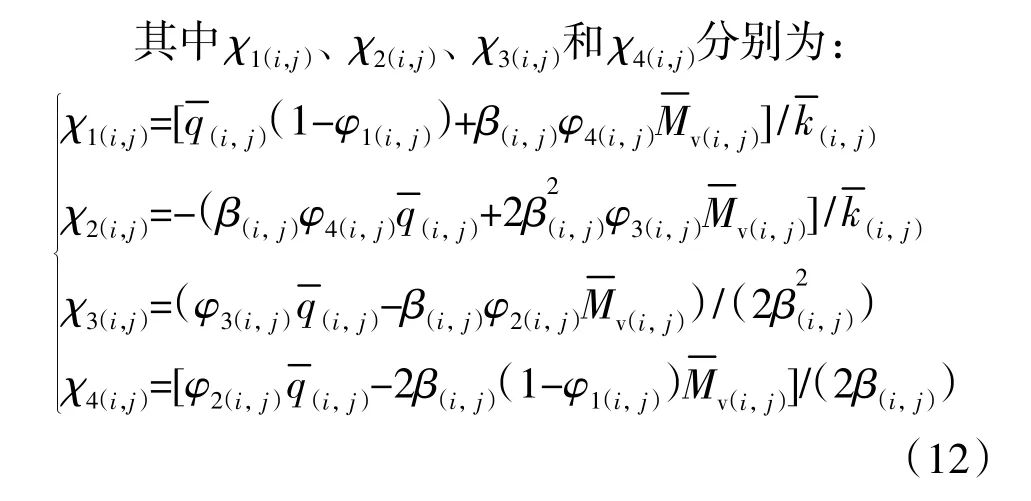
式（11）和（12）中：φ1（i，j）、φ2（i，j）、φ3（i，j）、φ4（i，j）详见文献 [12]所述。通过与文献 [8，12]对比发现，本文所推导的公式（11）克服了文献[8，12]中竖向荷载不能为0的缺陷。

2.2 地面下塑性阶段桩身传递矩阵系数求解

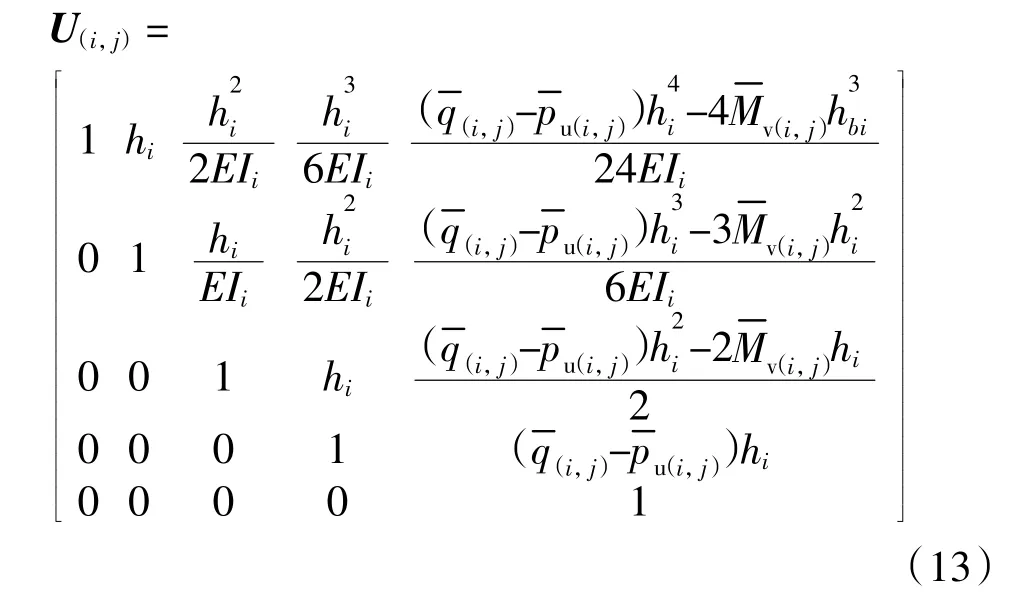
本文所推导的考虑桩身竖向荷载影响的塑性段传递矩阵系数解析解（如公式（13）所示）克服了文献[8，12]中竖向荷载不能为0的缺陷。

2.3 桩身响应迭代求解过程

根据传递矩阵法原理，结合公式（10）、（11）和（13）可得整个桩身的传递矩阵方程为：

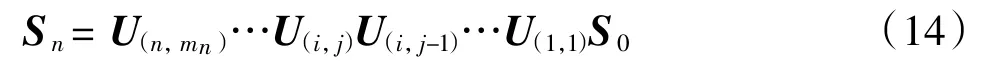
其中：Sn=[ynθnMnQn1]T和 S0=[y0θ0M0Q01]T分别为整个桩的桩端和桩顶处变形、转角、弯矩和剪力的状态矩阵向量；U（i，j）为桩身传递矩阵系数，当桩侧土体为弹性状态时采用公式（11）计算，当桩侧土体为塑性状态时采用公式（13）计算。

常见的桩顶和桩端初始边界条件如下：

将公式（15）和（16）中对应的边界值代入方程（14）即可解得桩顶状态向量S0，则任意位置处的桩身响应为：

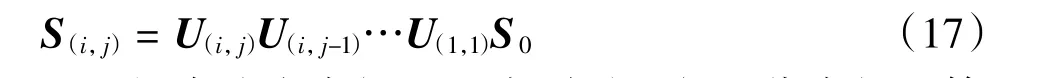
桩身响应求解过程中则需进行迭代求解。第1 次迭代计算时假定任意截面处 Mv（i，j）值均为 0。

3 工程案例验证

某桥梁工程开展了吹填区试验值现场不平衡堆载原位试验，如图4所示，该工程相关参数详见文献[12]。

图4 原位堆载试验示意图（m）Fig.4 Sketch of in-situ surcharge load test（m）

堆载长期作用时需考虑桩侧负摩阻力影响，则中间桩桩身轴力分布[14]近似为：

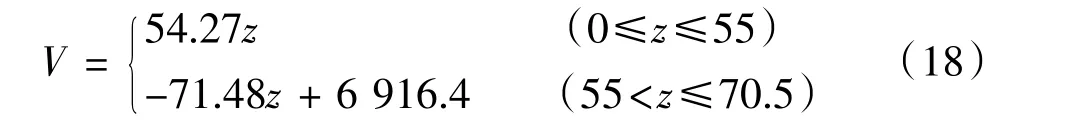
3.1 中间桩（SZ2）桩身响应分析

如图5（a）所示，本文提出的堆载短期作用下桩身变形与第7天、第10天实测规律几乎吻合，误差分别为3.24%和1.08%，验证了本文堆载短期作用计算理论的合理可靠性。

本文堆载长期理论变形值与第44天、第74天实测值相比误差分别为1.6%和5.79%，误差很小。但趋势很明显，即，随着时间的增加，实测桩身变形在增加；特别是当第723天最后一次监测时发现中间桩（SZ2桩）的桩顶变形已经达到0.51 m，如图5（b）所示。由JGJ 94—2008《建筑桩基技术规范》[15]可知桩身裂缝限值wlim为0.2～0.3mm。由GB 50010—2010《混凝土结构设计规范》[16]裂缝计算公式可得桩身裂缝限值wlim范围内所对应的桩身最大弯矩如图6（a）所示。由图6（b）可知，当堆载长期作用时，桩身最大弯矩为2 280.02 kN·m，此时桩身裂缝值为0.375 mm，已经超过裂缝允许值的上限值，此时桩身已经破坏。因此从第44天开始桩身已经开始破坏，随着裂缝增加，桩身破坏程度越来越严重。

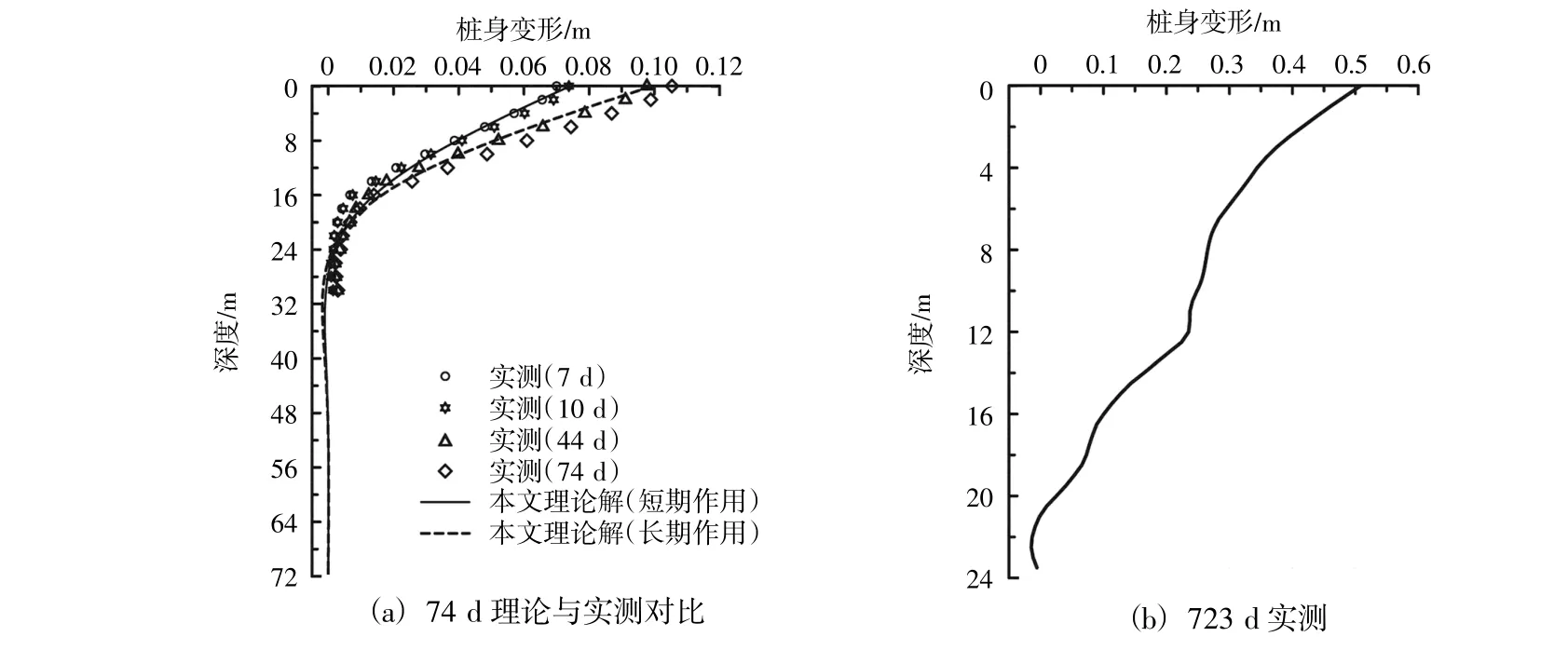
图5 桩身变形对比Fig.5 Comparison of pile deflection

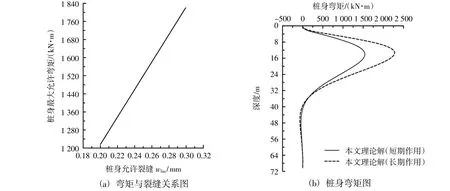
图6 桩身弯矩图Fig.6 Bending moment of pile

3.2 边桩（SZ1）桩身响应分析

如图4所示，对3根试验桩而言，边桩（SZ1）受力状态与中间桩（SZ2）明显不一样，边桩只存在单侧土拱效应，因此，本文桩身被动荷载理论不能直接应用于边桩。通过大量试算对比分析可得：对堆载短期作用而言，取中间桩被动荷载的0.55倍作为边桩桩身被动荷载；对堆载长期作用而言，取中间桩被动荷载的0.67倍作为边桩桩身被动荷载，则根据这一结论计算所得结果与实测值对比如图7所示。

3.3 负摩阻力对桩身响应影响分析

堆载长期作用下桩身负摩阻力对桩身产生下拉力如公式（18）所示。从图8中可知与不考虑负摩阻力影响相比，考虑负摩阻力影响时最大变形误差为0.7%、最大弯矩误差为0.79%。由此可知堆载产生的负摩阻力对被动桩桩身水平承载特性的影响可以忽略不计。

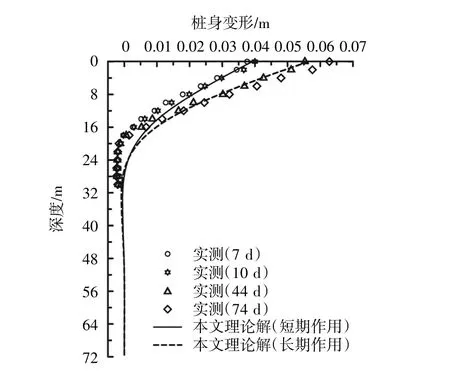
图7 SZ1桩的桩身变形Fig.7 Deflection for SZ1 pile

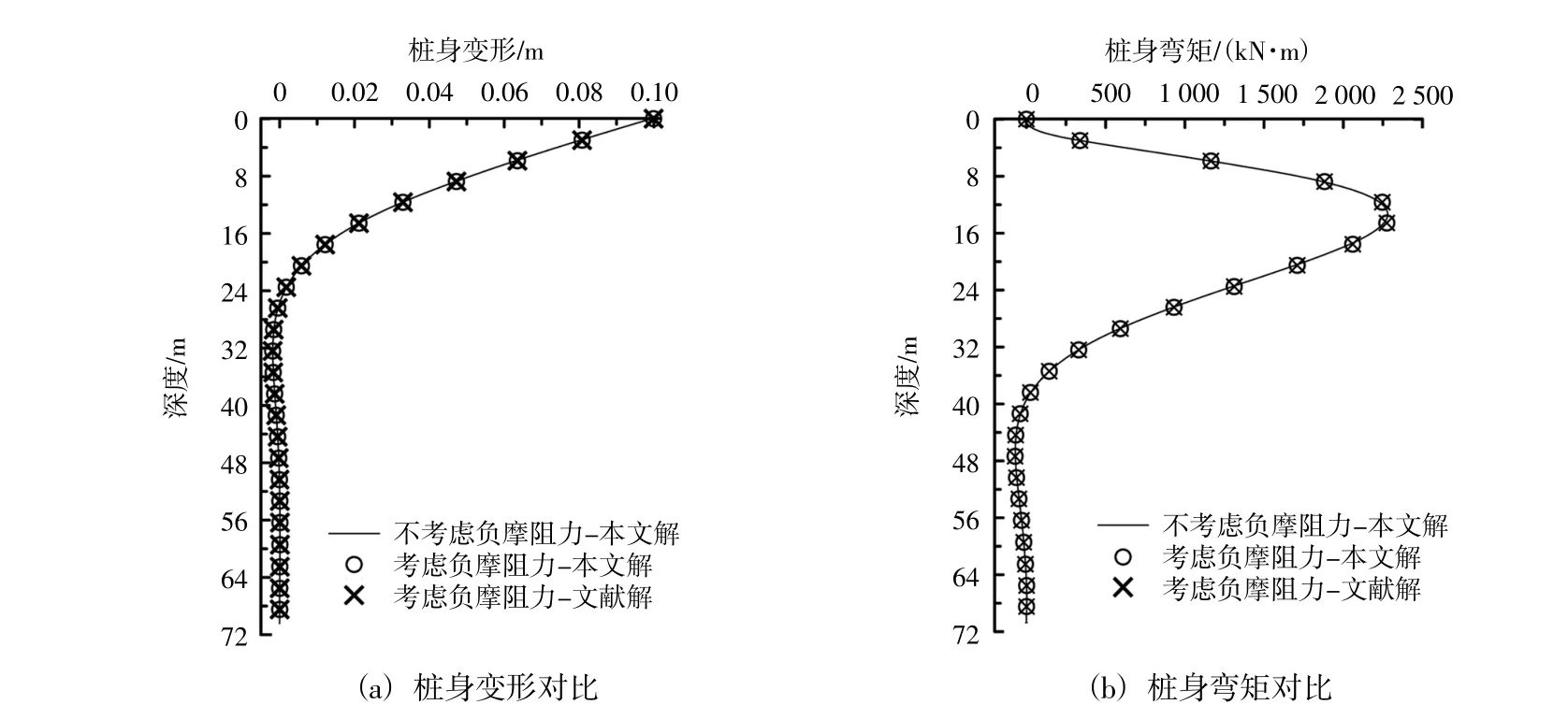
图8 负摩阻力影响分析Fig.8 Influence analysisof negative frictional resistance

4 临界桩间距（D1/d）crit参数影响分析

为研究临界桩间距（D1/d）crit的影响规律，如图9所示，设条形均布荷载宽度b=40 m，堆载边缘距离桩边缘的距离a=2 m，计算深度为30 m；荷载p=100 kPa；重度为γ=20 kN/m3，黏聚力c=20 kPa，内摩擦角 φ =25°。

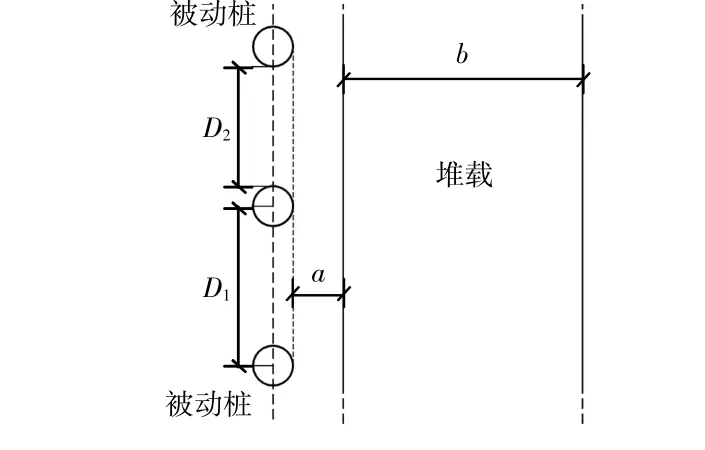
图9 堆载示意图Fig.9 Sketch of surcharge loading

4.1 堆载荷载大小影响分析

图10 临界桩间距与堆载荷载关系Fig.10 Relation between critical pile spacing and surcharge load

设堆载荷载p范围为20～100 kPa。由图10可知临界桩间距（D1/d）crit均随着堆载荷载的增加而呈非线性减小趋势。临界桩间距（D1/d）crit合理范围应该介于（D1/d）low和（D1/d）upper之间。

4.2 黏聚力大小影响分析

设黏聚力c变化范围为5～55 kPa。从图11中可看出临界桩间距（D1/d）crit均随着黏聚力c的增加而呈线性增加趋势。该规律反映的是随着土体黏聚力c增加，桩间土体的土拱效应增强，进而使得在桩间距D1/d较大时依然能够形成强土拱。

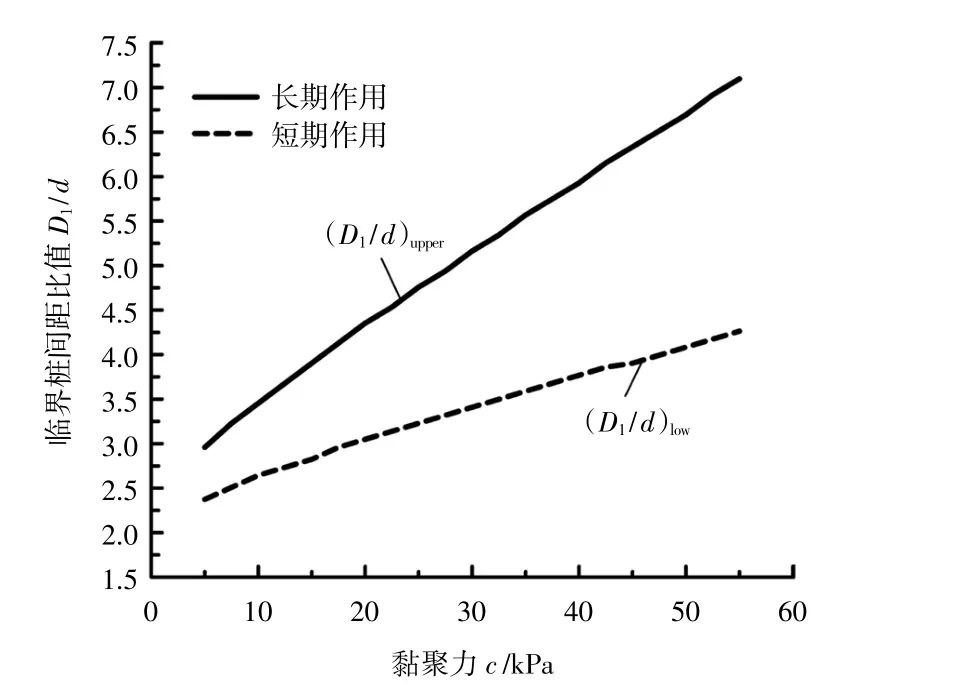
图11 临界桩间距与黏聚力关系Fig.11 Relation between critical pile spacing and cohesion

4.3 内摩擦角大小影响分析

设内摩擦角φ变化范围为5°～55°。其余参数保持不变。从图12中可以看出不论是考虑堆载短期作用还是考虑堆载长期作用，（D1/d）low和（D1/d）upper均随着内摩擦角φ的增加而呈非线性增加，且增加的幅度越来越大。对比图11可知内摩擦角φ影响更加敏感。

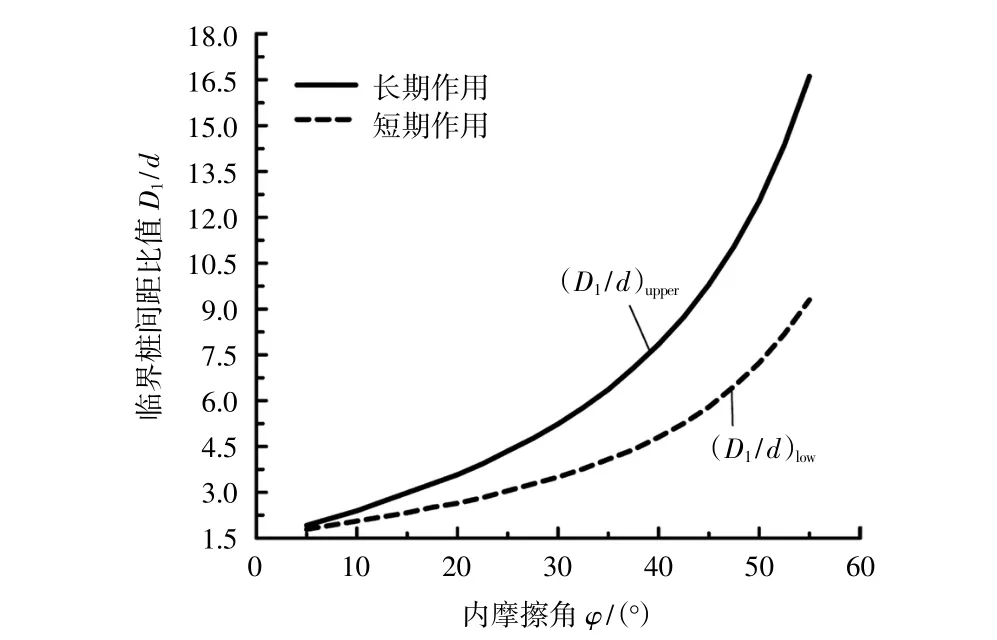
图12 临界桩间距与内摩擦角关系Fig.12 Relation between critical pile spacing and internal friction angle

5 结语

在局部塑性变形理论基础上，本文推导得出考虑堆载时间效应的桩身被动荷载及桩身响应解，通过案例对比分析证明了本文解的正确性，并开展了参数影响分析，得出以下结论：

1）本文解克服了传统方法解中桩身竖向荷载不能等于0的局限性，因此本文解更具有通用性。

2）对于边桩的桩身被动荷载采用经验方法计算：对堆载短期作用而言，取中间桩被动荷载的0.55倍；对长期作用而言，取中间桩被动荷载的0.67倍。

3）临界桩间距（D1/d）crit合理范围应介于（D1/d）low和（D1/d）upper之间；而（D1/d）low和（D1/d）upper均随着堆载荷载的减小、黏聚力和内摩擦角的增加而增加。

4）堆载产生的负摩阻力对被动桩水平承载特性的影响可以忽略不计。

[1] SPRINGMAN S M.Lateral loading on piles due to simulated embankment construction[D].London:University of Cambridge,1989.

[2]CHENLT,POULOSHG,Hull TS.Model testson pilegroupssubjected tolateral soil movement[J].Journal of the Japanese Geotechnical Society Soils&Foundation,1997,37(1):1-12.

[3] HARA T,YU Y Z,UGAI K.Behaviour of piled bridge abutments onsoftground:adesignmethod proposal based on2Delasto-plasticconsolidation coupled FEM[J].Computers and Geotechnics,2004,31(4):339-355.

[4] 竺明星，王磊，龚维明.边载作用下隔离桩隔离效果的影响因素研究[J].岩土工程学报，2014，36（4）：671–679.ZHUMing-xing,WANGLei,GONGWei-ming.Factorsinfluencing isolation effects of isolation piles under side loading[J].Chinese Journal of Geotechnical Engineering,2014,36(4):671-679.

[5] GHEE E H.The behaviour of axially loaded piles subjected to lateral soil movements[D].Nathan:Griffith University,2009.

[6] POULOSH G.Behavior of laterally loaded piles:I-Single piles[J].Journal of Soil Mechanics and Foundations Division,1971,97(SM5):711-731.

[7] LIANG F Y,YU F,HAN J.A simplified analytical method for response of an axially loaded pile group subjected to lateral soil movement[J].KSCE Journal of Civil Engineering,2013,17(2):368-376.

[8] 竺明星，龚维明，何小元，等.堆载作用下考虑土拱效应的被动桩变形内力半解析解[J].岩土工程学报.2013.35（11）：1 997–2 008.ZHU Ming-xing,GONG Wei-ming,HE Xiao-yuan,et al.Semianalytical solution todeformation and internal forceof passive piles under surcharge loads considering soil arching effect[J].Chinese Journal of Geotechnical Engineering,2013.35(11):1 997-2 008.

[9]朱中发.新吹填区对已建桥梁桩基的作用机理研究[D].南京：东南大学，2014.ZHU Zhong-fa.The mechanism of bridge pile by imbanlance surcharge load of new reclamation area[D].Nanjing:Southeast University,2014.

[10]ITO T,MATSUI T.Methods to estimate lateral force acting on stabilizingpiles[J].Soilsand Foundations,1975,15(4):43-59.

[11]OZTOPRAK S,CINICIOGLU S F.Soil behaviour through field instrumentation[J].Canadian Geotechnical Journal,2005,42(2):475-490.

[12]竺明星.组合荷载作用下被动桩承载机理研究[D].南京：东南大学，2016.ZHU Ming-xing.Research on bearing mechanism of passive pile under combined loads[D].Nanjing:Southeast University,2016.

[13]赵健.软土地基强度试验研究及其增长计算理论[D].长沙：中南大学，2010.ZHAO Jian.Research on strength test and strength increasing calculation theory of soft soil foundation[D].Changsha:Central South University,2010.

[14]徐晓.不平衡堆载对桥梁桩基的影响[D].南京：东南大学，2015.XU Xiao.Influence of imbalanced surcharge load of new reclamationareaonbridgepilefoundation[D].Nanjing:Southeast University,2015.

[15]JGJ94—2008，建筑桩基技术规范[S].JGJ94—2008，Technical codefor buildingpilefoundations[S].

[16]GB 50010—2010，混凝土结构设计规范[S].GB 50010—2010,Codefor design of concretestructures[S].