小波降噪及EMD方法在泵房前池水位波动分析中的应用

孙运佳，孔丛颖，李泽，丁广佳，韩涛

（中交天津港湾工程研究院有限公司，中国交建海岸工程水动力重点实验室，天津 300222）

0 引言

核电因其经济性、清洁性、高效性等特征成为中国能源的重点发展对象，受日本福岛事故发生影响，其安全性也成为核电发展的关键因素。滨海核电厂多采用岸边式泵房取水方式，以往研究[1-2]表明在泵房前池会出现长周期波动。根据规范[3]要求，泵房前池波高应小于0.5 m，文献[4]提出由于长周期波属于水位缓慢抬升及下降的过程，并不会对泵房取水安全产生较大影响，因此该波动要求可视为对短周期波的要求。泵房前池的水面波动主要受外海波浪绕射及高水位情况下波浪越过防波堤后产生的次生波影响，对工程平面布置及防波堤的堤顶标高较为敏感，因此科学地对泵房前池的波动进行长短周期的划分及统计，对工程的安全性和经济性具有重要意义。

由于实验室仪器受电磁干扰等影响，测试信号中常包含大量白噪声。本文首先通过小波分析对泵房前池的水波信号进行降噪，然后通过经验模态分解（Empirical Mode Decomposition，EMD）方法，对降噪后的信号进行长短周期分解。

1 原理

1.1 小波降噪

小波分析由于具有多分辨率分析的特点，在信号处理领域得到越来越广泛应用。小波降噪是通过将信号的不同成分分解到不同子空间中，选择合适的阈值，对小于该阈值的小波系数进行量化处理，再通过小波逆变换获得降噪后的真实信号。其中影响降噪效果因素较多，包括小波分解层数、小波类型、噪声类型及阈值选取。

1.2 经验模态分解（EMD）

EMD方法克服了信号处理需要“先验”知识的缺陷，具有对非线性非平稳信号的良好适应性。通过对信号的分解可得（具体步骤见文献[5-6]）：

式中：rn为信号的趋势项即残余信号。信号通过EMD分析，可得到频率由大到小的多阶IMF分量，体现了多尺度分析的滤波过程。EMD方法除了自适应地将信号分解特征外，还具有完备性，即把分解后的各IMF分量及残余信号分量通过线性叠加可恢复原信号，这也是本文利用EMD分解长短周期波的基础。

2 方法

在物理模型试验情况下，泵房前池的水面波动较小，采集到的水波信号为含高频噪声的非平稳非线性信号。利用小波降噪原理及EMD方法对含噪信号处理具体流程如下：

1）通过构造叠加高斯白噪声的不规则波，对比不同小波基函数、小波分解层数及阈值情况下的信号降噪效果；

2）选择对不规则波降噪效果最优的小波参数对泵房前池的波动信号进行降噪；

3）利用EMD分解降噪后的波动信号，分解得到N个IMF分量；对前m（m=1，2…）个IMF分量相加后进行波浪统计得到有效周期TmIMF，并与长短周期的界限Thr比较；

4）若TmIMF大于Thr，则将前m-1个分量作为水面波动长短周期划分的IMF分量界限，再分别统计长短周期波浪参数；若TmIMF小于Thr，则返回第3）步，计算前m+1个IMF分量的有效周期；

5）引入信噪比（SNR）及根均方误差（RMSE）对小波参数降噪效果进行评定。

小波降噪及EMD方法对含噪信号处理流程如图1所示。

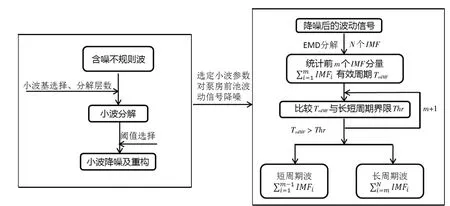
图1 小波降噪及利用EMD方法对泵房前池波动信号处理流程图Fig.1 Flowchart of wavelet de-noising and EMD applied in analyzing the water level fluctuation in forebay of pump station

3 仿真分析

为检验小波降噪的效果，通过对实验室波浪信号与噪声信号的特性分析，利用不规则波叠加高斯白噪声作为实验对象。选取JONSWAP波浪谱模型，构造谱峰周期为8 s，有效波高为3 m，时间为800 s的波浪时序列（见图2（a））。

经实验对比，选取降噪效果较好的db14及sym14进行5层、6层的小波分解，对降噪后的信号进行统计分析，见表1。结果显示，对信号进行6层小波分解后进行降噪得到的各统计波浪参数与原信号的误差很小，除波列最大波高及对应周期相对较大外，其他参数误差均在2%之内；另外由于小波分解5层对信号的降噪程度偏小，其统计的波个数相对误差较大，但对于波列最大波高的估计误差较小，在实际的工程应用中，对波列的最大波高统计可采用降低小波分解的层数来对其进行更为准确的统计。

降噪效果见图2。

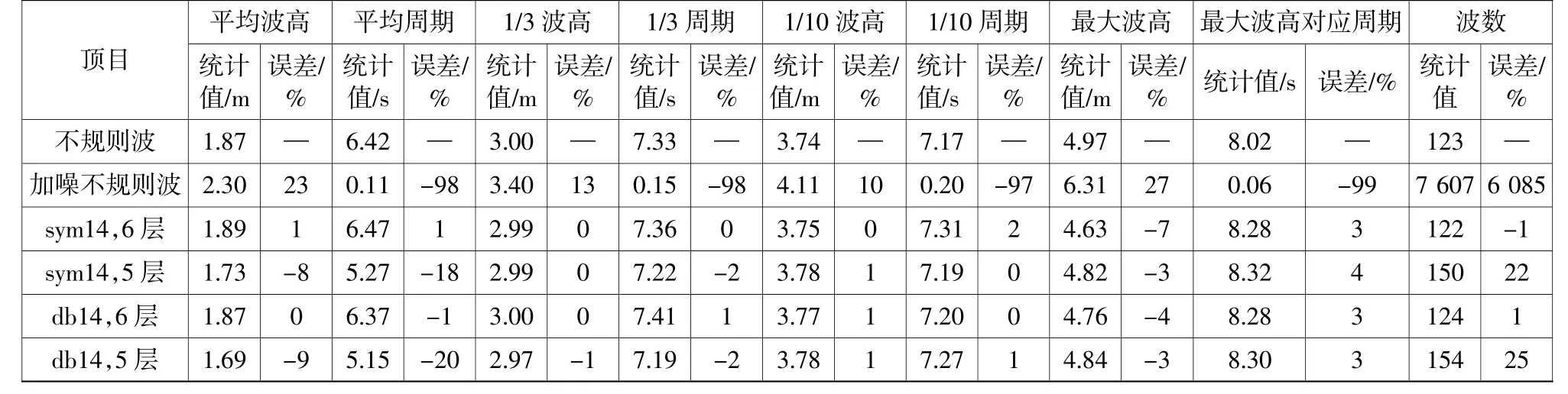
表1 db14和sym14小波函数族对不规则波降噪结果Table 1 De-nosing results of db14 and sym14 wavelet function sets on irregular wave

图2 不同小波对不规则波降噪对比图Fig.2 Comparison of de-noising effectsfor irregular wave applied in different wavelet functions

4 工程应用

图3（a）为某滨海电厂泵房前池的测试波动信号。很明显泵房前池存在长周期波，且有明显“骑波”现象；在静水试验中发现，测试信号噪声主要为高频信号与高斯白噪声。因此根据噪声特征，选取小波函数db14，并进行6层小波分解降噪，其波动过程的时域图见图3（b）。

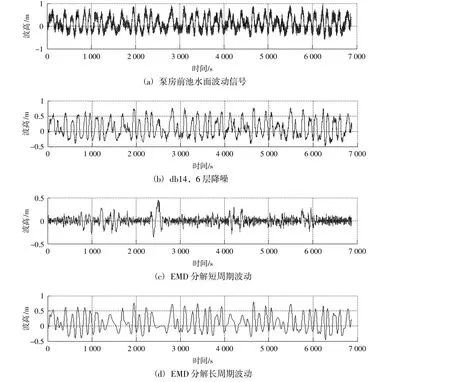
图3 泵房前池波动信号进行小波降噪及利用EMD对降噪后信号进行长短周期分离Fig.3 Applying wavelet function to de-nosing the signal of water level fluctuation in forebay of pump station and use of EMD to separate the long and short period of the single after the noise reduction

降噪统计结果显示，泵房前池的水面波动以长周期波动为主，周期最大达到200 s。通过对降噪后的信号进行EMD分解，得到频率由大到小的15个EMD分量，现以30 s作为长短周期划分的标准，根据图1所述流程对该波动信号进行长短周期分离。

降噪后波动信号及EMD分解长短周期波浪特征统计见表2，降噪后的波动信号有效波高为0.87 m，显然其波高不满足泵房前池的波动要求，但其对应的有效周期为128 s，属于长周期波。在经过EMD分解之后，其短周期波动的有效波高小于0.2 m，周期为16 s；长周期波动的有效波高为1.03 m，周期为147 s。从分解后的结果来看，短周期的波动满足泵房前池的波动要求，但其长周期的水面波动较大，达到1 m，因此，从厂址的安全角度考虑，厂址的厂坪标高应注意长周期波动的影响。

表2 小波降噪及EMD分解后波动信号的统计特征Table2 Parameter statistics of original signal and the de-nosing signal applied in wavelet function and EMD

5 结语

本文通过构造叠加白噪声不规则波，应用小波分析对信号进行降噪处理，结果显示合理地选择小波函数、阈值及分解层数可以对信号进行高精度的降噪；通过对泵房前池波动信号降噪后发现，泵房前池的波动以长周期波为主，利用EMD方法将泵房前池的波动分解为长周期波动及短周期波动，结果显示，短周期波动波高较小，满足泵房前池的取水要求，但长周期波高较大，在考虑泵房前池的取水安全同时，应评估其长周期波动对厂坪标高的影响。

[1] 杨宪章，张文忠，李慧仙，等.岭澳核电站取水头部及取水明渠中的长周期水面波动[J].港口工程，1998（5）：3-10.YANG Xian-zhang,ZHANG Wen-zhong,LI Hui-xian,et al.Long-period fluctuations at the head of inlet and open channel in Ling′ao nuclear power station[J].Harbour Engineering,1998(5):3-10.

[2]史力生，潘军宁.滨海核电站取水渠长周期波动现象及其消减[J].水利学报，2009（2）：201-207，213.SHILi-sheng,PAN Jun-ning.Longperiod wave occurred to coolingwater intake channel of nuclear power stations[J].Journal of Hydraulic Engineering,2009(2):201-207,213.

[3]NB/T 25002—2011，核电厂海工构筑物设计规范[S].NB/T 25002—2011,Code for design of maritime structures of nuclear power plants[S].

[4] 侯树强，王彦龙，刘诗华.滨海核电厂取水泵房前池水位波动控制标准的探讨[J].中国港湾建设，2014（11）：4-7.HOU Shu-qiang,WANG Yan-long,LIU Shi-hua.Control standards for water-level fluctuation on pump-station′s distributing pool of coastal nuclear power station[J].China Harbour Engineering,2014(11):4-7.

[5]HUANGN E,SHENZ,LONGSR.The empirical modedecomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[C]//Proceedingsthe royal society of long SERIESA,1998,454:903-995.

[6] 曹冲锋.基于EMD的机械振动分析与诊断方法研究[D].杭州：浙江大学，2009.CAO Chong-feng.Study on mechanical vibration analysis and diagnosis methods based on empirical mode decomosition[D].Hangzhou:Zhejiang University,2009.