多用途江海直达船模态分析与动力响应预报

,

(上海交通大学 a.船舶海洋与建筑工程学院；b.水动力学教育部重点实验室，上海 200240)

船体振动可分为自由振动和强迫振动两大类，前者主要研究船体总振动的固有频率和固有振型，而后者主要研究船体在不同激励力下的响应。在船舶设计阶段确定船舶尺度、装卸载和推进方案时，需考虑避开主船体的低阶共振。如何获得船体梁自由振动特性，对于采取合理的设计方案和减振措施，避免船体梁与主要激励源发生共振是至关重要的[1]。随着有限元技术的发展，船舶振动计算已经由一维梁模型、二维平面模型发展为整船三维模型。目前已有不少基于数值分析对散货船、集装箱船及油船的振动研究，比如，有限元方法研究、振动耦合研究、计算程序研究和计算与试验对比研究等，标志着我国在船舶振动领域已取得重大科研成果。但是，我国在减小江海直达船振动方面还缺少行之有效的措施，在船舶设计阶段很少考虑振动问题和进行必要的振动计算[2]。

多用途江海直达船因其江海两用的特性，有着中转周期短、货物损耗少、营运成本低等优势，受到国家航运部门和企业的重视。该类船舶在航行过程中，吃水变化大，易受到浅水效应的影响。而且该类船舶目前越来越趋于大型化，又采用多机多桨船型，主机功率和螺旋桨转速也越来越大，使得船舶振动问题越来越突出，并且与主机振动、螺旋桨空泡、船尾部型线等都有密不可分的关系。考虑以典型的2 000 t级江海直达船为例，研究其振动特性。

1 模态分析理论基础及有限元建模

1.1 模态分析理论概述

通过求解振动特征方程，可以得到特征值和特征向量，其分别对应结构的固有频率和模态振型，再根据初始条件求得所需响应，即为模态分析。相比单自由度系统，对多自由度系统进行模态分析时，需要考虑单自由度系统所没有的特性，增加了复杂性，而实际的工程结构均可视为多自由度系统。

系统的运动方程为

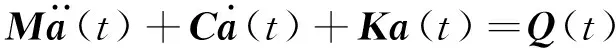
(1)

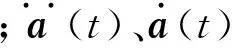
由于在船舶总体振动中，船舶一般假定为一根悬在水面的变截面空心弹性基础梁，为一个平衡力系，整体模型处于弱约束状态，可看成在水面上的无阻尼自由振动，因此，本文以不考虑阻尼影响的系统自由振动为例，解耦方程。

不考虑阻尼时，多自由度系统自由振动方程为

(2)

其方程解为

a=φsin[ω(t-t0)]

(3)

式中：φ为n阶向量即模态振型；ω为φ的振动频率即固有频率；t为时间；t0是初始条件。将式(3)代入式(2)，就得到一个广义特征值问题：

Kφ-ω2Mφ=0

(4)

0≤ω1<ω2<…<ωn

(5)

(6)

(7)

由式(6)和式(7)可以知道固有振型φ对M是正则正交性质，即

(8)

将(8)代入(4)，可得

(9)

定义固有振型矩阵和固有频率矩阵为

Φ=[φ1φ2…φn]

(10)

(11)

求解固有振型矩阵和固有频率矩阵的方法有Lanczos法、Subspace法、Ritz法等。在Abaqus中集成了Lanczos法和Subspace法，可以选择其中之一进行计算。

1.2 有限元建模

以典型的江海直达散货船为例，全船主要为横骨架式结构，少数部分如上甲板、双层底及舷侧，采用纵骨架式结构，船型采用单甲板、双层底、双机、双舵、双桨、尾机船型，全船拥有一个货舱，货舱区域设双壳结构，横剖线图如图1所示。总长85.6 m、垂线间长80 m、型宽14.6 m、型深5.6 m，设计吃水3.8 m总吨位2 000 t。全船为Q235钢，弹性模量E=210 GPa，泊松比v=0.3，屈服强度σ=308 MPa。在建立三维有限元模型时，对上层建筑结构进行简化。船底、甲板和舷侧采用S4R四节点壳单元，骨材采用B31梁单元，建立的整船模型如图2所示，模型采用自由边界条件。

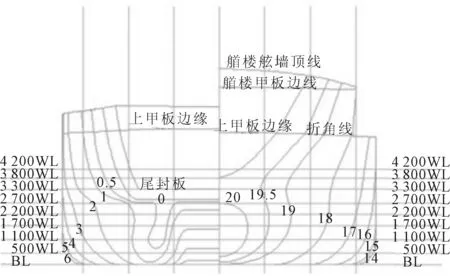
图1 总吨位2 000江海直达船横剖线图

图2 整船有限元模型

2 计算结果及分析

2.1 附连水质量

江海直达船可以由江直接驶入海里，反之亦然。当船舶在浅水中航行时，由于水深受到限制，将会产生浅水效应。此时船体与水的相对速度较深水情况就会有所增大，其增加的速度称为回流速度。由于回流速度的存在，船底流速将会增大，从而船底压力降低，船体下沉，造成吃水增加，而且螺旋桨的推进效率也会随之降低[3]。

当船舶在内河航行时，单位长度上垂向附连水质量公式为

(12)

式中：ρ为水的密度；b为剖面水线半宽；CV为修正系数；d为剖面处船舶吃水；S为水面处船舶剖面面积；Ki为修正系数，主要基于三维流动而定义的，与船的长宽比L/B及船舶振动有关；αv为浅水修正系数，和水深及剖面水线半宽有关。

考虑到浅水效应，采用文献[4]推荐的船舶在浅水航行时船体下沉量计算式

T=2×Cb×V2/100

(13)

式中：T为船舶下沉量，m；Cb为船舶方形系数；V为船速，kN。

计算得到，本船浅水效应下沉量为0.99 m。

当船舶在海水航行时，单位长度上垂向附连水质量为[5]

(14)

参数意义与(12)相同。

得到附连水质量后，连同货物载荷以虚拟质量点的方式平均加到船体上。

2.2 模态分析

选取满载出港和压载到港两种工况，分别取前三阶模态进行分析[6]。两工况部分计算结果见图3、4，具体固有频率见表1。

图3 内河航行满载出港垂向1～3阶模态

图4 海中航行满载出港垂向1～3阶模态

表1 垂向固有频率汇总 Hz

由结果可以看出，相比于海中航行工况，在内河航行时，船体固有频率略低，主要是因为受到浅水效应的影响，吃水加深，附连水质量加大。由内河浅水区向深水区行驶时，是易发生船体共振阶段，因为由于吃水的变化导致主机和螺旋桨转速发生变化，因而主机和螺旋桨激励频率也将跟着发生变化，在选择主机和螺旋桨转速时应注意避开船体共振。

2.3 动力响应计算

2.3.1 主机激励和螺旋桨激励

为了更好地了解江海直达船的振动特性，除了振型之外还需要进行一些必要的动力响应预报。主机和螺旋桨是船舶振动的主要振源之一，本船型所使用的主机和螺旋桨参数见表2、3。

表2 船舶主机参数

表3 船舶螺旋桨参数

主机激励主要是指主机工作时对船体产生的周期性力、周期性力矩。而螺旋桨工作时所引起的激振力相比于主机激励要更加复杂，大致分为两类：表面力和轴承力[7]。其中，表面力是主要振源，若螺旋桨产生空泡，桨表面力要增大几十倍。本文用DNV规定的方法，估算该船的脉动压力峰值[8]。见式(15)、(16)。

(15)

式中：Δp0为不计空泡影响的脉动压力峰值,Pa；n为螺旋桨转速，r/min；Dp为螺旋桨直径,m；z为桨叶数；ds为叶片位于正上方时，0.9R螺旋桨半径处距船体距离，m；R为螺旋桨半径，m；K0为系数，当ds/R≤2时，K0=1.8+0.4ds/R；当ds/R>2时，K0=2.8。

(16)

式中：Δpc为计及空泡影响的脉动压力峰值，Pa；Vs为船速，m/s；ha为桨轴沉深，m；Kc为系数，当ds/R<1时，Kc=1.7-0.7ds/R；当ds/R≥1时，Kc=1.0；wamax为伴流分数的最大值；we为伴流分数有效值。

总脉动压力峰值为

(17)

螺旋桨激振力为

(18)

式中：np为主机额定功率时螺旋桨转速；n为低于np的其他转速；Fmax为主机额定功率时螺旋桨的激振力；F为螺旋桨转速为n时的螺旋桨激振力。

螺旋桨表面力属于叶频干扰力，其频率为

f=n×z/60 Hz

(19)

本船在主机额定转速下运行时，其主机激励频率为12.5 Hz，螺旋桨叶频激励为16.7 Hz，倍叶频激励为33.4 Hz。根据CCS要求，为了防止共振的发生，船舶固有频率需要满足一定的频率储备，也就是各激振力频率需要避开的频率[9]，见表4。

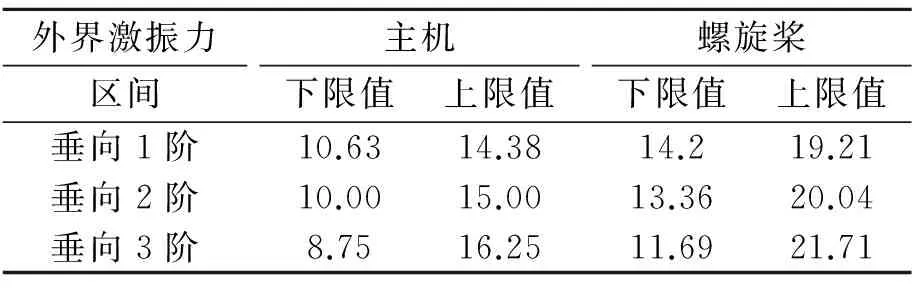
表4 船舶固有频率频率储备 Hz

由计算结果可知，船舶在主机额定转速下运行时，船体梁的固有频率都远低于船舶固有频率储备的下限值，说明该船设计良好，不会发生强烈共振。但是当船舶在由内河转入海里航行时，主机和螺旋桨激振力频率将发生变化，需要注意合理地调整主机和螺旋桨转速，使主机和螺旋桨激振力频率与船舶固有频率错开，并满足频率储备的要求。同时，所计算的船舶固有频率，可以为选择主机及螺旋桨转速提供参考，避免共振现象发生。

2.3.2 加速度响应幅值

根据上节的介绍，可以得出主机和螺旋桨激励力，然后选取船舶典型节点作为研究对象，计算其加速度响应。取机舱上主甲板左舷处(节点编号911)、货舱左舷处(节点编号3673)和首压载水舱主甲板中线处(节点编号10227)为研究对象。考虑了主机和单浆共同激励以及主机和双桨共同激励的情况，由Nastran计算结果见图5、6。

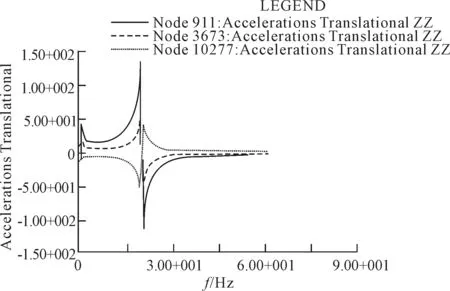
图5 主机和单浆共同激励下节点加速度响应幅值

图6 主机和双浆共同激励下节点加速度响应幅值

结果显示，主机额定转速下，单浆工作状态船舶振动加速度响应要大于双桨工作时，说明船舶双桨工作振动性能好于单桨工作。而且靠近船艉区域振动最大，艏部次之，中部区域振动最小；沿吃水方向，振动响应随着距船体底部的距离的增大而减小。

3 结论

1)浅水效应导致船舶下沉，使船舶吃水加深，附连水质量加大。满载出港时，船舶固有频率降低10%～15%；压载到港时，船舶固有频率降低12%～30%。这是因为满载比空载船舶总体质量大，振动频率低，不易发生大的振动。

2)船舶由内河浅水区驶入深水区或者海中时，是共振易发阶段，主要是因为单双桨交换工作，主机和螺旋桨激励频率变化大，期间很可能没有错开船体某阶固有频率。而且单桨工作时，相比于双桨工作船舶振动幅度增大了40%，因此船舶航行时宜采用双桨同时推进的方式航行。

3)除艉部区域振动外，艏部振动也比较大，主要因为艏部压载增加吃水，加重了船舶的振动，建议减少艏部压载重量，或采取其他方式调整平衡。

在后续的船舶设计与建造中，应充分考虑引起振动的不利因素，避开共振频率，如考虑压载水、油等液体在舱内的晃荡，风、浪、流载荷对船舶振动的影响，以及浅水效应时船底流体旋涡及粘

性对螺旋桨激励等的影响。此外，为更准确地评估全船振动时，还应分析水平振动和扭转振动。

[1] 周清华,肖蕾,耿厚才.VB.NET和NASTRAN混合编程在船体梁振动计算中的应用[J].船海工程,2017,46(2):69- 72.

[2] 骆庆卫.内河船舶振动及减振措施[J].江苏船舶,2004:21(5):17- 18.

[3] 周清华,李祥宁,胡要.滑行艇尾部结构的模态分析和响应预报[J].舰船科学技术，2011(7):50- 53.

[4] J.N. Newman. The Theory of Ship Motions[J]. Advances in Applied Mechanics,1979(18):221- 283.

[5] 姚熊亮.船体振动[M].哈尔滨：哈尔滨工程大学出版社,2004.

[6] 赵振轶.小水线面双体船总振动分析计算[D].大连：大连理工大学,2016.

[7] 王智群.某94.8 m集装箱船的振动分析与噪声预报[D].广州：华南理工大学,2016.

[8] A. Jha, E. Nikolaidis, S. Gangadharan. Cyclostationary Random Vibration of a Ship Propeller[J]. Journal of ship research,2003,47(4):299- 312.

[9] 中国船级社. 船上振动控制指南2000[S].北京：人民交通出版社,2000.