基于相干分析的汽车轮心力对振动噪声贡献的对比研究

王 策，丁 康，杨志坚

（华南理工大学机械与汽车工程学院，广州 510641）

前言

路面激励是汽车最重要的激励源，它引起车辆的振动和噪声，对整车的NVH(噪声、振动和声振粗糙度)性能有很大影响。由路面作用在行驶车辆的轮心力包括沿3个方向的力和绕3个方向的力矩，采用合理有效的方法计算轮心六自由度激励对车辆目标点振动噪声的贡献率、对车辆NVH性能分析具有重要的指导意义。贡献率计算方法主要有传递路径分析和相干分析两种。目前针对传递路径分析的研究已较成熟[1－5]，而针对相干分析的却较少。国内外对相干技术的应用主要局限于常相干法、偏相干法和多重相干法[6]。常相干法只适用于非相关激励；偏相干法可适用于相干激励，但其对信号源优先级存在依赖性，不同的优先级排序会产生不同的计算结果，因此对物理解释的影响较大，且计算比较复杂[6－7]；多重相干法通过将相关性强的各个激励分为一组，组与组之间的相关性忽略不计，而计算出各组激励对目标点响应的贡献率。文献[8]中采用多重相干法分解汽车路面噪声，通过实验得出轿车的4个车轮是路面噪声的4个独立源的结论，进而分析了4个车轮各自对路面噪声的贡献率。虚相干法也是相干技术的一种，它可考虑激励中存在相关性的情况，同时具有明确的物理意义[9－10]。

本文中首先阐明了多重相干法与虚相干法的基本理论，针对路面激励贡献率计算的问题，分析了两种方法的优势与不足。通过实验识别六自由度轮心力，分别采用多重相干法和虚相干法处理实验数据，结果表明，在计算路面激励贡献率时，多重相干法存在明显的不足，而虚相干法能够取得较好的结果。

1 轮心力贡献率计算方法

要计算轮心力对目标点响应的贡献率，首先要识别轮心力并检验识别效果，过程如下。

(1)采用文献[11]和文献[12]中所述的方法识别六自由度轮心力。在每个车轮轮缘布置3个或以上的激励点，在每个车轮附近布置2个或以上的三向加速度传感器(响应点)，使用力锤沿3个方向敲击每个激励点，得到轮缘到响应点的传递函数，利用这些传递函数和激励点相对于轮心的坐标，计算六自由度轮心力到响应点的轮心传递函数。路试时采集各响应点信号，通过直接求逆法计算六自由度轮心力。

(2)验证激励识别的准确性。利用轮心力和轮心力到目标点的传递函数计算目标点的识别响应，与目标点的实测响应对比，在二者一致性较好的频段，激励识别是准确的。

在准确识别轮心力的基础上，分别采用多重相干法和虚相干法处理实验数据，分析实验结果。

1.1 多重相干法

对于一个多输入单输出的线性时不变系统，在平稳随机激励作用下，响应的自谱密度和激励与响应间的互谱密度分别[13]为

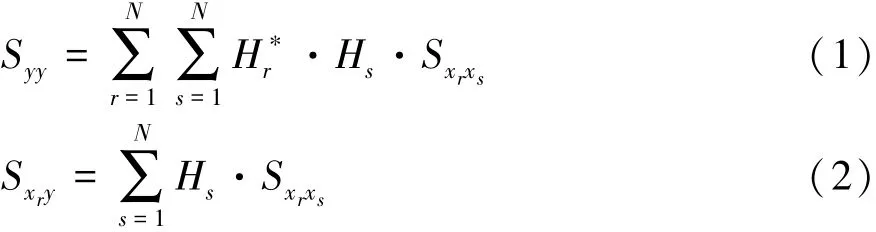
式中:N为激励的自由度数；Hr和Hs分别为激励xr和xs到响应y的传递函数；Sxrxs为激励xr与xs的互谱密度；Sxry为激励xr与响应y的互谱密度。

激励xr与响应y的常相干系数为

式中Sxrxr为激励xr的自谱密度。

当激励间不存在相关成分时，任意两个不同激励间的互谱恒为零。此时，式(1)和式(3)可以简化为

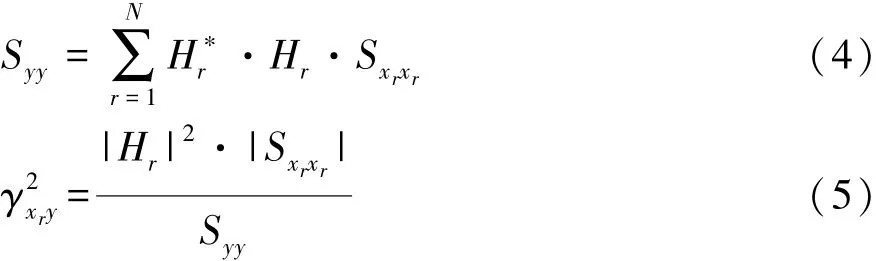
由式(4)和式(5)可以看出，当激励间不存在相关成分时，常相干系数反映了不同频率下激励xr在响应y中的能量贡献率。

而当激励间存在相关成分时，激励间的互谱不恒为零，根据式(1)和式(3)，并不能反映出不同频率下激励xr在响应y中的能量贡献率。

假设x1，x2，…，xM(M≤N)为一组彼此相关的激励，记为E，则E与响应y的多重相干系数定义为

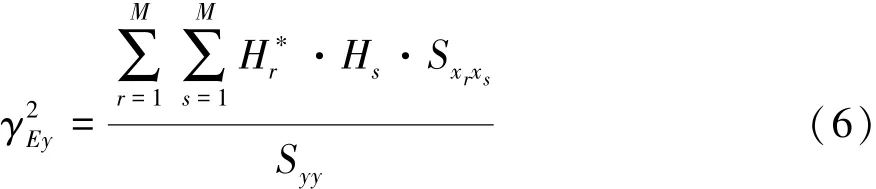
当E中各激励与除E之外的其余激励两两之间的所有常相干系数都很小时，即可视为E对响应y的能量贡献率。

由此可见，采用多重相干法计算相关性激励的能量贡献率问题，其实质是对常相干系数法的推广，因此存在以下两个问题:

(1)只有在能够将所有激励划分成彼此之间相关性小的分组时，使用多重相干法才有意义；

(2)只能够计算分组整体对响应的能量贡献率，而无法计算分组内单个激励自由度的贡献率。

1.2 虚相干法

对于多输入单输出系统，响应的自谱密度和响应与激励间的互谱密度的向量为

式中:H为传递函数向量；Sxx为激励功率谱密度矩阵。

由于Sxx为厄米特矩阵，其奇异值可分解为[14]式中:U 为奇异向量矩阵；Sx′x′为奇异值矩阵，也称为虚激励功率谱密度矩阵。

由式(7)和式(9)可得，响应自谱密度为

令虚传函向量为

则式(10)可写为

由式(8)和式(9)得

令虚互谱矩阵为

由式(11)、式(13)和式(14)得

对比式(12)与式(7)、式(15)与式(8)，不难看出它们之间存在着相似性。由于Sx′x′为对角矩阵，也即虚激励间不存在相关性，则可通过计算虚激励与响应的常相干系数，此时称为虚相干系数，来表示第i′个虚激励xi′对响应y的能量贡献率:

式中:Syi′为 Syx′中的第 i′个元素；Si′i′为 Sx′x′的对角线上第 i′个元素。

由式(9)中可以看出，由于 Sx′x′为对角矩阵，故可通过计算虚激励与实际激励的虚相干系数表示xi′在第i个实际激励xi中的能量贡献率:

式中:Sii为 Sxx对角线上第 i个元素；Sii′为 Sxx·U 的第i行、第i′列所在元素。

虚激励的能量分配到各个实际激励中，有

则xi在xi′中的能量贡献率为

由式(16)和式(19)可以计算出xi对响应y的能量贡献率为

则所有实际激励i对响应y的能量贡献率之和为

理论上，式(21)的值为1，但由于外界干扰和系统非线性等因素的影响，其实际值小于1。

由此可见，采用虚相干法能直接计算相关性激励中单个激励自由度对响应的能量贡献率，从而避免了多重相干法存在的问题。

针对汽车路面激励贡献率计算的问题，由于汽车直线行驶时前轮与后轮经过的路面只有一个时间差，而左右轮悬架对称且路面平整度基本相同，因此作用在不同车轮上的各自由度激励力间存在着较大的相关性。采用多重相干法时，如果将单个车轮上受到的所有激励分为一组[5]，不仅无法分析单个轮心力的贡献率，如果不同分组间的相关性较大，甚至无法计算激励分组的贡献率。而采用虚相干法却能够直接计算六自由度轮心力的贡献率，无论激励是否相关。由于轮心力是通过识别得到而非直接采集，只能通过式(8)计算激励与识别响应的互谱密度矩阵，所以采用虚相干法只能计算轮心力对识别响应的贡献率，而无法计算对实际响应的贡献率，此时式(21)的值恒为1。

2 路面激励识别实验

2.1 实验步骤

实验车为一辆四轮电动沙滩车。实验分传递函数测试和路试两部分进行。实验场景及各加速度传感器测点布置如图1所示。以车辆前进方向为＋X方向，以前进方向的左侧为＋Y方向，以竖直向上为＋Z方向。在与每个车轮临近的非随车轮旋转的位置(如转向节)布置3个三向加速度传感器，其中左前轮的1个传感器将用于检验激励识别的准确性，称为目标点，其余传感器均用于轮心激励力识别。

图1 实验图和测点图

传递函数测试时，为使悬架状态与路试时一致，在驾驶员位置放置与路试员质量相近的重物，用弹性绳绕过每个悬架靠近车轮的位置将整车吊起，使与所有车轮底部相切的平面保持水平。由于无法做到重物的位置与路试时完全一致，因此整车的质心与路试时有一定区别，但这对系统的弹性体模态影响很小。由于轮辐为内凹曲面，不易布置激励点，故拆下车轮，在每个车轮轮毂安装圆盘，并选择4个激励点，记录其相对于轮心的坐标。使用力锤沿3个方向敲击各激励点，测得所有的传递函数。其中，1号激励点(位于左前轮轮毂安装盘)－Z方向到1号响应点(位于左前轮转向节)＋Y方向的传递函数幅频特性与对应的相干函数如图2所示。

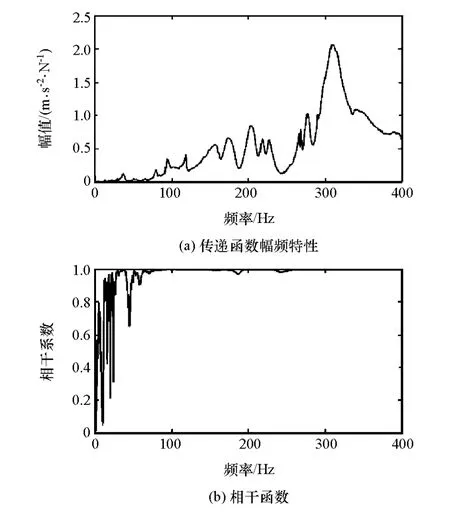
图2 1号激励点－Z方向到1号响应点＋Y方向的传递函数幅频特性及相干函数图

路试选择在平整的高级路面进行，驾驶员位置坐人，车速达到10km/h后保持恒定开始采集各传感器时域信号，85s后停止采集。重复3次。其中，1号响应点＋Z方向加速度时域信号如图3所示。

2.2 识别结果

利用左前轮的两个加速度传感器和其余每个车轮的3个加速度传感器的响应信号识别六自由度轮心力，然后计算左前轮目标点响应。目标点的实测响应与识别响应如图4所示。

(1)识别响应与实测响应在0～400Hz整个频率范围趋势一致。

图3 1号响应点＋Z方向加速度时域信号

(2)在100～400Hz，识别响应比实测响应小，二者绝对误差在0.001m2/s4以下。

(3)在0～100Hz，＋X方向在各个频率处均存在一定相对识别误差；＋Y方向相对识别误差在峰值频率处较大，其余频率处较小；＋Z方向相对识别误差最小，这是因为汽车在平直路面行驶时轮胎主要受到＋Z方向的激励，使左前轮目标点＋Z方向的响应比另外两个方向更大。

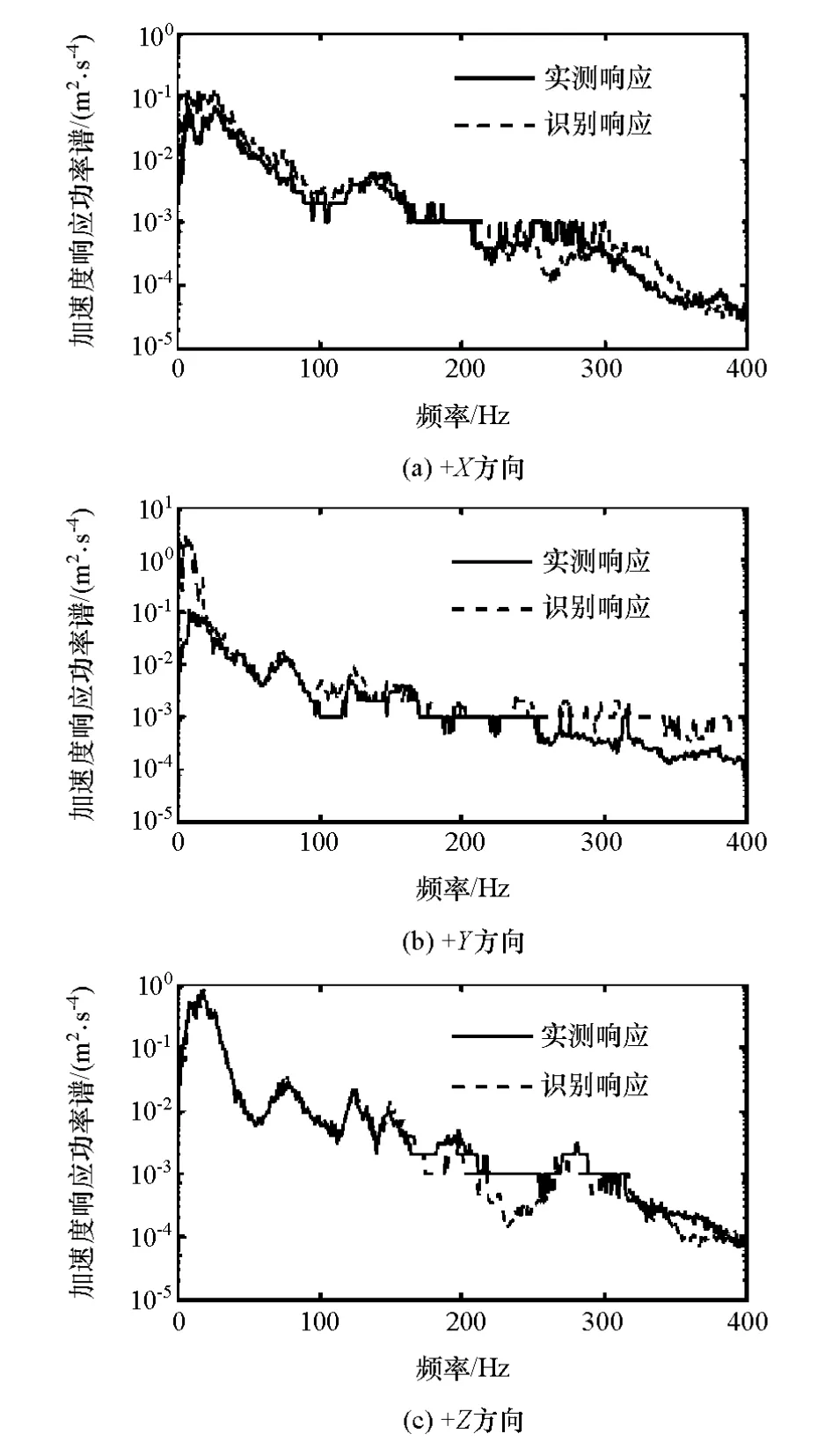
图4 目标点实测加速度响应自谱密度与识别响应自谱密度对比图

(4)＋Z方向的实测响应峰值是另外两个方向实测响应峰值的10倍，峰值频率17Hz对应于悬下质量的偏频。

综上所述，由于目标点＋Z方向的识别误差较小且响应峰值最大，下面将以＋Z方向响应为例，分别采用多重相干法和虚相干法分析激励分组或单个激励在各个频率下尤其是峰值频率17Hz处的能量贡献率。

2.3 贡献率

(1)多重相干法 参考文献[5]中的思路，将单个车轮上受到的所有激励分为一组，计算各组激励的贡献率。首先，计算不同车轮的各自由度激励力间的常相干系数，其中左前轮＋Z方向与左后轮＋Z方向的激励力之间的常相干系数如图5所示，它在多个频段范围内都大于0.1，此时不同激励分组间的相关性不能忽略。因此采用多重相干法计算激励分组的贡献率将引入较大的误差，其结果如图6和表1所示。由图6可见，各轮激励能量贡献率之和在10～50Hz处远大于1，这与该频段内识别响应与实测响应误差较小的结果不符，这是由于不同车轮的各自由度激励力间相关性较大造成的。表1所示的结果同样说明了这一点。

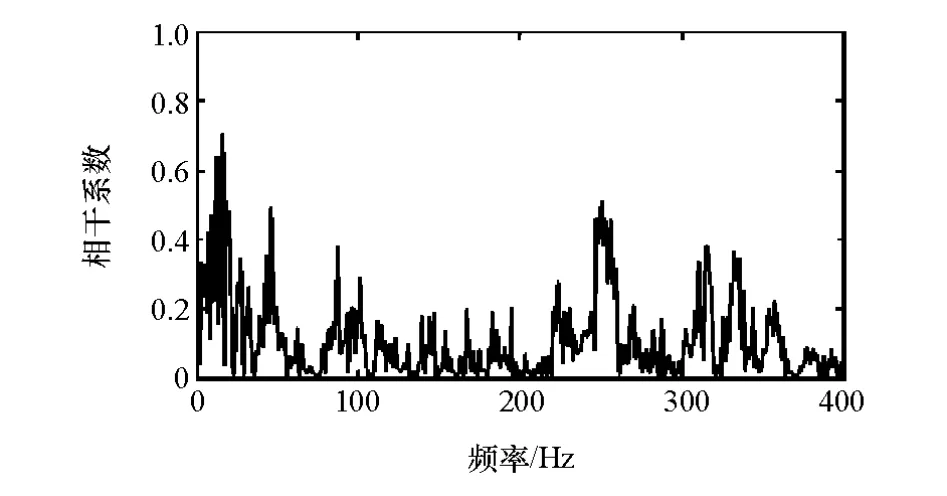
图5 左前轮＋Z方向与左后轮＋Z方向的激励力之间的常相干系数

图6 多重相干法得到的各轮激励能量贡献率之和

表1 峰值频率17Hz处各车轮激励组能量贡献率(多重相干法)

(2)虚相干法 采用虚相干法计算各激励自由度的能量贡献率，分别对所有力和力矩的贡献率求和，如图7所示。由图7可见，在0～400Hz力贡献率之和接近于1，力矩贡献率之和很小，接近于0。将单个车轮上的所有轮心力贡献率相加，得到各个车轮激励贡献率，如图8所示。

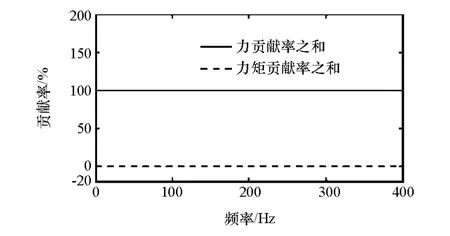
图7 虚相干法得到的力贡献率之和与力矩贡献率之和

峰值频率17Hz处各激励自由度能量贡献率如表2所示，由于力矩的贡献与力相比很小，所以不再考虑。由表2可以看出，由于目标点靠近左前轮，所以左前轮心激励对目标点的贡献最大，其次是右前轮和左后轮，右后轮的贡献相对较小。对比表1和表2中的两种方法得到的轮贡献率结果，发现两者有很大差别，这是由于不同车轮激励间存在较强的相关性，采用多重相干法计算的结果是错误的，而虚相干法能很好地适应这一点。

表2 峰值频率17Hz处激励能量贡献率(虚相干法，不考虑力矩)

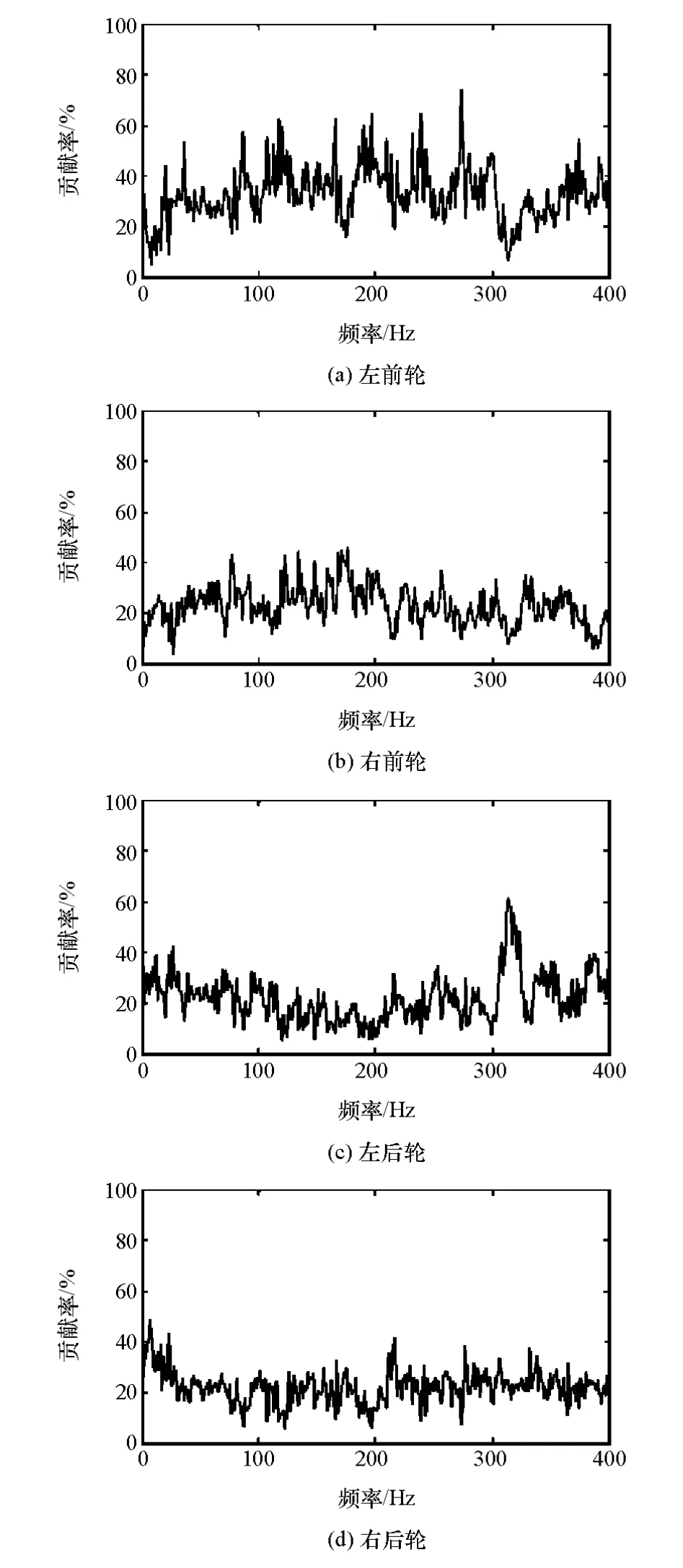
图8 虚相干法得到的各轮激励能量贡献率

3 结论

针对汽车路面激励贡献率计算的问题，由于不同车轮受到的路面激励之间和单个车轮受到的不同自由度激励之间均存在一定的相关性，故难以直接应用常相干法求解，分别通过理论分析和实验计算对比了多重相干法和虚相干法，得出以下结论。

(1)通过理论分析指出，采用多重相干法计算相干激励的贡献率时存在的两个问题:只有在能将所有激励划分成彼此之间相关性很小的分组时，使用多重相干法才有意义；只能计算分组整体对响应的能量贡献率，而无法计算分组内单个激励自由度的贡献率。实验结果表明在激励分组(单个车轮上的所有激励为一组)之间存在较大的相干性时，采用多重相干法计算得到的贡献率误差较大。

(2)阐明了虚相干法的基本理论，无论激励是否相关，采用虚相干法均能直接计算轮心六自由度激励的贡献率。但与多重相干法相比，虚相干法的理论较为复杂。

[1] 郭荣，万钢，左曙光.燃料电池轿车车内噪声传递路径分析研究[J].汽车工程，2007，29(8):635－641.

[2] 龙岩，史文库，梁天也，等.基于改进传递路径分析法的动力总成悬置系统优化及评价[J].汽车工程，2009，31(10):957－962，985.

[3] 余雄鹰，闵福江，文伟，等.轮胎/路面噪声的结构传递路径分析[J].汽车工程，2013，35(11):1030－1034.

[4] 王万英，靳晓雄，彭为，等.轮胎振动噪声结构传递路径分析[J].振动与冲击，2010，29(6):88－91，95.

[5] 叶刚，周鋐.基于多参考传递路径分析的路面噪声研究[J].汽车技术，2014(1):29－33.

[6] 陈茉莉，李舜酩.信号源识别的相干函数法[J].中国机械工程，2007，18(1):95－100.

[7] 宋晶.利用偏向干函数法识别汽车整车噪声源的研究[D].成都:西华大学，2006.

[8] 杨洋，褚志刚.汽车路面噪声多重相干分解方法研究[J].振动与冲击，2015，34(19):31－36.

[9] LMS International.Transfer path analysis:the qualification and quantification of vibro-acoustic transfer paths[Z].LMS Application Note，2005.

[10] OTTE D，SAS P，VAN D P P.Principal component analysis for noise source identification[C].International Modal Analysis Conference(IMAC)，1988:1207－1214.

[11] 刘东明，岳亮亮，龚超，等.六自由度轮心力在车内噪声分析中的应用[J].噪声与振动控制，2014，34(1):101－103，108.

[12] GAGLIANO C，MARTIN A，COX J，et al.A hybrid full vehicle model for structure borne road noise prediction[C].SAE Paper 2005－01－2467.

[13] 甘幼琛，谢世浩.随机振动的基本理论与应用[M].长沙:湖南科学技术出版社，1982.

[14] 戴华.矩阵论[M].北京:科学出版社，2002.