基于极限车速的车辆稳定性控制研究

金 辉，李世杰

（北京理工大学机械与车辆学院，北京 100081）

前言

车辆主动安全控制技术一直是底盘技术研究的一个重要领域，而车辆稳定性又是其中的重要一环。目前，国内外的车辆转向稳定性研究，主要以汽车电子稳定程序ESP(electronic stability program)的开发为主，Bosch和BMW等公司都先后开发出了可量产装车的ESP系统，提高了车辆的主动安全性[1]。同时，以ESP结合驱动防滑系统ASR(acceleration slip regulation)和主动悬架系统 ASS(active suspension system)等系统的底盘集成控制也成为研究热点[2－4]。

车辆状态判断是各类稳定性控制系统研究的基础，目前国内外研究主要基于车辆动力学参数来判断车辆行驶状态，如文献[5]中根据轮胎特性分析车辆稳定性，文献[6]中根据车辆横摆角速度响应来分析车辆稳定性，文献[7]中利用横摆角速度-质心侧偏角相平面图进行分析。在实际运用中，目前基本采用线性模型横摆角速度法作为控制系统开关。然而，车辆横摆角速度等信息对于驾驶员来说不具有直观性，且依靠此类判据时对于车辆稳定状态判断不够准确，控制系统无法起到好的控制效果，从而无法保证车辆安全性。

针对以上问题，本文中提出了一种基于极限车速的稳定性控制方法。建立车辆8自由度侧向动力学模型，在已知车辆行驶条件的情况下，通过建立质心侧偏角 质心侧偏角速度相平面图，划分稳定区域，结合车辆自身动力学特性，计算车辆在给定行驶条件时的极限车速。以此车速作为控制开关，设计基于质心侧偏角和横摆角速度的模糊控制器，对模糊控制器输出的补偿横摆力矩，采用前后轮制动力矩比例分配的方法，设计了一套完整的稳定性控制策略。最后对该控制策略进行了仿真和模拟驾驶实验验证。

1 车辆动力学模型的建立

1.1 车辆模型

为真实反映车辆运动情况，本文中建立8自由度侧向动力学模型。考虑了车辆的纵向、侧向、横摆、侧倾运动和4个车轮的滚动。整车受力分析如图1所示。

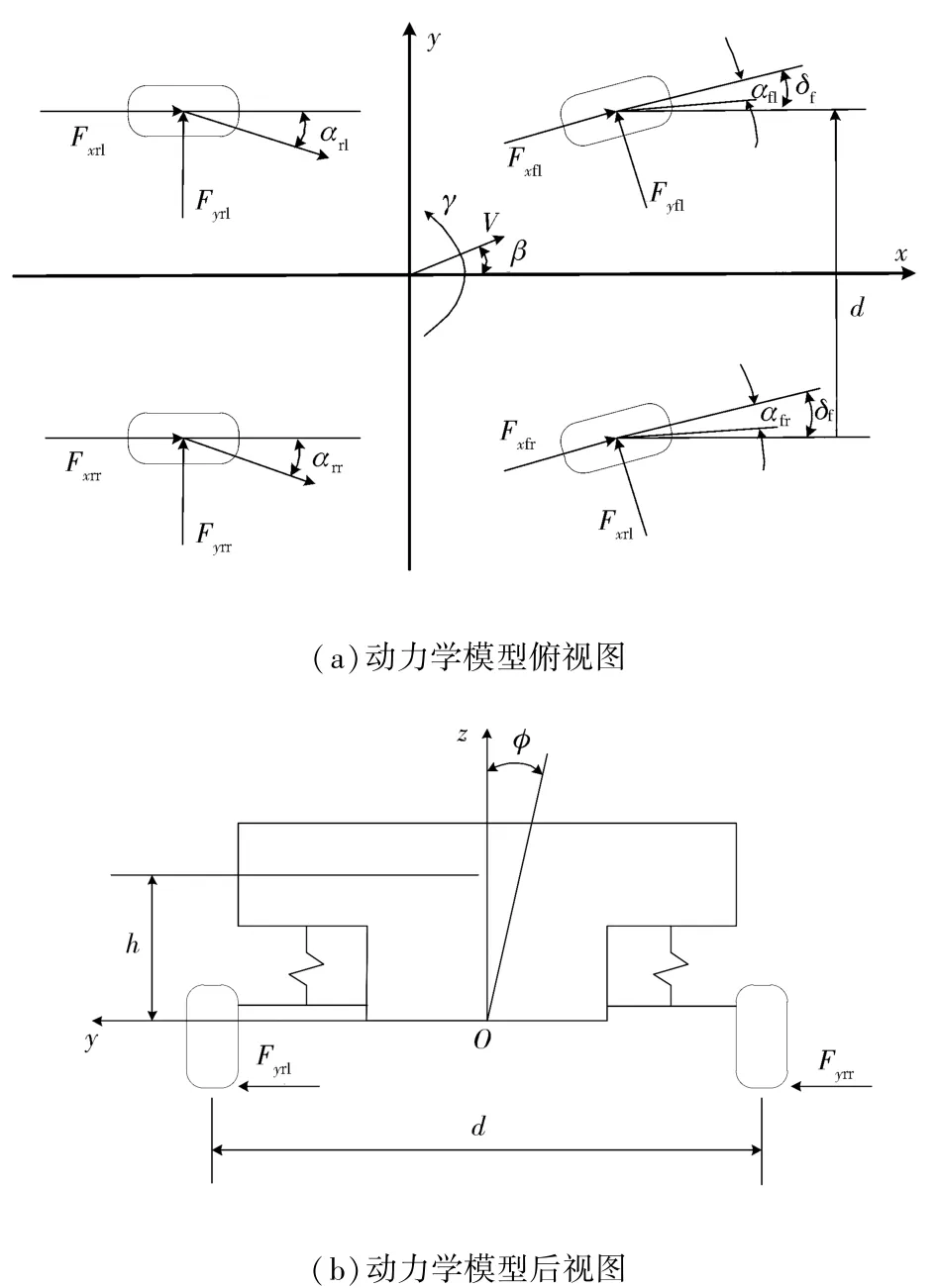
图1 侧向动力学模型

车辆坐标系中，沿x轴的纵向运动方程为

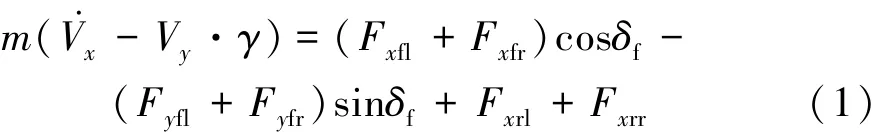
式中:m为整备质量；Vx为纵向速度；Vy为侧向速度；γ为横摆角速度；δf为前轮转角；Fxfl为左前轮纵向力；Fxfr为右前轮纵向力；Fyfl为左前轮侧向力；Fyfr为右前轮侧向力；Fxrl为左后轮纵向力；Fxrr为右后轮纵向力。

沿y轴的侧向运动方程为

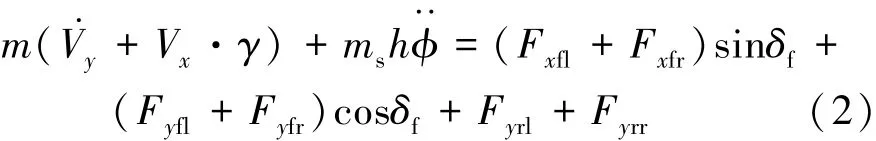
式中:ms为悬挂质量；h为质心高度；Fyrl为左后轮侧向力；Fyrr为右后轮侧向力；φ为侧倾角。

绕z轴的横摆运动方程为

式中:Iz为车辆绕z轴的转动惯量；lf为质心到前轴的距离；lr为质心到后轴的距离；d为轮距；Ixz为悬挂质量对x和z轴惯量积。

绕x轴的侧倾运动方程为

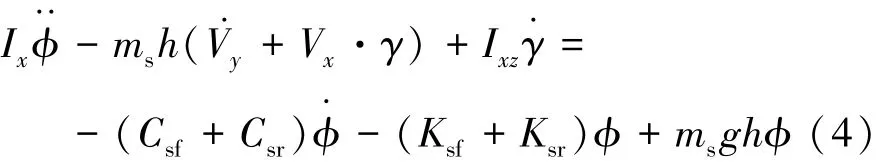
式中:Ix为车辆绕x轴的转动惯量；C为悬架等效阻尼系数；K为悬架等效侧偏刚度。

四轮运动方程为

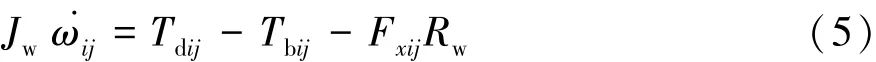
式中:Jw为轮胎转动惯量；ωij为四轮转动角速度；Tdij为4个车轮的驱动力矩；Tbij为4个车轮的制动力矩；i＝ f， r(f代表车辆前轮，r代表车辆后轮)；j＝ l，r(l代表车辆左轮，r代表车辆右轮)；Rw为车轮滚动半径。

1.2 轮胎模型

本文中采用“魔术公式”轮胎模型计算轮胎力，轮胎纵向力计算公式为

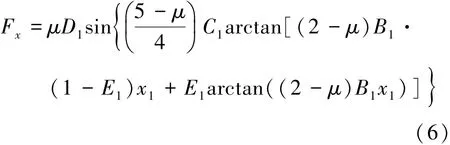
式中:μ为路面附着系数；x1为轮胎滑移率；B1＝B1C1D1/(C1·D1)为刚度因子；C1为形状因子，取值为 1.65；D1＝＋a2Fz为峰值因子；B1C1D1＝(＋ a4Fz)·e－a5Fz为零点处的纵向刚度；E1＝＋aF＋a为曲率因子。

轮胎侧向力计算公式为

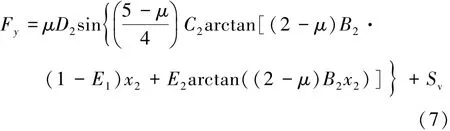
式中:x2为轮胎侧偏角；C2为形状因子，取值为1.3；Sv为垂直偏移量；B2C2D2＝b3[sinb4arctan(b5Fz)]×(1－b11γ)为零点处纵向刚度，其他字母含义与计算纵向力的公式中相同。上式中ai和bi取值见文献[8]。

1.3 制动器模型

制动系统作为车辆系统重要的一部分，在涉及到稳定性控制时，制动系统更会起到非常关键的作用，本文中制动器模型选取盘式制动器，制动力矩M与管路压力p的关系为

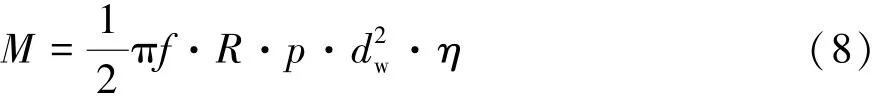
式中:f为摩擦因数；R为制动盘摩擦半径；dw为制动钳活塞直径；η为总泵机械效率。

2 极限稳定车速计算

2.1 质心侧偏角-质心侧偏角速度相平面

车辆系统是一个非常复杂的非线性动力学系统，本文中利用相平面法分析车辆稳定性。对8自由度模型做简化得到非线性2自由度模型:

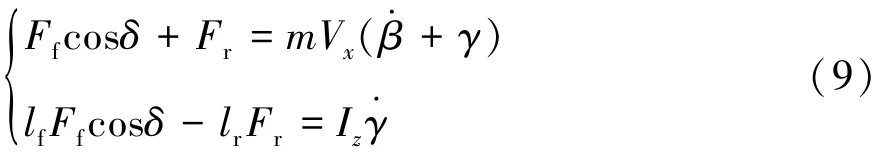
式中:Ff为前轮纵向力；Fr为后轮纵向力。

此时可将车辆系统表示为

此 时 对 于 某 一 初 始 状 态 (β(0)，γ(0))，(β(t)，γ(t))是该方程的解，对于所有 t≥0的时刻，其解就为从(β(0)，γ(0))出发的一条相轨迹，选取不同的初始状态，即可绘制出多条相轨迹，从而构成质心侧偏角-横摆角速度相平面。同时，对于某一初始状态(β(0)，γ(0))，具有对应的初始质心侧偏角-质心侧偏角速度状态(β(0)，(0))，对于所有t≥0的时刻，绘制其相轨迹可以得到质心侧偏角-质心侧偏角速度相平面图。有研究表明，β－相平面相比β－γ相平面更适合车辆稳定性分析[9]，因此本文中利用β－相平面进行车辆稳定极限车速计算。

2.2 相平面稳定区域划分

相平面图是由多条相轨迹组成的，一般来说可将收敛于平衡点的相轨迹构成的区域视作稳定区域，而发散的相轨迹构成的区域视为不稳定区域。对于车辆β－相平面，当车辆行驶车速、前轮转角和行驶路面附着系数有所不同时，β－相平面图稳定区域也会发生变化。不同条件下的β－相平面图如图2所示。

从图2可以看出，当车速较低，路面附着系数较高，无前轮转角时，如图2(a)所示β－相平面图二、四象限相轨迹基本收敛，稳定区域较大。当车速增大时，部分相轨迹在收敛过程中发生振荡如图2(b)所示。当路面附着系数降低为0.2时相平面如图2(c)所示，多数相轨迹不收敛，相平面图稳定区域减小。而当前轮转角增加至3°时，相平面如图2(d)所示，其稳定点向左偏移，相轨迹在收敛过程中出现明显振荡。通过图2可知，相平面图稳定区域与车辆行驶条件有着密不可分的关系，因此在不同行驶条件下，β－相平面图有不同的稳定区域。

取路面附着系数为0.8，前轮转角3°，将车速按10km/h的间隔从30增加到80km/h，得到各个车速下的相平面图和稳定边界，如图3所示。

图3 不同车速下稳定边界

从图3中可看到，随着车速的不断增大，相平面图平衡点不断发生偏移，相平面图稳定区域不断减小，二、三象限的相轨迹在收敛过程中的振幅逐渐增大，且两侧稳定边界倾斜程度不断增大，通过计算分析得到两侧稳定边界方程的斜率和截距，如表1所示。

表1 不同车速下稳定边界

2.3 极限车速计算

对于车辆自身来说，在车速、路面附着系数及前轮转角不同的情况下，其质心侧偏角-质心侧偏角速度轨迹也不同，在稳定区域边界图上画出其质心侧偏角-质心侧偏角速度轨迹曲线，即可看出此曲线在稳定区域内还是超出稳定边界，从而判断车辆的稳定性。通过限定路面附着系数与前轮转角，慢慢增加车速来判断自身轨迹曲线是否超出稳定边界，可最终得到一个车辆自身轨迹刚好处于边界的临界值，进而得到车辆的稳定车速。图4(a)和图4(b)分别为车速为60和80km/h时车辆自身参数曲线与稳定边界的关系。

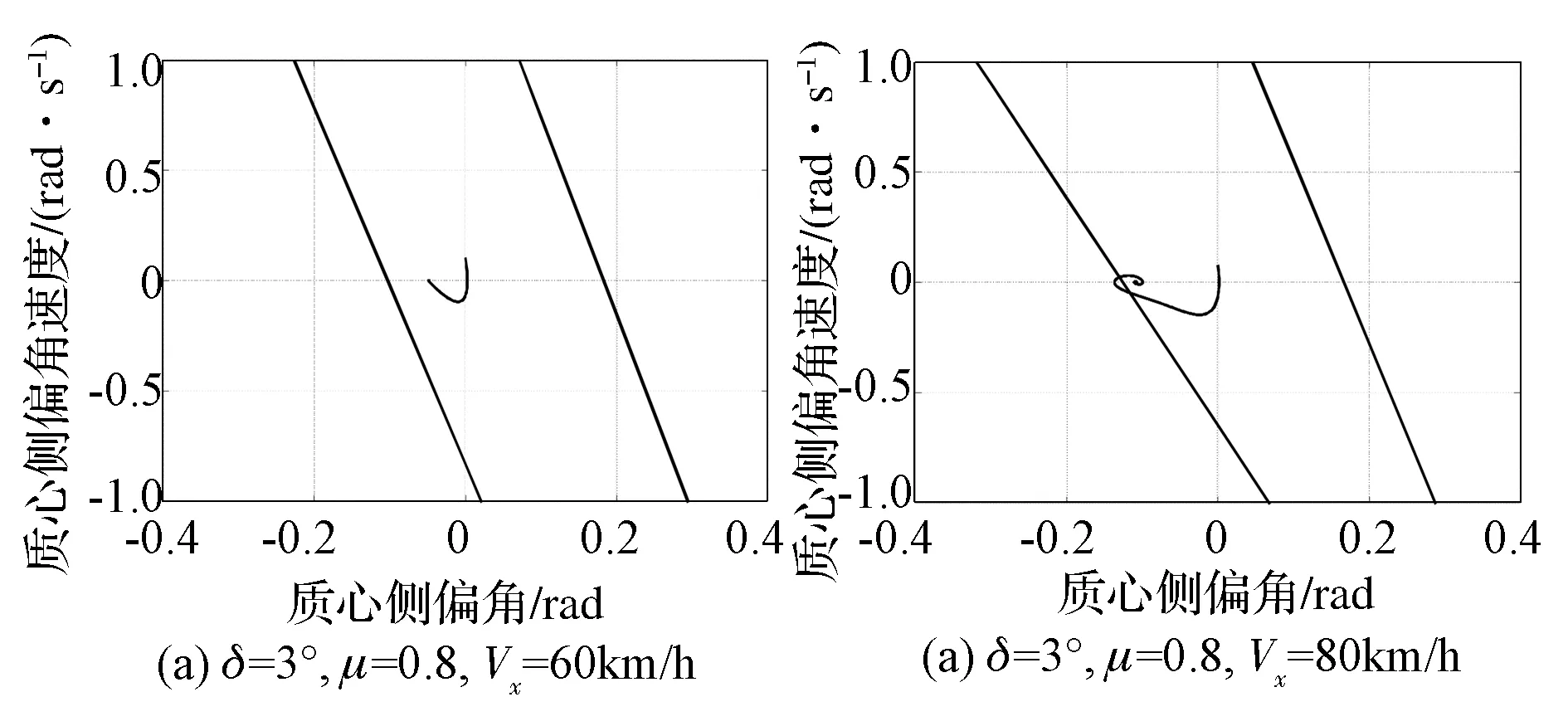
图4 不同车速下稳定边界

从图4(a)可以看出，当车速为60km/h时，车辆自身质心侧偏角-质心侧偏角速度轨迹曲线处于稳定边界内，此时车辆处于稳定状态。从图4(b)可以看出，当车速为80km/h时，车辆自身质心侧偏角-质心侧偏角速度轨迹曲线超出了左侧稳定边界，此时车辆进入了不稳定状态。为确定该行驶条件下车辆的极限车速，可认为某一车速下车辆自身轨迹刚好处于稳定边界内的速度为此时的极限车速。通过小范围减小速度，最终得到轨迹曲线正好处于边界时的临界速度为72km/h，因此判断在前轮转角3°，路面附着系数为0.8的情况下车辆稳定的极限车速为72km/h。利用此方法在不同行驶条件下进行分析，考虑到冰雪路面附着系数约为0.3，沥青路面附着系数约为0.9，因此取路面附着系数的变化区间为[0.3，0.9]。 取前轮转角变化区间为[2°，8°]，若取转向系统转向比为20∶1，则此区间可覆盖转向盘转角区间为[40°，160°]，基本包括了车辆高速转向行驶时驾驶员操纵转向盘的可能情况。得到稳定极限车速、前轮转角和路面附着系数的关系，如图5所示。

根据图5的Map图，在已知前轮转角和路面附着系数的情况下，即可得到车辆的稳定极限车速，为之后的控制策略设计打下基础。

图5 全行驶条件稳定车速

3 稳定性控制系统设计

3.1 控制变量名义值计算

车辆质心侧偏角和横摆角速度与车辆稳定性有着最直接的关系。汽车在正常的行驶状态下，其质心侧偏角与横摆角速度应该与转向盘的转角成一定的线性关系:

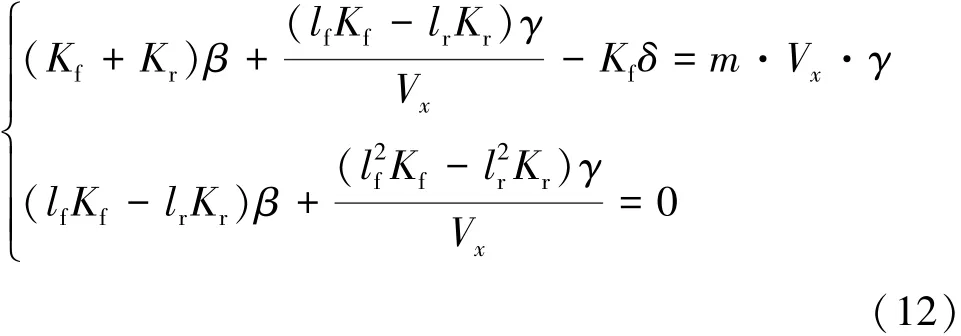
假设驾驶员驾驶车辆做等速圆周运动，联立消元并结合路面附着条件计算横摆角速度理想值:

3.2 控制变量实际值获取与估计

在实际运用中，横摆角速度值可由传感器直接测得，质心侧偏角由其他车辆参数估计得到。结合车辆动力学分析，有

设系统状态变量为

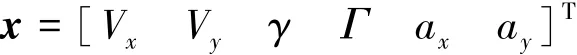
利用轮速传感器很容易估计出车速，利用加速度传感器可测得车辆纵向、侧向加速度，因此取系统观测变量z＝[axayγ Vx]T，可代入扩展卡尔曼滤波方程对状态变量进行估计[11]，再由β＝Vy/Vx估算质心侧偏角。

3.3 模糊控制器设计

运用模糊控制理论设计控制器。以横摆角速度与理想横摆角速度差值e(γ)、质心侧偏角与理想质心侧偏角的差值e(β)作为输入，补偿横摆力矩ΔM为输出。e(γ)和e(β)基本论域为[－0.12，0.12]和[－0.2， 0.2]，量化后论域都为[－6， 6]。 设计的模糊控制流程图如图6所示。

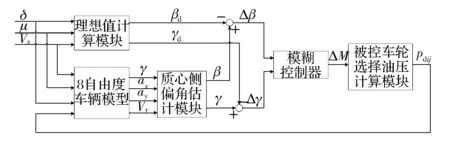
图6 模糊控制流程图

通过大量仿真结果可建立模糊控制规则表，输入输出语言变量的模糊子集均为{PB，PM，PS，ZE，NS，NM，NB}，代表从正大到负大，模糊控制表如图7所示。

图7 模糊控制表

3.4 单侧车轮制动力矩分配策略

通过模糊控制器计算得出所需补偿力矩后，需要考虑对车辆施加同样大小的补偿横摆力矩，从制动系统角度出发，4个车轮的制动都会产生不同方向、不同大小的补偿力矩。以左前轮为例，当车辆左转向时，若对左前轮施加制动力矩，可等效为施加一个向后的力Fbfl，此时该力沿x轴的分量Fbflx和沿y轴的分量Fbfly产生的横摆力矩的代数和即为该制动力矩所能产生的补偿横摆力矩:

同理有制动左后轮可产生补偿力矩为

从式(17)和式(18)可以看出，前后车辆制动时制动力臂有所不同，为防止控制时某一车辆制动油压过大，本文中采用前后车轮比例制动的控制策略，将模糊控制器计算得到的补偿横摆力矩比例分配给前后轮，保证车辆行驶稳定性。同时这也减小了各车轮所需制动油压大小，更利于提高系统使用寿命，且在一条管路出现故障时，仍能保证系统对车辆有很好的控制效果。具体制动车轮选择见表2。

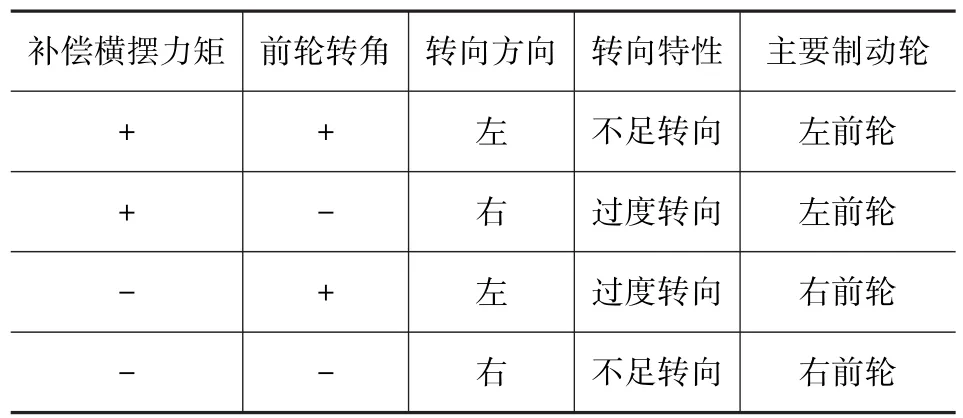
表2 制动车轮选择表

根据上述被控车轮选择表，结合模糊控制器计算得出的补偿力矩ΔM，可得到当需要时施加于某一车轮上的制动力矩:

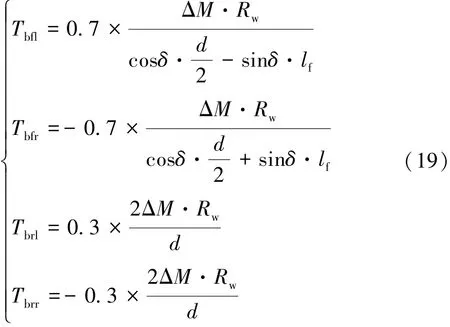
根据上述控制策略，结合车辆极限稳定车速计算，得到车辆稳定性控制系统控制流程图，如图8所示。

4 仿真计算与分析

对上文所述系统在Matlab/Simulink中进行仿真，采用某车型参数(表3)，在容易失稳的低附着路面上对阶跃转向工况和正弦转向工况进行仿真，控制策略开关分别使用基于本文中所述的极限车速控制开关和目前普遍使用的基于横摆角速度控制开关。横摆角速度控制开关在 γ－γd≥ c·γd时起控，其中c为经验常数[12]。

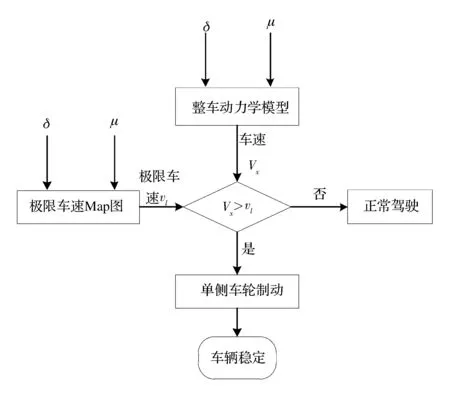
图8 控制系统控制流程

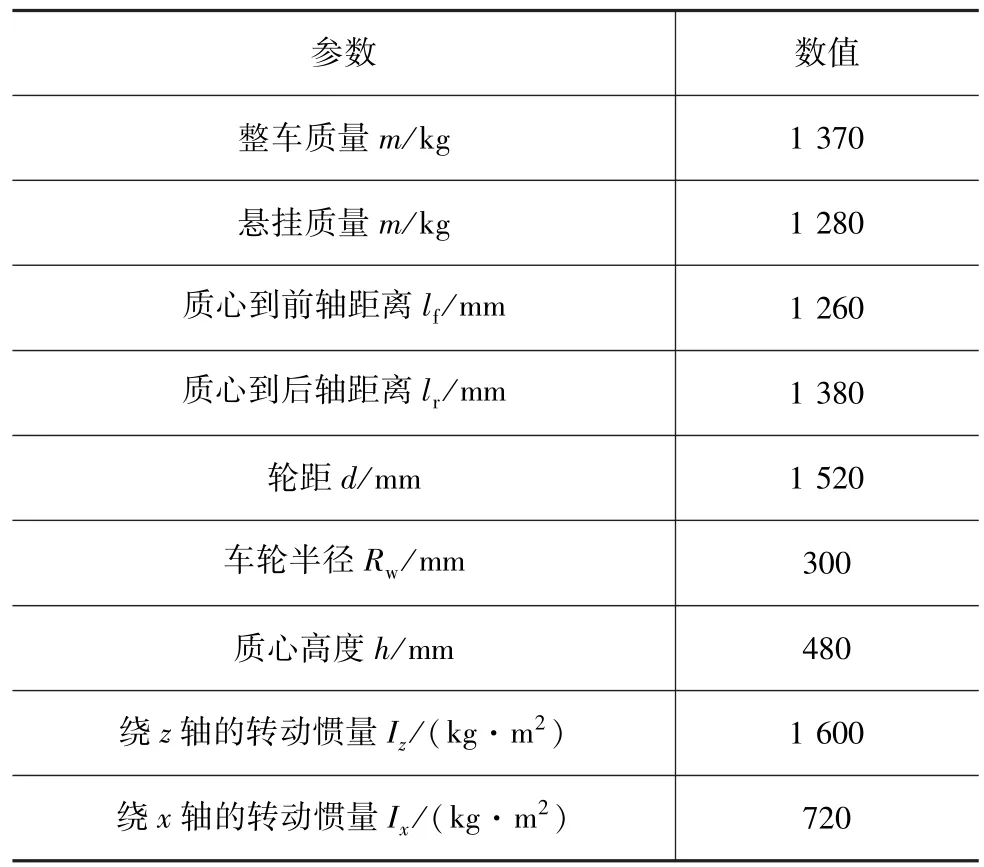
表3 车辆主要参数

4.1 前轮阶跃输入

仿真工况:初始车速70km/h，路面附着系数0.3，前轮转角0.05rad即3°，仿真结果如图9所示。

从图9中可以看出，无控制时车辆质心侧偏角超过0.2rad即12°，在低附着路面上必将出现危险，而施加控制后，横摆角速度可有效跟随理想值；同时，与基于横摆角速度的传统控制方法相比，本文中提出的基于极限车速的控制策略控制后的横摆角速度更贴近理想值，质心侧偏角更小，从而保证了驾驶员对车辆的操纵性，证明了利用极限车速作为控制开关控制效果更好。同时也说明利用单侧车轮制动控制在低附着路面条件下可有效增强车辆行驶稳定性。

图9 前轮阶跃输入控制效果

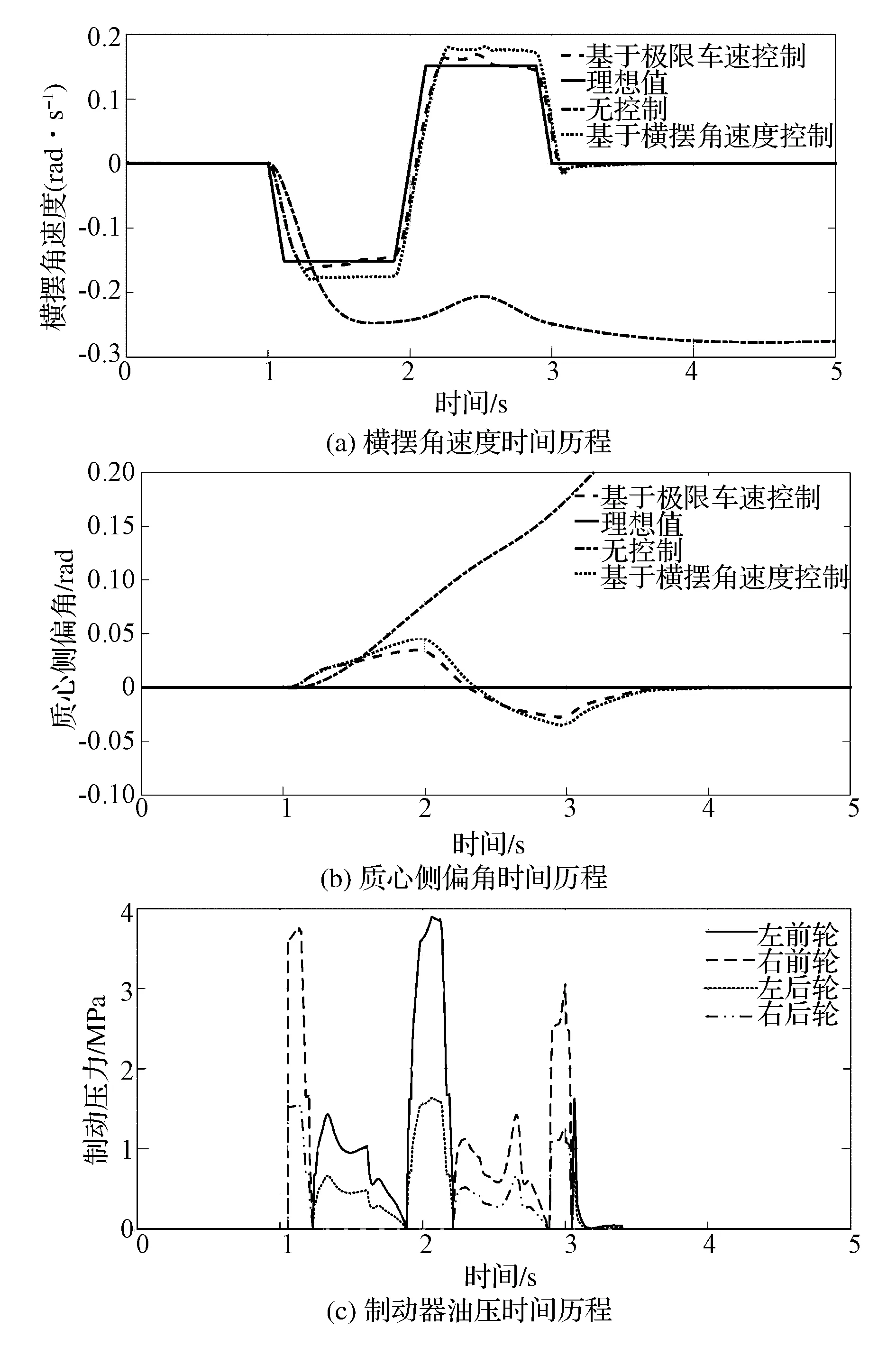
图10 前轮正弦输入控制效果

4.2 前轮正弦输入

仿真工况:初始车速为70km/h，路面附着系数为0.3，正弦输入峰值为0.05rad即3°。仿真结果如图10所示。

从图10可以看出，在无控制时车辆严重失稳，驾驶员丧失操纵性。在施加控制后，横摆角速度贴近理想值，质心侧偏角小于3°，同样基于极限车速的控制方法控制效果要优于传统控制方法，这也进一步说明该控制策略可有效控制车辆完成相应行驶工况，且控制效果良好。

5 模拟驾驶平台实验

驾驶员操纵车辆情况对于车辆稳定性有很大的影响，为使驾驶员对车辆实时可控，同时保证实验的安全性，采用模拟驾驶台架进行实验。模拟驾驶平台由高性能工作站和外部交互设备组成，如图11所示，而其工作流程如图12所示。。

图11 模拟驾驶平台实物图

图12 控制系统控制流程

驾驶员通过外部硬件如转向盘、加速踏板和制动踏板等操纵车辆，外部硬件通过传感器接收到驾驶员的操纵信息后，通过UDP接口将信号输入给工作站的Simulink模型进行计算，随后Simulink中的整车动力学模型结合这些输入信号计算得到车辆位置信息，如纵向位移、侧向位移和航偏角等，再将这些位置信息通过UDP接口传输给Vizard软件，由Vizard软件将这些位置信息与建立的虚拟环境场景和虚拟车辆相结合，以图像的形式显示在显示器上，从而反馈给驾驶员进行车辆操纵。利用模拟驾驶平台进行双移线实验和蛇行穿杆实验对控制策略进行驾驶员在环实验验证。

5.1 双移线实验

在低附着路面上进行双移线实验，实验规范参见ISO 3888-1-1999。初始车速为60km/h，路面附着系数为0.3，实验得到状态参数响应曲线，如图13所示。

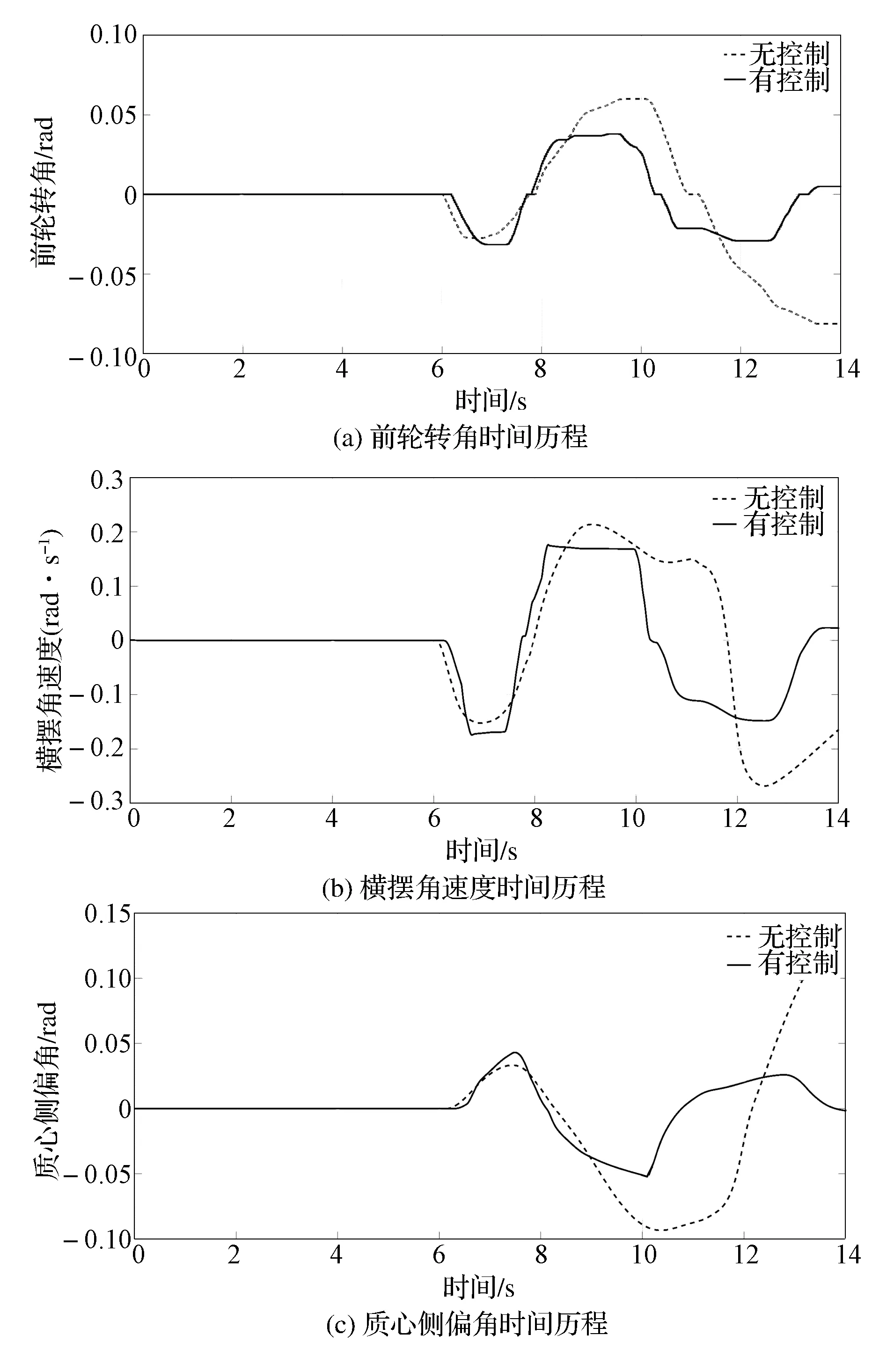
图13 双移线实验工况

从图13可以看出，无控制时驾驶员失去了对车辆的操控性，而施加控制后驾驶员以较小的转向盘转角即可控制车辆完成避障。无控制时车辆横摆角速度从第10s开始就已无法随前轮转角变化而变化，而施加控制后，车辆横摆角速度很快收敛。从质心侧偏角对比曲线来看，无控制时质心侧偏角超过0.11rad即7°且不断增大，而有控制时车辆质心侧偏角峰值小于0.05rad即3°。因此可以看出，该控制策略在低附着路面上能大幅提升车辆稳定性，使车辆在较高车速下仍能够按驾驶员期望的轨迹正常行驶。

5.2 蛇行穿杆实验

在高附着路面上进行蛇形穿杆实验，实验规范参见GB/T 6323—2014。初始车速为80km/h，路面附着系数为0.8，结果如图14所示。

图14 蛇行穿杆实验工况

从图14可以看出，无控制时驾驶员须大幅转动转向盘，且有一桩漏过，施加控制后驾驶员可很好地操纵车辆完成绕桩实验。从质心侧偏角对比曲线来看，无控制时质心侧偏角峰值超过了10°，而有控制时车辆质心侧偏角小于0.05rad即3°，这也进一步证明该控制策略可有效提高车辆稳定性。

6 结论

(1)运用根据相平面法分析得出的车辆极限车速设计的模糊控制器可很好地控制车辆横摆角速度和质心侧偏角，与无控制车辆相比，该控制方法有效提高了车辆操纵稳定性，与传统的基于横摆角速度控制开关的控制方法相比，该方法控制效果更为理想。同时本文中提出的极限车速也可进一步用于驾驶辅助系统中定速巡航的开发。

(2)基于单侧车轮制动的前后轮制动力矩比例分配控制策略能有效实现补偿横摆力矩的分配，减轻了各个制动器制动油压负载，有利于延长其使用寿命。

[1] ZHANG R，HUANG H，CHEN W，et al.Coordinated control of EPS and ESP based on function allocation and multi-objective fuzzy decision[J].Journal of Mechanical Engineering， 2014， 50(6):99-106.

[2] NOBUYUKI Ueki， JUN Kudo， TOSHIO Takayama， et al.Vehicle dynamics electric control systems for safedriving[J].Hitachi Review，2004，53(4):222-226.

[3] YOUSSEF A Ghoneim，WILLIAM C Lin，DAVID M，et al.Integrated chassis control system to enhance vehiclestability[J].Int.J.of Vehicle Design， 2000，23(1-2):124-144.

[4] CHEN Wuwei， XIAO Hansong， LIU Liqiang， et al.Integrated control of automotive electrical powersteering and active suspension systems based on randomsub-optimal control[J].Int.J.of Vehicle Design， 2006，42:370-391.

[5] SHIBAHATA Y，SHIMADA K，TOMARI T.Improvement of vehicle maneuverability by direct yawmoment control[J].Vehicle System Dynamics， 1993， 22(5-6):465-481.

[6] HIEMER M.Model based detection and reconstruction ofroad traffic accidents[D].Kalsruhe:Kalsruhe University，2005.

[7] GUO K.A study of a phase plane representation forIdentifying vehicle behavior[J].Vehicle System Dynamics， 1985， 14(1-3):152-167.

[8] BAKKER Egbort， NYBORG Lars， PACEJKA Hans B.Tyre modeling for use in vehicle dynamics studies[C].SAE Paper 870421.

[9] BARDAWIL C，TALJ R，FRANCIS C，et al.Integrated vehicle lateral stability control with different coordination strategies between active steering and differential braking[C].Intelligent Transportation Systems(ITSC)，2014 IEEE 17th International Conference on.IEEE，2014:314-319.

[10] CHUNG T，YI K.Design and evaluation of side slipangle-based vehicle stability control scheme on a virtualtest track[J].IEEE Transactions on Control Systems Technology，2006，14(2):224-234.

[11] HSLECH F C.Sideslip angle estimation using extended Kalmanfilter[J].Vehicle System Dynamics， 2008， 46:353-364.

[12] GAO Zhenhai，WANG Jun.Multi-control states and switch conditions design for vehicle electronic stability program[J].Journal of Mechanical Engineering，2014:107-119.