基于层次分析法的满意度评价模式
许灵波 董忠泽

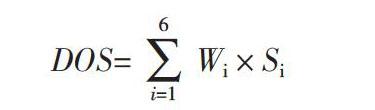
摘 要:《机关事业单位党组织星级评定参考标准》规定,党员群众和服务对象测评满意度低于50%的党组织,直接定为“无星”,文章探讨如何利用层次分析法定量评定高校服务型党组织创建星级评定满意度,为基层党组织分类定级工作提供理性的参考依据。
关键词:服务型党组织;层次分析法;评价模式
高校服务型党组织研究创建满意度评价模式的目的是为各基层党组织探讨适合自己支部的服务型党组织建设提供依据,本文高校服务型党组织创建满意度评价模式的每个评价指标都经过客观分析,使评价的结果具有科学性。各个支部的情况不尽相同,在上级党组织的一套标准之下,各个基层党组织应该根据自身特色,就上级党组织的统一指标的各项权重进行科学分析,以便各项判断更具有科学参考性。
一、层次分析法原理
层次分析法是美国运筹学家托马斯·塞蒂所创建的一种分析方法,该方法将定性分析与定量分析相结合,将目标拆分成多个因素,通过在各个因素之间两两比较,最后得出不同因素的权重,从而为最佳选择提供理论参考依据。
二、高校服务型党组织创建星级评定满意度评价模式的构建
(一)高校服务型党组织创建星级评定满意度评价模式指标确立
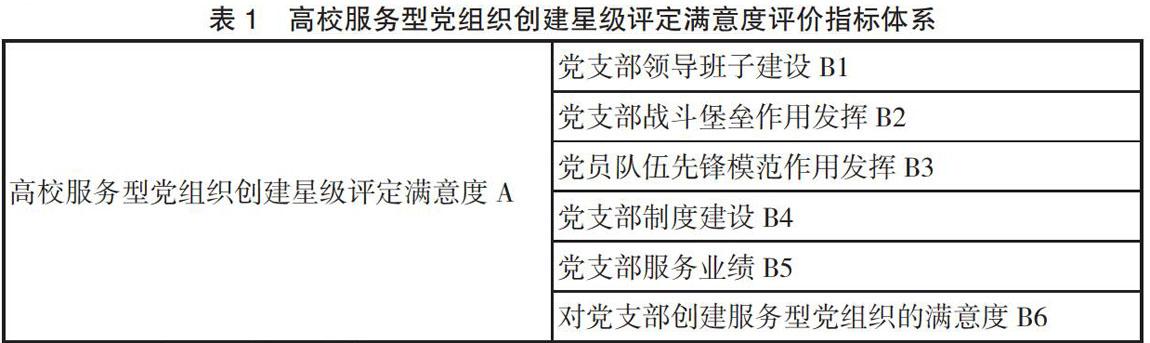
本文根据《中共中国计量学院委员会关于推行五星级管理深化服务型党组织建设活动的实施意见》文件要求,将党员群众和服务对象对服务型党组织创建星级评定满意度细分为党支部领导班子建设、党支部战斗堡垒作用发挥、党员队伍先锋模范作用发挥、党支部制度建设、党支部服务业绩、对党支部创建服务型党组织的满意度等6个一级指标。
(二)高校服务型党组织创建满意度评价模式的层次评价
1.构建两两比较矩阵
根据已经建立好的服务型党组织创建星级评定满意度评价指标体系(見表1),通过比较影响同一准则的各因素之间的重要性,构造比较判断矩阵。假定准则A与下一层次中的因素B1、B2…、Bn有关,那么构造的判断矩阵如表2所示。其中,Bij的含义是Bi对于Bj的相对重要性。相对重要性的大小采用托马斯·塞蒂的1~9标度法(见表3)。矩阵满足:Bij>0;Bii=1;Bij=1/Bji(i,j=1、2…n)。
2.每层指标的相对权重及其一次性检验
高校服务型党组织创建星级评定满意度评价各指标重要性不相同,为了减少人为因素的影响,本次判定综合了5名专家评分意见。各层次相对于上一个层次的权重向量如表4所示。通过Python的Numpy模块,计算各指标权重和最大特征根λmax。
由于测评服务型党组织创建星级评定满意度的相关因素具有多样性特点,且评分专家对各项指标的认识不同。因此,在构造判断矩阵会存在偏差。层次分析法为了避免人为因素引起的重大偏差,将对构造的判断矩阵进行一致性验证。一致性的指标CI的计算方法为,CI=(λmax-n)/(n-1),CI的值越大,矩阵的一致性越差,CI与RI的比率称为检验系数CR,只有当CR<0.1时,这个矩阵的一致性才是可靠的。如表5所示,本次测评的CR为0.054,小于0.1,证明该矩阵的一致性符合要求。
三、高校服务型党组织创建星级评定满意度评价模式的实例
(一)数据获取
本文选取中国计量大学继续教育学院党总支作为高校服务型党组织创建星级评定满意度的评估对象。选取教工党员15名、学生党员5名、教工群众5名、学生群众5名作为测评者,以6项指标为基准,每个问题都有四个选项,分别是好、较好、一般、较差,在处理数据时分别对应100分、75分、50分、25分。
(二)数据处理
30名测评对象独立对6项指标打分,取平均值作为该项的Si,具体结果见表6。根据权重,综合测评对象打分Si,得到服务型党组织创建星级评定满意度测评结果,计算公式为:
公式中,DOS(Degree of satisfaction)为服务型党组织创建星级评定满意度测评结果,Wi为第i项评价指标的权重(见表5),Si为测评对象给出的第i项的打分,DOS的值越大,该支部的服务型党组织创建星级评定满意度越高。
(三)结果分析
如表6所示,中国计量大学继续教育学院党总支在服务型党组织创建星级评定中,党员群众和服务对象对该总支的满意度较高,得分为92.289(百分制计分),远远高于50%,符合定星的基本准则。同时,在该总支的满意度评价的6个一级指标中,权重最大的是领导班子建设,占比31.6%,最小的是党员队伍先锋模范作用发挥,占比7.7%,这个基本符合该总支的状况。该总支领导班子齐全,内部团结,致力于做好党员发展及党员队伍建设工作。但是鉴于学生党员规模小的原因,总支的党员人数不足20人,整个党员队伍数量小,因此在6个一级指标中,党员队伍的先锋模范作用发挥的权重必然相应较小。
参考文献:
[1]马天威,任 鹏.论全面从严治党视域下高校基层党组织实干精神的强化[J].东北大学学报(社会科学版),2017(5):533-538.
[2]李亮林.新形势下高校服务型基层党组织建设存在的问题及对策研究[D].重庆:重庆师范大学,2017.
[3]邓 雪,李家铭,曾浩健,等.层次分析法权重计算方法分析及其应用研究[J].数学的实践与认识,2012(7):93-100.

