基于复杂网络模型的供应链企业合作演化研究
,
(兰州交通大学a经济管理学院; b交通运输学院,兰州 730070)
0 引言
近年来,随着全球经济一体化发展和贸易改革的不断深化,市场的需求呈现多元化发展趋势,企业所面临的内外部环境也日趋复杂,以利益最大化为目标的成员企业之间的竞争愈演愈烈,供应链管理问题日益严峻。并且,随着科学技术与人们对产品质量要求的提升,企业间的竞争合作关系已经提升到供应链网络阶层,供应链网络逐渐呈现出复杂网络的特征。
在上述情况下,一切有合作关系的企业之间便可能会结成联盟,从而加强企业之间的联系,改变供应链网络的结构和特性。因此,供应链网络结构的发展既有规律性,又掺杂着随机性,无法用标准的规则网络或是随机网络来解释供应链网络,而复杂网络理论却能恰当地反映供应链网络动态演化特征[1]。并且,随着计算机科学的发展和复杂系统研究的深入,复杂网络理论得到了进一步的发展。
本文在分析复杂网络供应链合作演化的国内外研究基础上,基于复杂网络理论,分析了无标度网络BA模型,并结合供应链网络的特性对BA模型进行了改进,得到了基于供应链网络度值分布的网络演化模型,即双段幂律分布模型,进而分析供应链网络上企业的合作演化关系,为供应链网络上企业的管控与优化提供了参考资料。
1 国内外研究现状
近年来,随着复杂网络理论的发展和供应链网络的复杂化,许多国内外研究学者从复杂网络的角度来剖析供应链网络上企业间的竞争合作关系与其发展演化规律,但该类研究仍处于起步阶段。
早在1999年,Barabási等人[2]就提出了增长和择优连接是形成无标度网络的机制,并将连续化方法引入到了复杂网络研究中,从而得出了著名的适用于无标度网络的BA模型。此后,基于复杂网络的研究进入发展高潮。在供应链网络复杂性研究方面,2017年,范碧霞等人[3]首先对复杂网络的特性进行了描述,然后剖析了复杂性产生的内在机制,并认为复杂网络理论可以有效地帮助评价和管理供应链。2018年,丁飞等人[4]在BA网络模型的基础上引入反择优概率,构建了包含节点进入、退出和合作的网络模型,并利用仿真验证了模型有效性。2005年,Venkata等人[5]利用基于演化的自组织理论方法阐述了供应链的复杂网络结构特征、节点成员企业与系统目标之间的联系,并通过仿真分析了供应链网络的复杂结构特性。
而在供应链网络节点度值分布和动态演化研究方面,Pathak[6]指出供应链是一个典型的复杂适应系统,研究了供应链网络的生长、涌现机制和其影响因素,从而分析供应链网络的动态演化过程。2012年,葛伟等人[7]在局域世界演化模型的基础上,引入节点相关度来作为衡量一个节点与网络中其他节点间相近程度的指标,定义局域世界的整体规模是动态变化的,进而建立了供应链系统的局域演化模型。2013年,傅培华等人[8]经过具体分析供应链网络的动态演化特性,提出了一种基于度值与连边优先连接的集聚性供应链网络演化模型。2014年,吴义生[9]基于系统动力学理论,构建了低碳供应链协同运作的演化模型,并根据自组织原理分析了序参量对于低碳供应链协同运作的影响。2016年,曹文彬等人[10]将供应链企业合作所带来的边际效益与复杂网络相结合,然后利用节点度和边际效益因素构建了复杂供应链网络局部演化模型,并利用仿真进行了模型验证分析。2016年,孙军艳等人[11]从复杂自适应系统角度利用Agent仿真分析了轿车供应链的网络特征,并对轿车供应链系统的非线性特性、各Agent和网络整体的演化规律进行了仿真分析。2017年,于淼和马军海[12]从制造商与零售商层面建立了一个回收废旧电子产品的闭环供应链模型,运用博弈论、混沌动力学和复杂动力学理论并结合数值实验得出调整参数可以对混沌进行了有效的控制。2017年,张学龙等人[13]利用链路预测方法,并结合5种指标对能源供应链网络的连边演化预测进行了分析,并通过实验得出链路预测在分析供应链网演化时比直接建立模型分析更有效。2018年,丁飞[14]基于BA网络模型构建了一种包括节点进入、退出和补偿机制的供应链网络演化模型,得出节点的度分布服从幂律分布。2018年,李柏洲等人[15]在引入基于时间度和前景理论的直觉模糊妥协评价模型基础上,考虑了合作创新资源互补性,运用场理论构建了伙伴动态选择的合作创新能力场模型。
综上所述,目前大多数有关供应链网络的研究主要是基于控制理论、系统仿真和供应链协调机制等方面展开的,而面向复杂网络对供应链管理进行的研究还处于起步阶段。因此,本文先是分析了国内外供应链网络演化的相关研究,并基于BA模型和泊松更新过程理论建立了改进的供应链网络演化模型,从而以复杂网络的角度探究了供应链企业间的合作演化关系。
2 复杂网络环境下基于双段幂律分布的合作演化模型
以往复杂网络BA模型的增长机制都是假设节点是等时间间隔离散地进入系统,但是在现实的复杂供应链网路中节点是随机到达的。为了弥补上述模型存在的不足,更深入地在微观层面中探索影响复杂网络拓扑和演化的各种因素,本文引入双段幂律分布,可以更为准确描述供应链网络中节点进入系统的随机性,供应链网络从一个不完备的状态向一个相对理想的状态演化过程中所呈现的特征,以及如何对参量进行控制,使得供应链网络从无序向有序进行转化。
2.1 双段幂律分布
幂律分布特性在无标度复杂网络的各项研究中非常普遍,是自组织临界系统在混沌边缘,即从稳态过渡到混沌态的一个标志。然而在某些情况下,这样单一的属性不能充分地描述现实世界系统的分布规律,此尺度理论在有些领域是不充分的。
而在幂律分布中,把包含两段不同幂律区域的分布称为双段幂律分布,其累计分布由变量K来表示,K值大于一个特定值k,如下:
(1)
其中,γ1与γ2为两段幂律分布指数,kc为双段幂律分布中的转折点。这一分布特性广泛存在于社会经济系统中,如中国航空网的度分布、语言网络、科学家合作网及人们的收入分布网络等。非广延统计理论和不同幂律函数的组合被用来解决这个问题。为了了解其内在的机制,Reed基于几何布朗运动提出了一个模型,证明了这一过程耦合了指数分布的演化时间。双帕累托(Pareto)对数正态分布尽管是对数正态的主体,但是在两尾上均具有幂律行为。这一分布非常符合收入分布的实际数据。Dorogovtsev与Mendes提出了另一种模式旨在解释语言网络中度分布的双段幂律特征[16]。这一模型中包含两种机制,一种是偏好依附机制,另一种是随着时间演化,基于已经存在的节点建立新连接。进一步发现度分布具有两个不同的幂指数,高尾是-1.5,低尾是-3。尽管上述两个模型分别描述了收入分布网络与语言网络的两种情况,但是都存在局限性。在语言网络中,幂指数是固定不变的,因此无法解释为何存在不同的幂指数。而Reed模型假设收入的相对增长率对于全部的人群是一样的,远远不符合人们赚钱能力不同的实际情况,因此,为得到普适的模型,必须考虑适应度的因素。
此外,有些与双段幂律相关的工作更注重通过用一个统一的函数来表述这一分布,而非将两段幂律独立地看待。本文用一种通用的随机模型来解释双段幂律分布的现象。该模型同时考虑了适应度与噪声涨落两个方面,可以通用地描述许多现实世界系统的演化,相对经典的幂律而言,双段幂律分布更符合企业供应链发展演化的特点,因此,本文基于双段幂律分布建立了供应链网络演化模型。
2.2 供应链网络演化模型分析
在实际情况下,供应链网络的初始规模很小,各网络节点的度值较低,但供应链网络会随着时间的推移在自组织规则下演化成复杂网络系统,而复杂网络供应链会表现出显著的复杂性和动态性。下文将进行具体分析。
2.2.1 供应链初始网络模型条件及演化特征
为了更有效地表征实际供应链网络,客观上对初始网络模型提出3个条件:
1)具有较好的增长机制;
2)原有企业节点退出后,与之相关联的节点会进行网络重构;
3)在企业节点相连接时,更偏向于业务范围广和规模大的网络节点企业,即符合富者越富的正反馈现象,度量标准为节点的度重要性,如式(2):
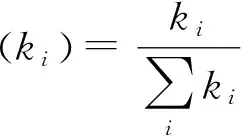
(2)
在初始供应链网络从无序向有序转变的演化过程中,网络系统也由混沌状态逐渐向协同稳定状态转变,并且考虑了成员企业间业务关系随外部运作环境及时间的变化。在外部环境和内部关系相互作用下,供应链网络会逐渐凝聚成员企业及它们之间相互作用的变化,从而涌现到新的演化阶段。在整个网络演化过程中体现出以下3点特征:一是择优连接机制,加入供应链网络的新企业在选择建立业务的网络既有企业时,会优先挑选网络节点企业中规模大、度值高的节点。二是局域选择机制,新加入的企业节点只能选择与其邻接的上游供应商企业和下游制造商企业相连接,故在供应链网络演化期间,需要先确定企业类型,再在邻接范围内择选合适的企业进行连接。三是偏增长性机制,供应链网络在演化过程中,既有新企业建立的新关系,又产生旧企业退出截断的旧联系,演化过程为偏增长性。
2.2.2 供应链网络演化理论及演化步骤
在初始供应链网络随时间动态演变的过程中,遵循自组织理论和人类动力学理论。自组织是一个系统通过与外界交换物质、能力和信息来降低自身的熵值,受内在机制影响,自行地从简单向复杂、从粗糙向细致方向发展演化,不断提高自己结构的有序度和自适应、自发展功能的过程[17]。而人类动力学理论认为人们在处理各类事物时,通常对各类事物的优先级进行划分,首先处理高优先级的事物,这种行为模式是导致幂律分布的重要原因[18]。
供应链网络演化的具体步骤如下:
1)根据实际情况,分析复杂网络总节点以及连边数的增长规律,求解复杂网络中度分布的相关参数,幂指数γ1、γ2、转折点kc;
2)新的变量以初始值1按照指数分布加入复杂网络系统中,赋予的适应度则以正态分布取值,然后每一个变量按照Nt∝ecnt进行增加,从而得到网络演化过程中的适应度的均值和标准差;
3)求解涨落的标准差以及噪声与适应度相对作用的参数ρ,并得到不同参数ρ下的累计分布;
4)由步骤2)、步骤3)得出的服从正态分布的适应度和涨落标准差,与演化时间有关的斜率eat,求解微分,得到双段幂律分布模型的准确形式;
5)用步骤4)中的模型准确形式模拟仿真度分布,得出两段的幂指数γ1、γ2,与步骤1)中的参数进行对比。
2.2.3 供应链网络演化模型参数解析
本文拟建立供应链网络演化模型来对供应链网络的演化过程进行描述,并通过控制一些相关的关键指标参数,如幂指数γ、适应度η和影响程度参数ρ等,来更加准确地对演化过程进行控制,对演化结果进行解释。
由前文可知,供应链网络演化模型服从幂律分布,但其幂指数γ在不同演化时期会有所不同。当γ增大时,供应链网络规模分布概率减小,说明网络中节点度值较大的企业数量在减小,同时企业规模的差异缩小。而当γ减小时,说明网络中节点度值较大的企业数量增多,网络企业节点度值分布更加离散。但幂指数γ的值不会无限减小,受适应度η和外部因素的制约,企业节点度值也不会无限扩大,幂指数γ最终会收敛于某一个大于0的常数,达到稳态分布。其中,适应度η代表自身一些属性,在供应链网络中适应度可以理解为节点企业的资本、机构等级、规模和所属行业等。而参数ρ代表了主导因素对演化影响的程度大小,若演化过程完全被主导因素所控制,则ρ→1,网络演化的过程是一个确定的模式;若没有明显的主导因素,则ρ→0,演化过程则呈现一个随机的状态。
下面将主要从适应度耦合与噪声涨落动力学两个方面详细阐述供应链网络演化模型。
3 模型描述
3.1 适应度耦合分析
3.1.1 模型条件设定
为了更为清楚地描述供应链网络中节点进入系统的随机性和灵活性,本文假设kit,t1为第i个变量在t时刻的值,并在t1时刻进入系统,定义N(t)为在t时刻系统中变量的总数。在自组织复杂网络系统中,由于偏好依附机制的影响,ki的增长率与其自身的值成一定的比例关系,且与自身的一些属性有关,本文将这些属性统称为适应度ηi,除此之外,度值还可能被其他一些随时间变化的因素所影响,但首先考虑简单的情况,即这些因素以常数来表示。kit,t1的演化方程为:

(3)
假设kit1,t1=1,则kit,t1=eηi(t-t1),表明复杂网络的度值呈指数增长,这直接约束了系统中变量总数N(t)的形式,如系统中节点度的演化。因此,指数增长的度值要求N(t)也是指数增长的(甚至增长更快),即假设变量总数按指数增长:
Nt∝ecnt
(4)
正态分布的适应度对于该网络演化模型来说至关重要,它是出现双段幂律现象的必要条件。当在一个复杂网络系统中,为适应度选择一个特定的参数时,系统中变量总数N(t)也会出现相同的问题。由于复杂网络节点的度值不能大于n(t)-1,在网络不断演化过程中适应度应当限制其均值μα不能远大于Cn,而标准差ση应当在适当的范围内。
3.1.2 供应链网络双段幂律分布模型及分析
基于以上模型条件设定,下面对复杂供应链网络的双段幂律分布模型进行详细剖析。由方程Pkit,t1dkit,t1=fηidηi可知kit,t1的分布符合对数正态分布。由于变量以指数增长的速度加入进来,变量的生命时间定义为T=t-t1,符合指数分布。因此认为ki是一个结合于指数分布T的对数正态分布ki(T)。这样该分布可以由式(5)来表示:
(5)
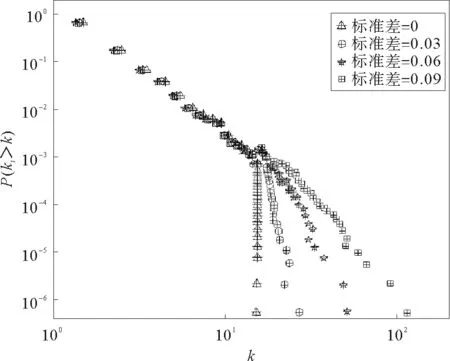
图1 ki的累计度分布Fig.1 The accumulative degree distribution of ki

图2 在tc不同的情况下ki的累计度分布Fig.2 The accumulative degree distribution of ki under different circumstances of tc
其中,tc是考虑p(k)的时刻。如果标准差趋于0,则式(5)可以改写成:
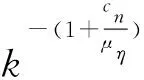
(6)
其中,当k≤0时,ξk=1;当k>0时,ξk=0。
下面需要利用数值试验,来讨论标准差在有限的范围内该模型的分布特征。对于有限的标准差大于0,实验的实现步骤如下:在每一步中,新的变量以初始值1按指数分布加入系统,赋予的适应度则以正态分布取值;然后,每一个变量按照式(4)中的关系增加。对于不同的标准差仿真累积分布,如图1所示,其中,μη=0.15,Nt=50e0.088t,tc=30。
当标准差等于0时,如上文所述,分布服从幂律分布,且极值为最大值。随着标准差的增加,分布的第二段衰减的越来越慢,函数曲线的形状与幂律分布相似。需要指出的是,转折点发生在大约最大值时,此时正是标准差等于0时界限出现的点。因此,转折点会随着演化时间tc而提高,如图2所示,进而得到式(7):
kc~eμηtc
(7)
首先,对双段幂律分布的第一段进行分析。随着标准差的增长,分布的第一段并没有发生显著的变化,从图1中可以看到曲线的第一段与标准差等于0的分布发生了重叠。因此,p(k)的第一段服从同样的幂律分布,该分布的标准差等于0,幂指数如式(8)所示:
(8)
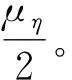
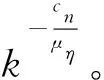
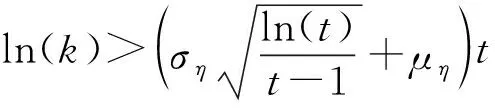
(9)
由于ση通常比较小,不等式(9)的成立条件简化为lnk>μη。对于任何的k>eμηtc,式(9)左边部分从0到tc一定大于右边部分;左边部分正是度分布p(k),右边部分则大致服从一个指数与μη、ση和cn相关的幂律分布函数。因此对上述指数的一个特定组群,p(k)拥有较低的范围。
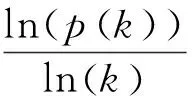
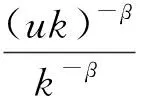
(10)
令β趋于0,则有
(11)
当0<μ≤1时,式(11)也成立。当p(k)满足渐进尺度不变这个条件时,可推知l(k)的上述特性。因此,l(k)仅仅控制供应链网络模型分布中低尾的有限范围,并不能显著地影响其尺度指数。当然p(k)的第二段也服从幂律分布。更进一步的研究表明,数值的仿真可以确定p(k)第二段的幂指数,设为γ2,而
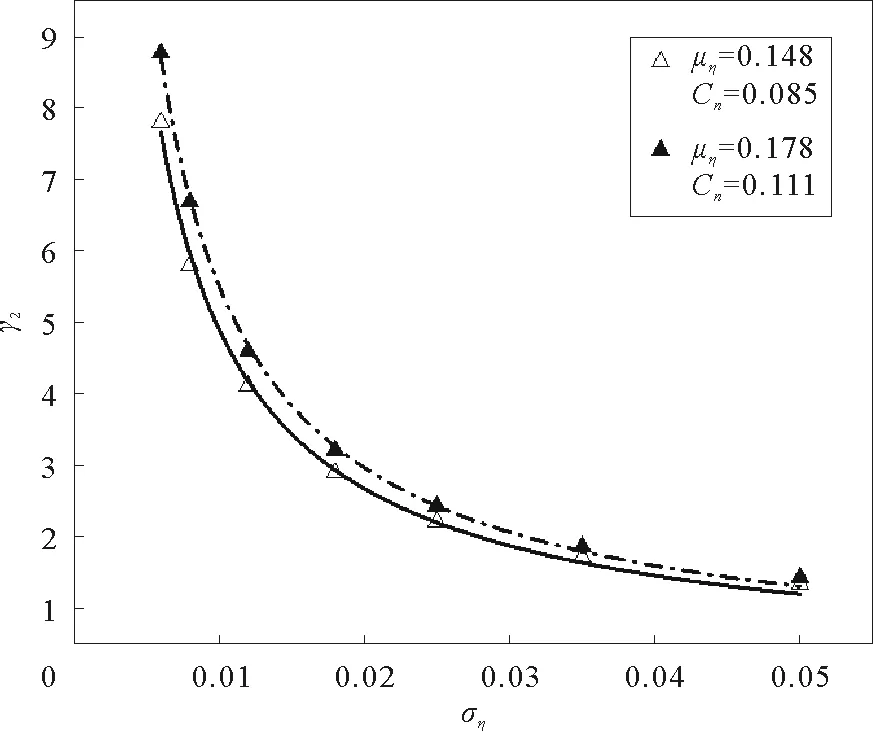
图3 γ2的数据仿真Fig.3 Numerical simulation of γ2
(12)
式(12)仿真结果如图3所示。需要指出的是,当ση→0时,λ2→∞。p(k)的第二部分自然褪变成为界限,γ2的方程同样与cn或μη有关系。大量的仿真结果表明,γ2对参数ση的变化较之cn或μη的变化更加敏感。据此,本文提供了一个可能的模型来实现双段幂律分布。
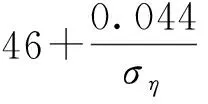
3.2 噪声涨落的演化动力学分析
在现实生活中,供应链网络随时间进化的过程通常包含有涨落特性,这对于其演化的动力学的描述至关重要。因此,一个通用的模型,必须能够描述这一特性。这一通用模型可以从式(3)变化得来:
dki=ρηikidt+1-ρμηdt+σdωki
(13)
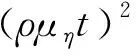
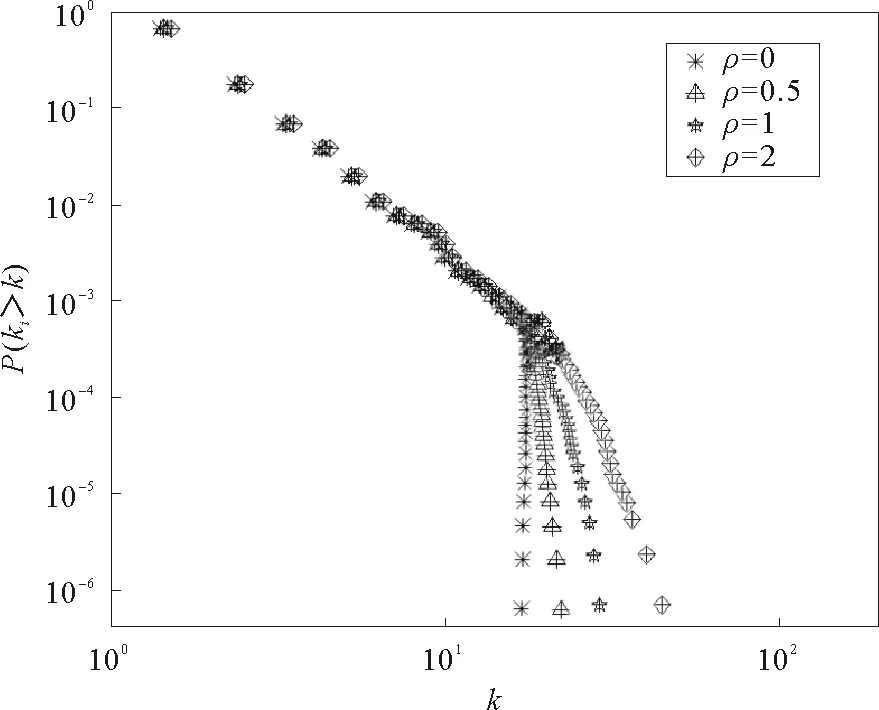
图4 ρ不同时累计分布的仿真分析Fig.4 Simulation Analysis of cumulative distribution of ρ
经过上述对基于双段幂律分布的供应链网络合作演化模型的构建与分析,可以得出在现实生活中复杂网络供应链的演化主要由两个部分构成:一是主导因素,即适应度;二是噪声涨落。因为供应链网络的演化通常与多个因素有关,但是在模型构建与分析中并不能将所有因素都考虑进来,一个可行的方法是将大多数的重要因素作为适应度来考虑,其他稍弱的因素作为噪声涨落来考虑。而参数ρ若趋于1,则复杂系统是确定的模式;若趋于0,则为一个随机的状态。故本文所描述的模型可以较好地用来描述演化处于有序与无序状态之间的复杂网络供应链系统,分析其节点企业之间的合作演化关系,从而更好地为宏观供应链网络的管理与控制提供决策支撑和材料支持。
4 供应链网络演化的实证研究
在一些中国航空网、科学家合作网、语言网络等复杂网络的实证研究中,其度分布均出现了双段幂律行为。在以上模型分析的前提下,本文选用中国汽车制造行业供应链网络为研究对象,分析其复杂的动态演化过程。
汽车制造行业是重要的中游制造行业[20],是一个资本密集型和技术密集型行业,其上游对接零部件、钢铁、橡胶原料企业及生产设备制造业等,中游为汽车整车制造企业,下游则主要对接矿山开采、公路交通运输、特种用途车辆等需求的企事业及用车个人等。汽车制造行业的上、中、下游企业构成一个相互联系的供应链网络,并且由于国家市场经济的浮动性,导致汽车制造行业供应链上的企业间合作关系总是处于动态变化的状态,符合基于双段幂律分布的合作演化模型所用来描述处于有序与无序状态之间的现实复杂系统的应用条件。
4.1 模型参数设定
在中国汽车制造业供应链网络中,以成员企业作为复杂网络中的节点,成员企业间的业务来往作为复杂网络中的连边,节点的度可以定义为连接到该点的所有连边数。
首先,本文在t年分析中国汽车制造业供应链网络上N(t)个节点企业。中国汽车制造业供应链网络按Nt∝ecnt增长,且Cn≈0.079,这与前文供应链网络模型中提及的节点个数以指数规律增长是相符合的。连边数M(t)同样是以指数规律不断增长的,且Mt∝ecmt,而Cm≈0.116。由于现实中完整汽车供应链网络信息的难以获得性,本文选取具有代表性的部分企业进行探讨,得到中国汽车制造业供应链网络共包含296个节点企业和2 377条连边数。
另外,基于2012年至2017年中国汽车制造业供应链网络的实际情况,本文还分析了汽车行业供应链网络的度分布的相关参数,结果如表1所示。从表1可以看出,该供应链网络分布的第一段幂指数γ1数值稳定在大约0.47,而分布的第二段的幂指数γ2则在[1.8,2.5]范围内波动,这与前文所述相符。而参数γ1的稳定则说明了模型中提到的γ1与噪声涨落无关。转折点Kc展示了一个递增的趋势,从15增长到26,这也与模型中提及的转折点随着演化时间增加是一致的。

表1 累积度分布中幂指数γ1与γ2和转折点KcTab.1 Power exponent γ1 and γ2 and turning point Kc in cumulation degree distribution
4.2 模型运行过程和结果的分析说明
在本文中,中国汽车制造业供应链网络演化的研究还涉及企业净利润、净资产收益率与度值之间的相互关系,根据前文模型的描述,将企业净利润和净资产收益率作为对应节点的适应度来进行考虑。度的演化可以通过连续几年的度比值的对数直接进行考量,但是这种方法既不能体现出适应度的作用,也不能给出相应参数的有用信息。因此本文收集到汽车制造行业大约296家公司近五年的净利润以及净资产收益率,并得到中国汽车制造业供应链网络2014年和2017年度分布与企业净利润的关系图以及2014年和2017年度分布与企业净资产收益率的关系图,如图5所示。
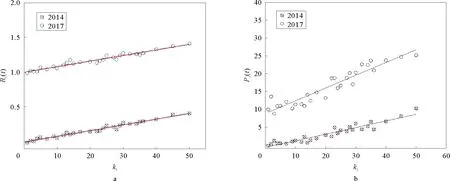
图5 2014年与2017年度分布与净利润、净资产收益率的关系Fig.5 The relationship between distribution and net profit and return on net assets in 2014 and 2017
其中,Ri(t)表示所有具有相同度值k的节点企业的净利润平均值,Pj(t)表示所有具有相同度值k的节点企业的净资产收益率平均值。为了方便观察,图中刻意拉大了2014年和2017年数据的距离(其中Ri(2017)数值在原始数据基础上增加了1个单位;Pi(2017)数值在原始数据基础上增加了10个单位)。从图5可以看到,噪声涨落明显存在,但是度分布在对应企业净利润和净资产收益率的情况下均形成了一个线性函数。自2014年以来,中国汽车制造业企业净利润和净资产收益率与度演化的相互关系持续了至少4年(2014—2017年),随着汽车制造业供应链网络中企业净利润和净资产收益率的增加,供应链网络中度值越小的汽车制造企业存在的概率变得越小。
考虑到汽车制造供应链网络随着时间不断演化,企业成员的净利润和度值之间的相互关系用式(14)进行描述:
(14)
在式(14)中,Rit为成员企业i在年份t的企业净利润值,且Rit呈现指数规律增长,Rit∝eλit,λi服从正态分布,均值为0.18,标准差为0.02。Rit为成员企业i在时间t的企业净资产收益率,且Pit呈现指数规律增长,Pit∝eλit,λi服从正态分布,均值为0.16,标准差为0.01。上述公式证实了企业净利润以及净资产收益率对于汽车制造业供应链网络演化的主导作用。
除了上述主导因素(企业净利润和净资产收益率),其它的作为噪声涨落的弱影响因素同时存在,如市场规模、税收政策、运输条件、劳动力成本、科技创新水平等。所以,以上两方面因素都会对D(t)造成影响,其表达式为
Dt=eateεt
(15)
其中,eat是与时间有关的斜率,而eεt则代表了弱因素(噪声涨落)。a(t)的具体形状可以估计出来,根据式(11)计算所有节点的净利润,可以得到式(16):
(16)
将所有企业总利润以及企业间连接数量代入式(16)可得到a(t)=-0.028t。根据式(13)可得式(17),将εt的增量定义为dεt=εt-εt-1。
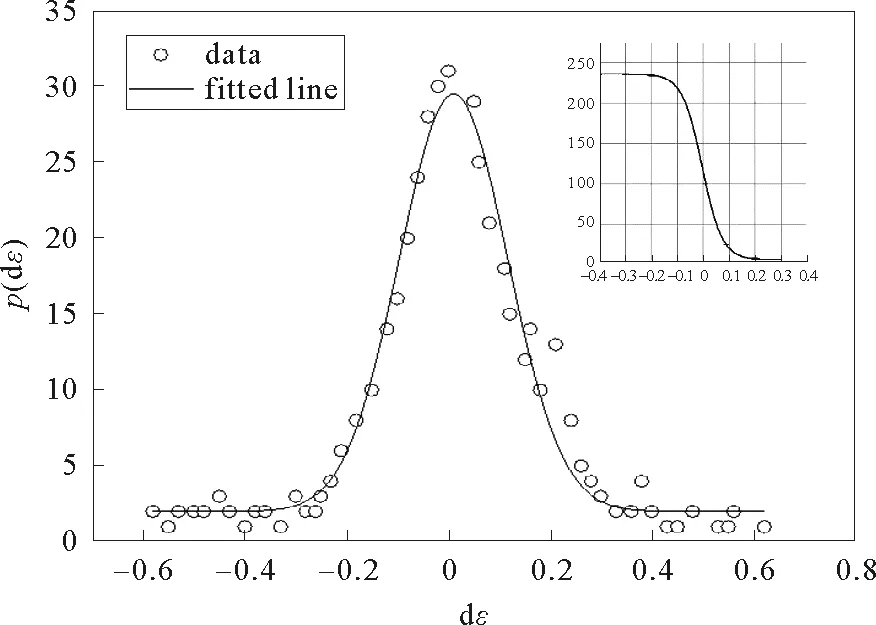
图6 全部4年增量的分布Fig.6 Distribution of full 4 years increments
(17)
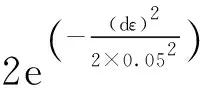
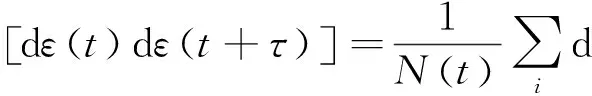
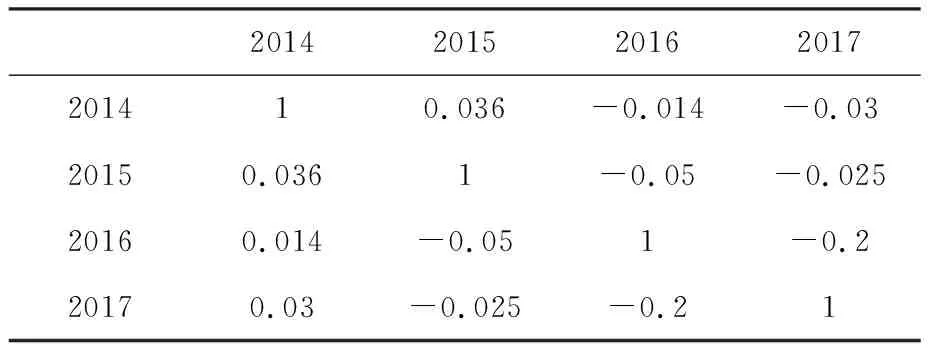
表2 自相关函数Tab.2 Autocorrelation function
由于相关性较弱,dεt可以看成是白噪声,表达式为dεt=0.05dω,并可以写为
dki=λi-0.028kidt+0.05kidω
(18)
式(18)表示了我们的模型生成的双段幂律分布的准确形式。为进一步说明模型与中国汽车制造业供应链网络演化的契合程度,根据式(18)模拟仿真了度分布。从而得到:
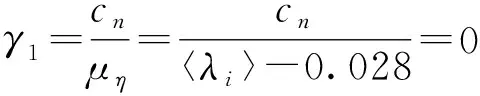
以上计算结果与模型中第一段幂指数0.47相当,而且得到的γ2的数值3.4与模型中的第二段幂指数也非常接近,从而证实了本文提出的演化算法模型的有效性。
4.3 结论
为了探寻复杂网络供应链在演化中的特性和规律,本文先是对复杂网络供应链呈现的双段幂律性和供应链演化算法的步骤进行了分析,然后结合适应度和噪声涨落因素对网络演化算法进行了完善,并利用仿真对复杂网络的演化进行了剖析,最后以汽车制造行业供应链网络为研究对象,验证了提出的网络演化模型的有效性。
通过仿真研究可以得出,服从正态分布的适应度耦合了以指数规律增长的变量,这也是双段幂律分布产生的原因;而噪声涨落并不能从根本上改变结果,但是可以影响幂指数。而在实例研究中得出,中国汽车制造业供应链网络符合模型中的演化模式,汽车制造业的净利润和净资产收益率是影响网络自组织演化过程的主导因素,噪声涨落同样存在,但是影响力很小;汽车制造业双段幂律分布的幂指数γ1和γ2分别为0.59、3.4,将这个参数控制在一个合理的范围内,供应链网络可以在有序的状态进行演化。

