变形训练在高中数学中的灵活运用

刘加韦

（山东省寿光现代中学2016级（38）班,山东 寿光）

高中阶段数学知识学习难度已经有一定加大，重点是对学生知识应用能力进行考察，其中在高中数学解题中采用变形训练方式，能够显著提高高中数学解题效率。本文结合实例分析变形训练在高中数学解题中的应用。

一、变形训练在三角函数解题中的的应用

运用这种解题方法要记住三角函数的几个公式：

万能公式：

两角和差公式：

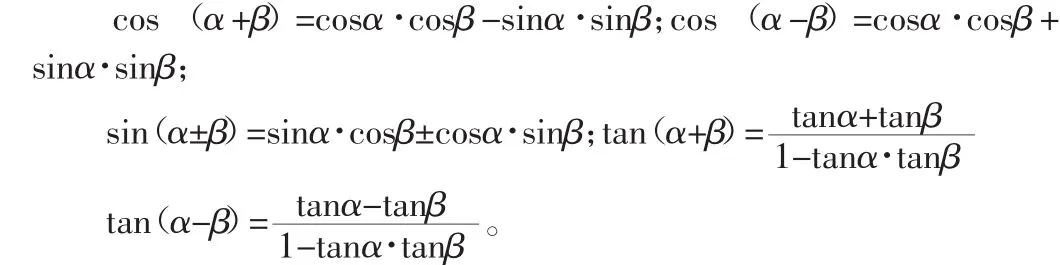
其他公式：

（sinα）2+（cosα）2=1；1+（tanα）2=（secα）2；1+（cotα）2=（cscα）2

……

例 1.求 cos250°+cos210°-sin80°sin40°的值。

根据和差化积公式：

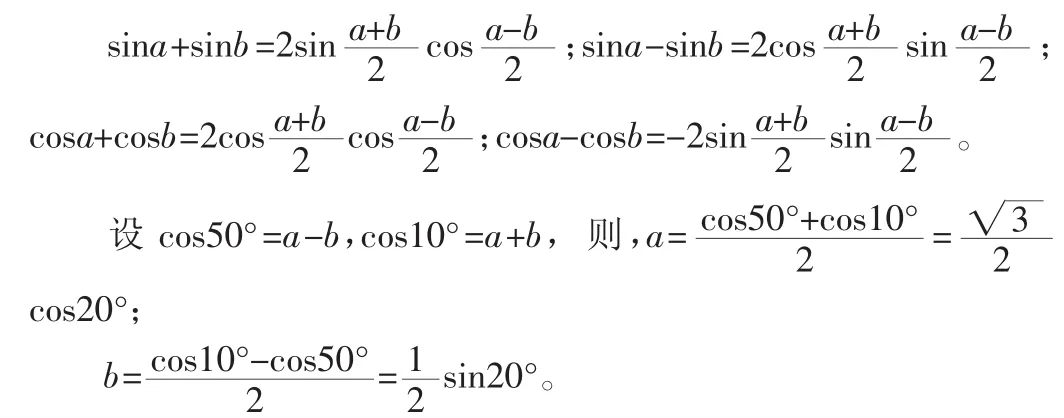
所以，原式 cos250°+cos210°-sin80°sin40°=cos250°+cos210°-cos10°

二、变形训练在基本不等式解题中的应用

高中数学中基本不等式经常用来求函数的最大值、最小值和值域等。学生遇到这样的题应当根据题目中的已知条件对式子进行灵活变形，寻找基本不等式中隐藏的定值（和或者积）作为解决问题的切入口。关于基本不等式的变形有几个基本的解题思路。

（一）常值代入

高中数学中经常需要用到常值代入到问题中，起到化繁为简的作用。经常用到的常值为：0、1、-1等。

例 2.已知 m、n∈R+，并且有那么m+n的最小值为多少？

分析：根据题目中的已知条件，将常数“1”代入到需要求解的问题中，将问题变形为含有基本不等式结构的式子，然后利用基本不等式求最小值。

另外，改善燃烧炉的操作条件也能控制燃烧炉内有机硫的生成。无论从热力学还是动力学方面而言，在可能的范围内，适当提高燃烧炉温度有助于降低过程气中的有机硫含量;增加其在燃烧炉内的停留时间，也有助于反应向平衡方向移动。

（二）拆分、增加和拼凑

解决和不等式有关的问题时可以根据已知条件对式子进行适当的拆分和拼凑，拆包括拆常数、拆系数或拆项，增添则是在不等式两边添上倍数或添上代数式。通过添加拼凑等变形方法，在基本不等式中分离出一个常值，将复杂的问题简单化。

分析：单从已知条件给出的分式来看这道题是非常难解的。但是对给出的函数进行变形就可以创造出基本不等式。

根据（x-2）2=x2-4x+4；

根据题中已知条件：x≥2.5，则f（x）≥1.5。

三、变形训练在一元二次方程解题中的应用

对于部分含有或者可以转化为一元二次方程的代数题，可以根据题目给出的式子进行适当变形，并结合代换法，可以让问题变得更加简单。

例4.已知a、b是一元二次方程x2+2000x+7=0的两个根，那么，（a2+1999a+6）（b2+2001b+8）的值是多少。

分析：根据题中条件，设：a2+2000a+7=0，b2+2000b+7=0，a+b=-2000，ab=7，

则 （a2+1999a+6）（b2+2001b+8）=（a2+2000a+7-a-1）（b2+2001b+7+b+1）

=-（a+1）（b+1）

=-ab-（a+b）-1

=-7-1+2000

=1992

变形法体现的是对公式的灵活运用，根据不同题目有时是顺向运用，有时是逆向运用，同时变形法结合配元、换元，可以灵活运用在一元二次方程、不等式和三角函数中，解决最值、值域、证明和求解问题。

指导教师评语：

该同学能够将变形法结合高中阶段数学内容进行灵活应用，由此可见该同学对高中数学的学习积累了自己的学习方法与思维模式，显著提高高中数学解题效率，成绩优秀值得学习。