网络RTK对流层延迟内插模型精度分析
李 滢,陈明剑,左 宗,姚 翔
(1. 信息工程大学导航与空天目标工程学院,河南 郑州 450001; 2. 河南省北斗导航应用技术协同创新中心,河南 郑州 450001)
地基增强系统作为一种能够提升卫星导航系统服务性能的基础性设施,在我国各省市陆续建立起来[1-2]。其能够为区域范围内用户提供高精度实时位置服务,在交通运输、智慧城市、精密农业等诸多领域具有广阔的应用前景。网络RTK技术是地基增强系统为用户提供高精度位置服务的技术保障。在网络RTK技术中,高精度的误差模型是用户进行快速、可靠定位的关键[3]。目前,对于网络RTK内插模型的研究已经较为成熟,一些研究者对现有内插模型的内插精度和适用性进行了研究,但这些分析中针对电离层延迟分析较多,对于对流层延迟的分析较少且多基于简单地形环境(站间高差小)[4-10]。相关研究表明,对流层延迟在平面和高程上存在不同的影响特性[11-12]。本文基于此进一步研究常用内插模型在复杂地形环境下(站间高差大)对流动站对流层延迟改正的精度和适用性,对网络RTK定位性能的改善具有参考意义。
河南省地基增强系统于2015年10月顺利建成,包含63个参考站完成对河南省地区的全覆盖,站点平均距离为61 km。其参考站网络的空间分布表现为:西高东低,中、东部为平原地区,地势平坦,北、西、南三面环山地形变化复杂。系统参考站网可长期连续提供BDS、GPS、GLONASS三系统多频观测数据,为网络RTK关键技术的研究提供了大量的原始数据。本文选择河南省地基增强系统北部高程差异较大的7个参考站构成试验网络,利用参考站提供的GPS观测数据,比较分析线性内插模型(linear interpolation model,LIM)、线性组合模型(linear combination model,LCM)、低趋势面模型(low-order surface model,LSM)和克里金插值法(kriging interpolation method,KRG)4种内插模型对不同高差水平流动站对流层延迟的改正效果,探究流动站对流层延迟改正的最优内插模型。
1 内插模型
常用的网络RTK内插模型包括线性内插模型、线性组合模型、低趋势面模型和克里金插值法[13-14]。网络RTK内插模型都是基于空间相关性原理,可通过数学推导建立其统一模型[4]
Vu,n=α·V=α1V1,n+α2V2,n+…+αn-1Vn-1,n
(1)
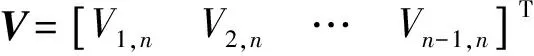
1.1 LSM和LIM
LSM模型通过简单的曲面模型来拟合区域空间相关误差,其拟合函数不唯一,本文使用的是一阶线性拟合函数
V=a·ΔX+b·ΔY+c
(2)
(3)
其中

LIM模型与LSM模型类似,其拟合函数更为简单
V=a·ΔX+b·ΔY
(4)
需要至少3个参考站,通过最小二乘计算LIM的内插系数向量
(5)
式中
1.2 LCM
LCM模型通过构建单差线性组合观测值对空间相关误差建模,内插系数向量满足以下约束条件[15]
(6)
至少需要3个参考站,可计算得到LCM内插系数向量
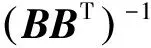
(7)
式中
1.3 KRG
KRG模型是一种空间自协方差最佳差值方法,考虑了样本数据在空间和时间上的相互关系[16],其内插系数向量为[5]
(8)
其中
式中,cij为lij参考站i和j之间的协方差函数,本文中选择距离线性函数cij=lmax-lij。其中lij为参考站i和j之间的距离,lmax为最大距离,需大于参考站间最长距离。
2 试验分析
为比较分析4种常用网络RTK内插模型对不同高差水平流动站对流层延迟的改正效果并探究流动站对流层延迟改正的最优模型,选取河南省地基增强系统参考站网的7个参考站构成试验网络,各站点站名缩写及其所对应中文全称见表1(mref、ref、rov分别表示主参考站、参考站和流动站),其中WWSZ站为主参考站,SMJZ、SXJZ、DFJZ为辅参考站,选择与主参考站高差较小的MCJZ站,以及与主参考站高差达到近400 m的LMJZ、BAJZ站为流动站且BAJZ站位于网外。试验数据选取7个站点2017年4月4日近30 min的观测数据,采样间隔为1 s。试验网络平面分布和各站点高程信息分别如图1和表2所示。

表1 试验网络站点名称

图1 试验网络平面分布
观测时段内参考卫星为G05,为探究卫星高度角对模型内插精度的影响,选择观测时段内高度角较高的卫星G02和高度角较低的卫星G06为试验卫星。将天顶对流层延迟作为待估参数与双差整周模糊度一并求解,在固定整周模糊度之后可准确计算出基线上的双差对流层延迟。利用自研GAUSS软件计算出6条独立基线(WWSZ—SMJZ、WWSZ—SXJZ、WWSZ—DFJZ、WWSZ—MCJZ、WWSZ—LMJZ、WWSZ—BAJZ)上每个历元的双差对流层延迟作为真值。根据流动站与参考站之间的位置关系由式(5)、式(7)、式(3)和式(8)分别计算出LIM、LCM、LSM及KRG 4种内插模型的内插系数,利用解算出的WWSZ—SMJZ、WWSZ—SXJZ、WWSZ—DFJZ基线上的双差对流层延迟,内插出各流动站与主参考站间的双差对流层延迟并与计算的双差对流层延迟真值进行比较。

表2 试验网络高程信息 m
图2为试验网络各基线上双差对流层延迟的变化情况。从图中可以看出WWSZ—DFJZ及WWSZ—SXJZ基线上的双差对流层延迟较大,WWSZ—MCJZ基线上的双差对流层延迟最小。对比图2(a)和图2(b)可以看出,双差对流层延迟与卫星高度角呈反相关,高高度角卫星G06各基线上的双差对流层延迟相较于低高度角卫星G02各基线上的双差对流层延迟整体上有所增大,最大增加可达约2 dm。
为比较4种内插模型在流动站MCJZ(高差较小、网内)的内插效果,给出其双差对流层延迟内插值与真实值的比较,如图3和图4所示。图中,横坐标表示历元,历元间隔为1 s,左边纵坐标为双差对流层延迟,右边纵坐标为卫星高度角。虚线表示卫星高度角,在观测时段内G02在67.8°~68.4°范围内变化,G06由36.7°下降到29.1°。从图3中可以看出,在卫星高度角较高情况下,MCJZ 4种内插模型内插值与真值都偏差较小,其中LSM内插效果较差。图4相比于图3,MCJZ 4种内插方法内插值和真值的偏差都有所增大,这是因为在观测时段内G06卫星高度角较低,参考站间双差对流层延迟增大,影响模型内插精度。总体来看,对于与主参考站高差较小且位于网内的流动站MCJZ,4种内插模型的内插精度相差不大,整体精度较高,满足网络RTK用户高精度定位需求。
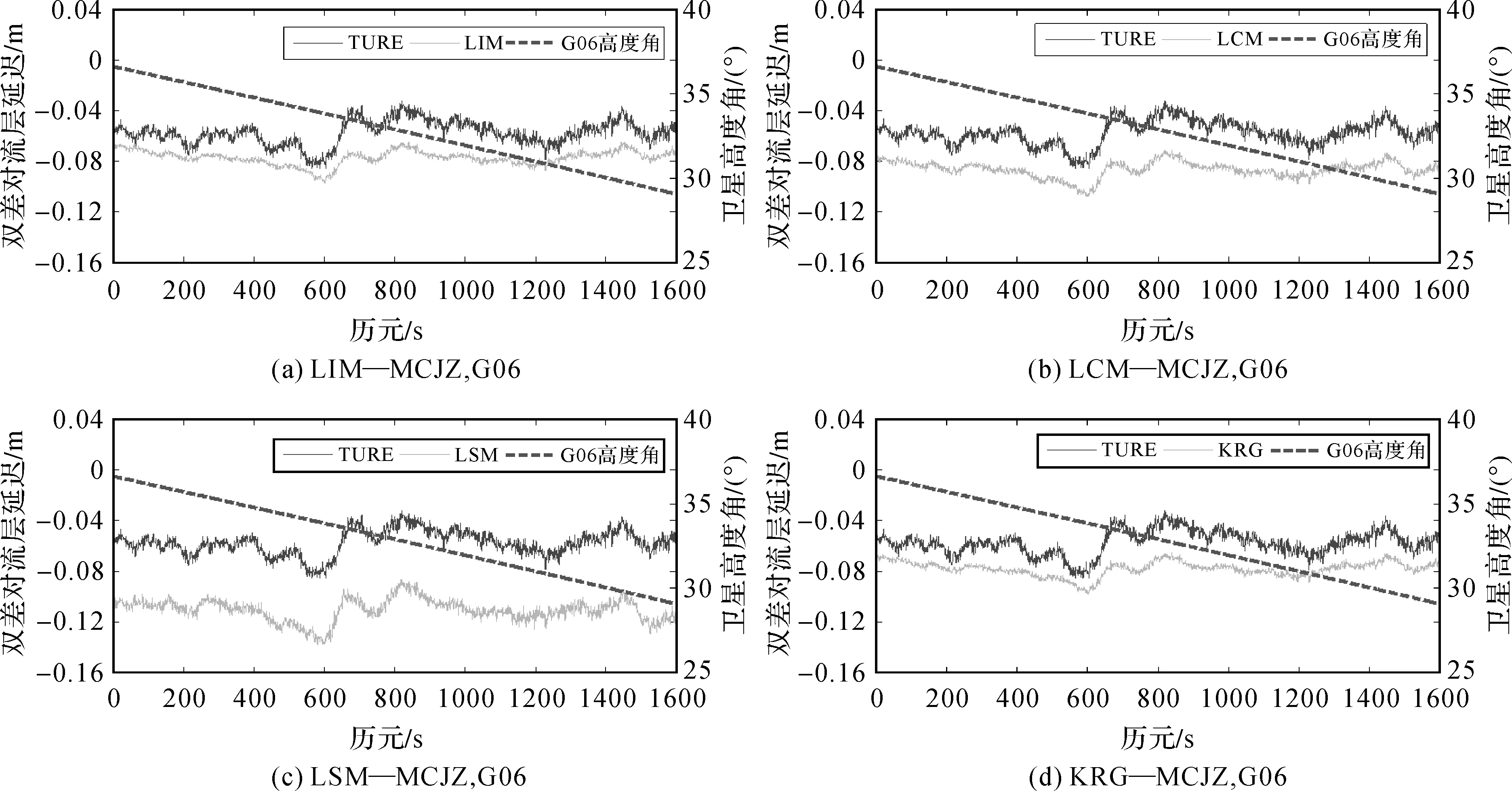
图4 MCJZ双差对流层延迟内插值与真实值的比较(G06)
为进一步探究规律的一般性,下面通过统计各流动站4种内插模型内插值与真实值偏差的最大值(绝对值)、平均值和中误差,分析4种内插模型对不同流动站(站间高差差异、平面位置差异)对流层延迟改正的精度。3个流动站卫星G02和G06的内插精度统计分别见表3和表4,图5绘制了各流动站的内插中误差。
由表3、表4及图5可以得出:
(1) 4种内插模型中,LSM模型内插精度较差,LIM模型内插精度较优,KRG模型网内内插精度与LIM模型相当,网外内插精度有所降低。
(2) 对于与主参考站高差较小的流动站MCJZ,LSM模型内插精度可达5 cm,其他3种内插模型的对流层延迟内插精度在3 cm以内,且精度相差不大。即流动站与主参考站站间高差较小时,4种内插模型精度较高,基本满足网络RTK大气改正的需求。
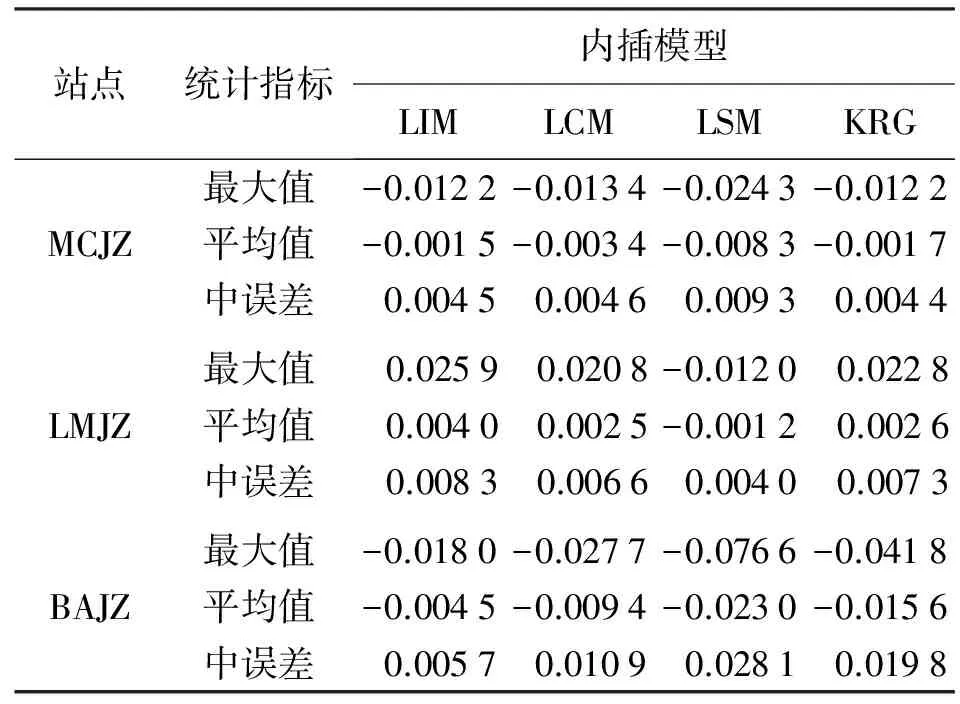
表3 各流动站4种内插模型改正精度统计(G02) m
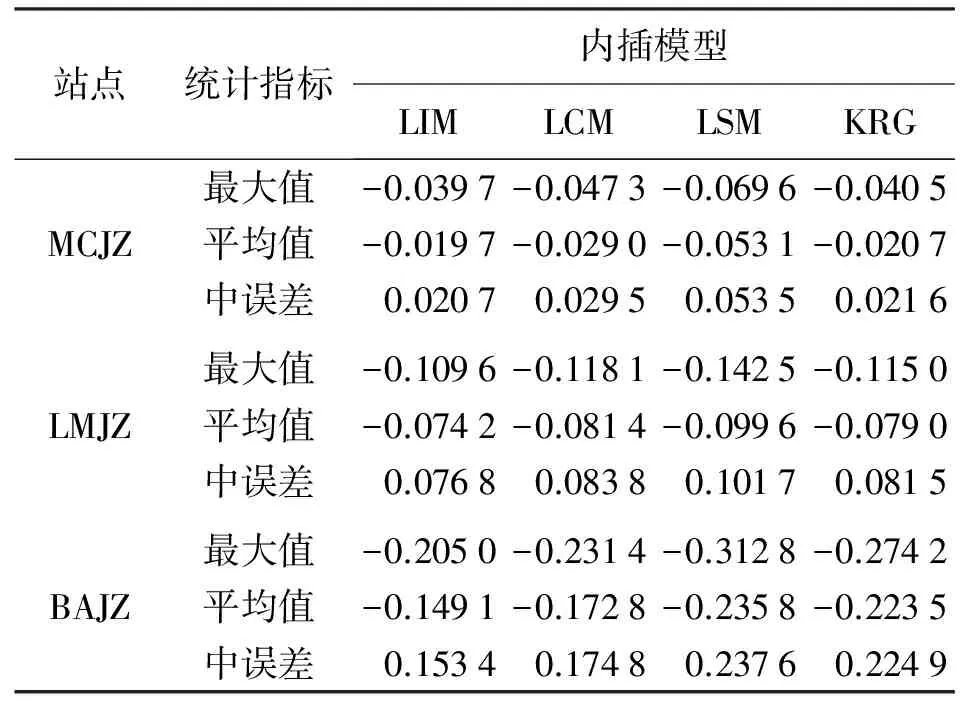
表4 各流动站4种内插模型改正精度统计(G06) m
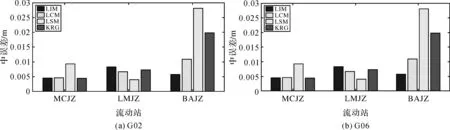
图5 各流动站内插中误差
(3) 对于与主参考站高差约为400 m的流动站LMJZ和BAJZ,4种内插模型的对流层延迟改正精度均有所降低,且网外较网内内插精度下降幅度大。模型内插精度随卫星高度角的降低而下降,对于高高度角卫星(本文约60°),4种内插模型无论网内还是网外对流层延迟改正精度都下降不大;对于低高度角卫星(本文约30°),4种内插模型精度降低到分米级,不满足网络RTK大气改正需求。
3 结 语
本文采用河南省地基增强系统参考站网数据,比较LIM、LCM、LSM、KRG 4种内插模型对流动站对流层延迟改正的效果。本文试验说明LIM模型和KRG内插精度较优,是流动站对流层延迟改正的优选内插模型。流动站与主参考站站间高差较小时,4种内插模型精度较高,基本满足网络RTK大气改正的需求。当流动站与主参考站高差达到400 m时,低高度角卫星情况下4种内插模型精度降低到分米级,特别对于网外用户,4种内插模型的改正精度不满足网络RTK用户高精度定位的需求。因此,现有常用内插方法不适用于高差较大区域流动站对流层延迟的改正,需对常用内插模型改进和精化。可以在选择较优内插模型的基础上对站间高差引起的模型误差进行修正,以提高流动站对流层延迟的改正精度。随着地基增强系统的不断完善和北斗应用的逐步推广,基于BDS的网络RTK对流层延迟内插方法将是下一步研究的重点。
[1] 陈伏州.关于我国北斗地基增强系统发展的思考[J].数字通信世界,2013(8):24-27.
[2] 尹子明,刘天恒,张树为,等.BDS地基增强系统单双模定位性能比较[J].导航定位学报,2016,4(3):64-68.
[3] 吴北平.GPS网络RTK定位原理与数学模型研究[D].武汉:中国地质大学,2003.
[4] DAI L,HAN S,WANG J,et al.Comparison of Interpolation Algorithms in Network-based GPS Techniques[J].Navigation,2003,50(4):277-293.
[5] 张绍成.基于GPS/GLONASS集成的CORS网络大气建模与RTK算法实现[D].武汉:武汉大学,2010.
[6] SHAERY A M,LIM S,RIZOS C.Investigation of Different Interpolation Models Used in Network-RTK for the Virtual Reference Station Technique[J].Journal of Global Positioning Systems,2011,10(2):136-148.
[7] 冯彦同,刘晖,张海平,等.网络RTK综合误差内插算法的比较与分析[J].测绘地理信息,2013,38(1):20-22.
[8] TANG W.GNSS Network RTK Regional Ionospheric Modelling Studies and Performance Analysis[J].Journal of Navigation,2016,69(1):211-224.
[9] 邓健,赵兴旺,张爱国.长距离稀疏参考站下网络RTK电离层误差内插模型精度分析[J].测绘科学技术学报,2015,32(3):236-240.
[10] 邱蕾,罗和平,王泽民.GPS网络RTK流动站的对流层内插改正分析[J].测绘工程,2011,20(5):70-73.
[11] 张锋,郝金明,丛佃伟,等.基于多参考站网络的VRS算法研究与实现[J].测绘科学技术学报,2008,25(6):414-416.
[12] 谢建涛.VRS改正数算法研究及精度分析[D].郑州:解放军信息工程大学,2013.
[13] 李成钢,黄丁发,袁林果,等.GPS参考站网络的电离层延迟建模技术[J].西南交通大学学报,2005,40(5):610-615.
[14] SHAERY A M,LIM S,RIZOS C.Functional Models of Ordinary Kriging for Medium Range Real-time Kinematic Positioning Based on the Virtual Reference Station Technique[C]∥ION GNSS.Portland:[s.n.],2010.
[15] 黄丁发,周乐韬,李成钢,等.GPS增强参考站网络理论[M].北京:科学出版社,2011.
[16] 郭秋英,郝光荣,陈晓岩.中长距离网络RTK大气延迟的Kriging插值方法研究[J].武汉大学学报(信息科学版),2012,37(12):1425-1428.

