波浪作用下椭圆形横截面悬浮隧道管段压强特性试验
李勤熙, 蒋树屏, 丁 浩, 李 科
0 引言
近年来,我国水下隧道建设所处的水域环境和地质条件越来越复杂,水深越来越大,距离越来越长,传统建设工法在复杂水域面临着巨大的挑战,需要不断突破和创新。 “钻爆法+盾构法”、“沉管法+悬浮法”和“盾构法+沉管法”等组合工法已成为工程建设的备选项。悬浮隧道作为一种跨越深水水域的全新水下隧道概念结构已引起世界各国的关注,国内相关研究至今也已有20多年,在悬浮隧道结构计算理论、模型试验、设计指南及施工方法等方面取得了一系列成果,围绕小比尺模型试验和精细化理论形成了基础理论成果,在千岛湖、琼州海峡和台湾海峡等水域也尝试过工程应用层面的前期研究。
事实上,真正的悬浮隧道实践起来困难重重,迄今为止,世界上仍没有一例真正建成的悬浮隧道。F.M.Mazzolani等[1]针对中国的千岛湖悬浮隧道开展了设计研究,列举出建设全尺寸悬浮隧道时建设位置的选取、结构方案和不同设计阶段的设计要求、设计工作和设计成果等一系列问题; R.M.Larssen等[2]针对挪威建设峡湾海中悬浮隧道工程建设时提出的张力腿式、浮筒式和柱式等多种模型进行了研究,推荐采用浮筒式悬浮隧道跨越; F. Perotti等[3]从悬浮隧道和悬索桥均为柔性结构体系的共同点出发,回顾了悬浮隧道动力特性的研究成果,首次总结了悬浮隧道在低频动力响应、冲击荷载作用以及隧道内部和外部爆炸荷载作用下的一般性原则,讨论了流-固耦合作用时发生涡激响应的危险时间。从20世纪90年代开始,日本对喷火湾[4]、大阪湾等跨海通道工程的水中悬浮隧道方案进行了重点研究,Shunji Kanie[5]总结了日本近20年在悬浮隧道领域的相关研究,并针对日本多处拟建跨海通道的海峡进行了模型分析。目前,国内在部分地区虽有相关工程前期立项策划,但在悬浮隧道领域尚处于起步阶段,且主要集中于基础理论方面的研究[6-11]。总体而言,国内外学者的基本共识是在一定深度下波浪力的影响很小,可忽略不计,但这一结论的前提是在表面波作用下。自然界中存在着表面波,还有海洋内波,根据麦继婷等[12]和Hiroshi Kunisu[13]的研究,虽然海洋内波随着埋深的增加量值会减小,但减小的幅度却越来越小,在超过100 m的水深后仍有较大的波浪力。对工程而言,一方面,如果在实践时采用纯悬浮隧道方案,那么必然存在进口段、过渡段和深埋段,无论是表面波还是海洋内波的波浪力都会对进口段和过渡段产生影响; 另一方面,如果采用组合式工法,就必然存在接驳问题,那么就必须衡量波浪力的大小以确定最佳接驳位置。因此,从技术上和工程上来看,波浪力值得研究。
由于数值模拟和试验条件的局限性,目前关于波浪力的物理模型试验并不多。Hiroshi Kunisu等[14]通过物理模型试验设计了一种跨越北海道Funka湾的SFT结构,在一个二维波浪水槽中产生规则波浪,通过改变试验水深、波浪要素进行了工况组合试验; S.H. Oh等[15]也通过波浪水槽中的规则波物理试验研究了SFT在波浪作用下的水动力特性,不同的是其首次在试验测试中应用了结构运动图像识别技术; 王广地[16]虽然研究了波流作用下悬浮隧道的结构响应,但限于试验条件,其研究主要集中在水流作用下的结构响应,并没有考虑波浪。本文以琼州海峡跨海通道为试验背景,设计了一种椭圆形双向6车道公路交通悬浮隧道,研究了椭圆形断面悬浮隧道在波浪作用下的结构波动特性,以期为新结构形式悬浮隧道的继续优化和开发提供思路。
1 波浪水槽试验
1.1 相似准则
悬浮管段在水中主要受波浪力、洋流力和地震等荷载的作用。根据Mirosion方程计算的波浪力主要包括惯性力和阻尼力。对于动力试验,应满足Froude相似和雷诺相似,事实上,同时满足这2者相当困难。参考船舶流体力学试验和传统水动力学试验,根据波浪要素、设计水位、试验断面和试验设备,并考虑水力试验的尺寸效应和试验场地的现实条件,综合确定模型试验比尺为1∶60,采用正态模型。模型试验管段、锚索和波浪应满足以下准则。
1.1.1 管段相似
管段相似应根据几何相似、质量相似进行设计。参考大量的船舶流体力学试验和传统水动力学试验,管段材料选用有机玻璃,以便对试验过程进行观察; 管段质量相似主要是利用浮重比进行控制,本试验的浮重比设计为1.3。本试验是水槽中的管段断面试验,因此认为管段的刚度足够大,暂不考虑流体和管段结构的刚度比,但在开展水池平面试验时需考虑。长度比尺、时间比尺、压强比尺计算公式分别为

(1)
Tr=λ1/2;
(2)
Pr=λ。
(3)
式中:L、B、H分别代表坐标系中长、宽、高的3个方向;Lp、Bp、Hp为实际长度;Lm、Bm、Hm为模型长度;λ为模型比尺,λ=60;Tr为时间;Pr为压强。
1.1.2 锚索模拟
锚索属于非刚性结构,按受力变形相似和质量相似进行模拟。锚索模型应与原型的拉力-伸长关系曲线相似,根据JTJ/T 234—2001《波浪模型试验规程》,确定模型锚索拉力-伸长关系为
(4)
式中:Tm为模型锚索拉力,N;CP为原型锚索弹性系数,对于钢缆CP=26.97×104MPa;dp为原型锚索直径,m; ΔS/S为原型锚索相对伸长,S为原型锚索初始长度;n为指数,对于钢缆可取1.5。
根据JTJ/T 234—2001《波浪模型试验规程》,缆绳的质量相似按式(5)进行计算:
(5)

1.1.3 波浪相似
波浪模拟满足重力相似条件,不规则波谱采用JONSWAP谱,其表达式为:

(6)
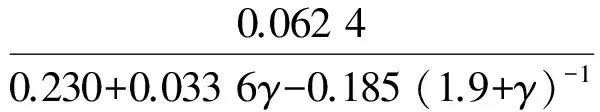
fp为谱峰频率;Hs为有效波高,m;Tp为谱峰值周期,s;γ为谱峰值参数,取γ=3.3。
1.2 试验方法
本文按照双向6车道设计了一种椭圆形断面悬浮隧道交通结构,断面的长轴和短轴尺寸分别为45.0 m和19.0 m,如图1所示。目前,世界上尚未见已建成悬浮隧道工程的报道。本文以琼州海峡为工程背景,采用琼州海峡的水文地质参数进行研究,琼州海峡全年中浪(波高1.25~2.5 m)和大浪(波高2.5~4 m)占波浪的80%左右[17]。为了得到可靠的波浪要素,首先对波浪进行了滤波处理,反复试验后得到了满足要求的波浪要素程序。试验时在计算机中对需要的波浪要素程序进行调用,选取了3组波高、3组周期共9组工况进行试验,悬浮隧道工况设计见表1。悬浮隧道支撑形式为锚索式,锚索角度设置为45°,试验时在静水中造波,波浪设置为规则波,并按波浪运动方向垂直于隧道走向的平面模型开展试验,试验方案设计如图2所示。

图1 椭圆形结构断面(单位: mm)

断面形式车道数实际断面尺寸/(m×m)实际波高/m实际波浪周期/s试验断面尺寸/(m×m)试验波高/cm试验波浪周期/s试验水深/cm椭圆形641.1×13.61.211.622.413.943.616.270.685×0.22721.541.862.110
1.3 试验设备
试验选用中星测控公司生产的压力测量系统和总力测量系统,传感器的原理均是由模拟量转化为数字量,不同的是压强传感器由应变转化而来,而压力传感器靠形变量转化。压力测试系统和总力测试系统的主要测试参数见表2。
为了测试水下悬浮隧道的周向压强,在隧道表面设计了8个均匀分布的测点,布置在断面的关键位置,如图3所示。试验波浪水槽的尺寸为60 m×1 m×1.8 m(长×宽×高),悬浮隧道试验管段长度据此确定为85 cm,现场测试图见图4。

图2 试验方案设计图(单位: m)

类型传感器量程分辨精度/%采样频率/Hz压力测量系统10~20kPa10.008总力测量系统2~30kg10.03

(a) 锚索测点

(b) 压强测点
P1—P6、P8、P9均为断面测点。因原测点P7破坏,故采用P9代替。
图3关键位置测点布置
Fig. 3 Layout of key monitoring positions
1.4 试验消浪
本试验为水槽试验,水槽被分为2部分,下半部分为试验区域,平面布置图如图5所示。试验时,当波浪传播至试验区域遇到结构后会发生反射,反射波一部分在上方的平行水槽中扩散,传至尽头的碎石处被破碎,能量耗散; 另一部分则会反射回导流板附近,通过波高仪可以测得反射波的波高,利用计算机控制的导流板对其进行消波处理。因此,无论是传播经过试验区域的波浪还是从试验区域前部反射回去的波浪均得到很好的消浪处理,不会造成波浪的叠加。试验时,每一组工况的间隔时间应足够长,待水流稳定后再开展下一组试验,以防止波浪的反复叠加。

(a) 俯视图

(b) 侧视图

图5 水槽平面布置图
2 主要试验结果分析
由于波浪运动方向的差异,波浪力会在悬浮隧道断面的不同位置形成不同的压强场分布,包括背浪面、迎浪面、上表面和下表面。由于同一位置不同时刻压强的变化和不同位置同一时刻压强差的存在,使得悬浮隧道存在明显的波动特性。
因此,选取悬浮隧道结构的1号(迎浪面)、3号(下表面)、5号(背浪面)、9号(上表面)4个传感器的数据进行分析,其中1号和5号主要观测隧道迎浪面和背浪面的压强变化情况。对1号和5号、3号和9号传感器数据做差之后可以得到隧道迎、背浪面和上、下表面的压强差值,据此可以分析隧道的稳定性和安全性。
为消除测试设备的仪器误差,引入相对压强幅值
DP=Pi-P0。
(7)
式中:Pi为i时刻的压强;P0为初始时刻的压强。
2.1 压强包络线
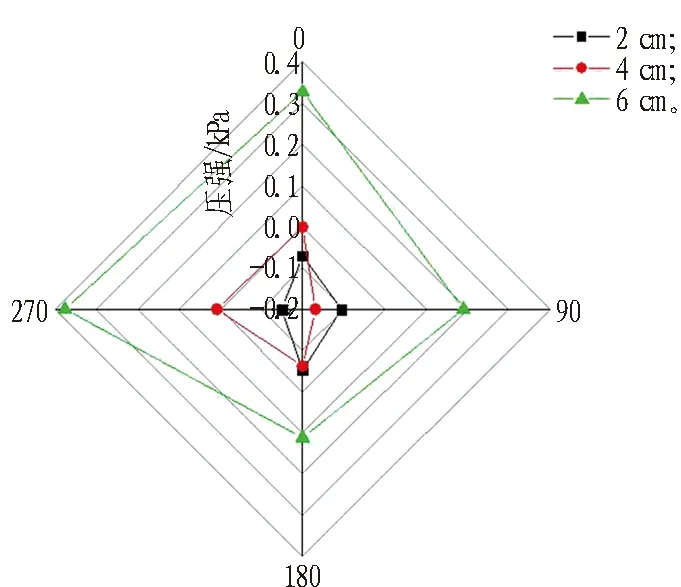
为分析悬浮隧道结构的周向压强典型变化特性,取波高6 cm、波浪周期为1.5~2.1 s以及周期为2.1 s、波高为2~6 cm时的工况,得到悬浮隧道4个关键测点在不同周期和波高下的压强值。图6和图7分别示出波高6 cm不同周期下和周期2.1 s不同波高下的悬浮隧道压强包络图。为使试验结果可靠,从足够长的时刻(t=60 s)开始取测点压强。
试验分别测试了2~6 cm波高和1.5~2.1 s周期的工况,现以6 cm波高和2.1 s周期为例进行分析。在6 cm波高工况下,迎浪面达到波峰时压强绝对值随周期的增大而减小,迎浪面达到波谷时压强绝对值也随周期的增大而减小; 在2.1 s周期工况下,迎浪面达到波峰时压强绝对值随波高增大而增大,迎浪面达到波谷时压强绝对值也随波高的增大而增大。迎浪面的波峰波谷时刻各方向的压强相差较大,压强在椭圆形表面分布不均匀。表3给出了所有试验工况下的上下表面压强差与迎背浪面压强差之比。虽然不同的工况下压强差之比具有随机性,但总体而言,上下表面的压强差大于迎背浪面压强差。从波峰时刻来看,上下表面压强差与前后表面压强差的比值平均为1.88,波谷时刻上下表面压强差与前后表面压强差的比值平均为2.08,说明椭圆形悬浮隧道垂向稳定性没有水平向稳定性好,应予以重点关注。
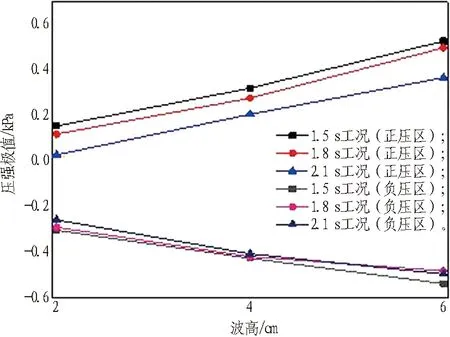
2.2 压强极值
当波高在2~6 cm变化时,使波浪周期在1.5~2.1 s变化,得到悬浮隧道各测点在不同波浪周期下的压强值。图8示出迎浪面、背浪面压强极值随波高的变化曲线。由图8可以看出,在相同周期下,迎浪面、背浪面压强极值和上下表面压强差极值在正压区随波高的增大而增大,在负压区压强极值、压强差极值的绝对值也随之增大,各测点正负压强极值的绝对值表现为6 cm波高工况>4 cm波高工况>2 cm波高工况,其极值增大率平均值分别为48.5%和41.1%; 在相同波高下,压强极值随周期的增大而规律性减小,各测点正负压强极值的绝对值表现为1.5 s周期工况>1.8 s周期工况>2.1 s周期工况,其极值增大率的平均值分别为9.7%和8.8%。因此,可以看出周期对压强极值的影响极为有限,周期对压强极值的敏感性不如波高,说明波高对悬浮隧道的水动力响应强于波浪周期。

(b) 迎浪面达到波谷时刻
Fig. 6 Comparison of pressure envelope diagrams under different wave periods when wave height is 6 cm
(a) 迎浪面达到波峰时刻

(b) 迎浪面达到波谷时刻
Fig. 7 Comparison of pressure envelope diagrams under different wave heights when wave period is 2.1 s
表3上下表面压强差与前后表面压强差之比
Table 3 Ratio of pressure difference between upper and lower surface to that between front and back surface

周期工况/s波峰时刻压强差比波高2cm波高4cm波高6cm波谷时刻压强差比波高2cm波高4cm波高6cm1.52.181.781.462.332.441.371.82.032.411.262.161.981.592.13.001.521.242.713.121.06

(a) 迎浪面
(b) 背浪面

(c) 上下表面压强差
Fig. 8 Pressure peak variation with wave height under different wave periods
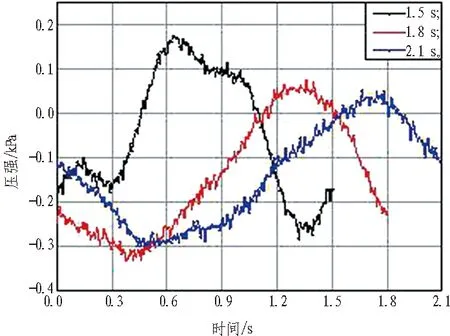
2.3 压强峰值次数
在一个波浪周期内,悬浮隧道结构出现了多个局部峰值,为讨论其峰值次数变化规律,现以2 cm波高工况为例,在1.5~2.1 s内变化波浪周期,得到悬浮隧道迎浪面、背浪面、迎背浪面压强差和上下表面压强差在不同波浪周期下的压强值,如图9所示。图10示出2、4、6 cm波高下不同周期的迎背浪面压强出现峰值次数的比较。由图10可知,迎背浪面压强出现峰值次数的规律表现为: 2.1 s周期工况>1.8 s周期工况>1.5 s周期工况。

(a) 迎浪面
(b) 背浪面

(c) 迎背浪面压强差
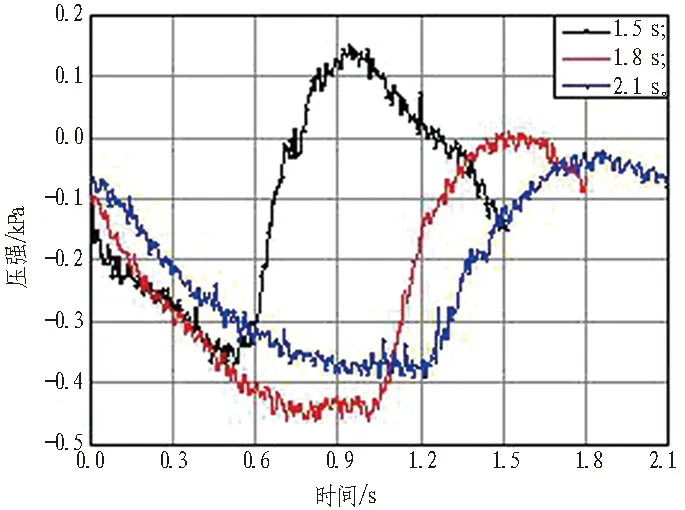
(d) 上下表面压强差
Fig. 9 Pressure variation with wave period when wave height is 2 cm

(a) 波高2 cm

(b) 波高4 cm

(c) 波高6 cm
Fig. 10 Comparison of peak times of wave face and wave back face under different wave periods
由图8可知,无论是从正压区还是负压区来看,短周期波浪的压强绝对值总是大于长周期波浪。由图9可知,对于长周期波浪,波浪力产生的压强接近正弦变化; 对于短周期波浪,压强响应不再是协调的,但仍然保持一定的周期变化,波浪力变化趋于复杂。而图8又表明,短周期波浪相比长周期波浪强度更大,变化更复杂。由图10可知,长周期波浪周期内出现的峰值次数最多,绝对量值没有短周期波浪大。因此,短周期波浪对隧道稳定性影响更为显著。
3 结论与讨论
1)从瞬时时刻的悬浮隧道结构压强包络线来看,压强随波高的增大而增大,随周期的增大而减小。悬浮隧道结构的垂向稳定性低于水平向,在结构设计和施工过程中应重点关注。
2)周期变化对压强极值的影响小于波高变化对压强极值的影响,波高是结构所受压强绝对值的主要影响因素之一。
3)短周期波浪的破坏力要大于长周期波浪,表现为峰值大、影响快,而长周期波浪虽然影响时间略长,但峰值不大。在不同的波高下,峰值出现次数的规律为2.1 s周期工况>1.8 s周期工况>1.5 s周期工况。
4)限于试验条件,本试验仅测试分析了悬浮隧道管段的压强变化特性,未来应在管段压强测试的基础上进一步测定结构的应力分布和不同锚索布置形式的受力特性,并对结构安全性进行试评价。
[1] MAZZOLANI F M, FAGGIANO B, MARTIRE G. Design aspects of the AB prototype in the Qiandao Lake[J]. Procedia Engineering, 2010, 4: 21.
[2]LARSSEN R M, JAKOBSEN S E. Submerged floating tunnels for crossing of wide and deep fjords[J]. Procedia Engineering, 2010, 4: 171.
[3] PEROTTI F, BARBELLA G, PILATO M D. The dynamic behaviour of Archimede′s Bridges: Numerical simulation and design implications[J]. Procedia Engineering, 2010, 4: 91.
[4]KUNISU H, MIZUNO S, MIZUNO Y, et al. Study of submerged floating tunnel characteristics under the wave condition[C]// The Fourth International Offshore and Polar Engineering Conference. Osaka: International Society of Offshore and Polar Engineers, 1994.
[5] KANIE Shunji. Feasibility studies of various SFT in Japan and their technological evaluation[J]. Procedia Engineering, 2010, 4: 13.
[6] JINAG Shuping, LI Qinxi, LI Jianjun, et al. Research on risk sensitivity of submerged floating tunnel based on analytic hierarchy process [J]. Procedia Engineering, 2016, 166: 255.
[7] 麦继婷, 杨显成, 关宝树. 波流作用下悬浮隧道的动态响应分析[J]. 水动力学研究与进展, 2005, 20(5): 616.
MAI Jiting, YANG Xiancheng, GUAN Baoshu.Dynamic response analysis of the submerged floating tunnel subjected to the wave and current [J]. Journal of Hydrodynamics, 2005, 20 (5): 616.
[8] 董满生, 洪友士.辛体系下曲线形水中悬浮隧道对波浪激励的动力响应研究[J].应用力学学报, 2008, 25(4): 535.
DONG Mansheng, HONG Youshi. Study of dynamic response of curved submerged floating tunnel under wave excitation in symplectic system [J]. Chinese Journal of Applied Mechanics, 2008, 25 (4): 535.
[9] 惠磊, 葛斐, 洪友士.水中悬浮隧道在冲击载荷作用下的计算模型与数值模拟[J]. 工程力学, 2008, 25(2): 209.
HUI Lei, GE Fei, HONG Youshi.Calculation model and numerical simulation of submerged floating tunnel subjected to impact loading [J]. Engineering Mechanics, 2008, 25 (2): 209.
[10] DING Hao, LI Qinxi, JIANG Shuping, et al. Research progress and outlook on critical characteristics of submerged floating tunnels [J]. Procedia Engineering, 2016, 166: 347.
[11]LIANG Bo, JIANG Bolin. Study of composition and simulation analysis of traffic loads in submerged floating tunnels [J]. Procedia Engineering, 2016, 166: 180.
[12] 麦继婷, 关宝树. 用Morison方程计算分析悬浮隧道所受波浪力初探[J]. 石家庄铁道学院学报, 2003, 16(3): 1.
MAI Jiting, GUAN Baoshu. A preliminary calculating analysis of the wave forces on a submerged floating tunnel by applying the Morison equation[J]. Journal of Shijiazhuang Railway Institute, 2003, 16(3): 1.
[13]KUNISU Hiroshi. Evaluation of wave force acting on submerged floating tunnels[J]. Procedia Engineering, 2010, 4: 99.
[14] KUNISU Hiroshi, MIZUNO Susumu, MIZUNO Yuzo, et al. Study of submerged floating tunnel characteristics under the wave condition[C]// The Fourth International Offshore and Polar Engineering Conference. Osaka: International Society of Offshore and Polar Engineers, 1994.
[15]OH S H, PARK W S, JANG S C, et al. Physical experiments on the hydrodynamic response of submerged floating tunnel against the wave action[C]//Proceedings of the 7th International Conference on Asian and Pacific Coast. Makassar: Hasanuddin University Press, 2013.
[16] 王广地. 波流作用下悬浮隧道结构响应的数值分析及试验研究[D]. 成都: 西南交通大学, 2008.
WANG Guangdi. Numerical analysis and experimental study of structural response of submerged floating tunnel under wave current[D]. Chengdu: Southwest Jiaotong University, 2008.
[17] 耿宝磊, 文先华. 台风作用下琼州海峡海域波浪特征分析[J]. 海洋工程, 2013, 31(6): 59.
GENG Baolei, WEN Xianhua. Analysis of wave characteristics of Qiongzhou channel in typhoon period[J]. The Ocean Engineering, 2013, 31 (6): 59.

