Fe-11Mn-10Al-0.9C低密度钢的变形抗力模型和热加工图
刘德罡,胡小龙,蔡明晖,丁 桦
(东北大学 材料科学与工程学院,沈阳 110004)
随着能源危机和环境污染问题的日益严重,在保证安全性能的前提下尽可能轻量化以降低油耗和减少温室气体的排放,已成为现代汽车工业的发展趋势[1].通过向钢中加入一定量的Al元素,在获得良好强韧性的同时,凭借扩大钢的晶格常数和其低的相对原子质量降低钢的密度,可显著提高钢在汽车工业中应用的优越性和竞争力[2-3].目前,Fe-Mn-Al-C系低密度钢的研究和开发受到广泛关注.为了获得强塑性配合较好、可应用于汽车工业的低密度钢板,需要通过合理的锻造、轧制等热加工工艺环节.变形抗力作为轧制过程最基本的控制参数,其精确计算成为顺利进行轧制生产的必要条件[4].建立材料的热加工图,结合加工过程中材料的组织特征分析其不同变形条件下的高温变形机制,从而明确热加工“安全区”和“不安全区”,实现组织调控、避免缺陷产生和优化工艺参数的目的[5].
本文对中锰高铝Fe-11Mn-10Al-0.9C低密度钢进行研究,在热模拟机上进行单道次压缩实验,分析热加工工艺参数(变形程度、变形温度和应变速率)对变形抗力的影响,建立合理的变形抗力模型,为制定合理的热轧工艺规程提供技术支撑和理论指导,同时,建立热加工图,确定该材料最佳的热加工工艺窗口.
1 实验材料及研究方法
本文采用的实验材料为Fe-11Mn-10Al-0.9C低密度钢.利用真空感应炉熔炼铸造得到50 kg 钢锭,具体化学成分(质量分数/%)为:C 0.92,Mn 11.36,Al 9.86,余量为Fe.将钢锭锻造成截面尺寸为40 mm×100 mm的方形坯料,通过在1 200 ℃保温2 h的均匀化处理后得到12 mm的热轧板.在1 000 ℃保温1 h水淬处理后,在热轧板上沿轧制方向加工尺寸为Φ8 mm×15 mm的圆柱形试样.
在Gleeble-1500热模拟试验机上进行单道次压缩实验,以30 ℃/ s加热到1 250 ℃保温240 s后,以20 ℃/ s冷却到变形温度保温30 s,进行压缩变形,达到真应变0.7,立即水冷以保持高温变形组织.变形温度为800~1 100 ℃,应变速率为0.001~10 s-1.
2 实验结果与分析
2.1 变形条件对变形抗力的影响
2.1.1 变形程度对变形抗力的影响
图1(a)和(b)为不同变形温度和不同应变速率下Fe-11Mn-10Al-0.9C低密度钢真应力-应变曲线.从图中可以看出,在变形初始阶段,应力迅速提升,呈现明显的加工硬化现象;这是由于变形开始后随着应变的增加,位错迅速增殖,同时位错间的相互作用限制了位错的进一步运动所致.当应力增大到一定值时,应力增加趋于缓和并在达到峰值后缓慢下降,说明此刻达到软化(动态回复或动态再结晶)的临界应变,触发软化机制.在达到峰值应力之后,变形进入加工硬化和软化相互竞争的动态过程.随着应变程度的增加,加工硬化和软化的效果达到动态平衡,应力进入相对稳定的阶段.

图1 Fe-11Mn-10Al-0.9C低密度钢真应变-应力曲线Fig.1 True strain-stress curves of Fe-11Mn-10Al-0.9C low density steel
2.1.2 变形温度对变形抗力的影响
变形温度是变形抗力的重要影响因素.由图2不同变形量下变形抗力随变形温度的变化趋势可以看出,在应变速率一定的情况下,变形抗力随着变形温度的升高而降低,这主要是由于,变形温度升高会导致金属原子热振动振幅的增大,使滑移阻力减小,开动新的滑移系,从而降低变形抗力[6];同时,变形温度升高增大了空位原子扩散和位错进行攀移、交滑移的驱动力,使软化机制(动态回复和动态再结晶)容易发生[7].
2.1.3 应变速率对变形抗力的影响
图3为Fe-11Mn-10Al-0.9C低密度钢在应变量为0.1时不同变形温度条件下,变形抗力和应变速率间的变化关系.从图中可以看出,在变形温度相同的状态下,随着应变速率的增大,变形抗力逐渐增大.在应变速率更大的条件下,位错运动速度随之加快,需要更大的切应力,同时更高的应变速率导致在塑性变形过程中软化过程进行不充分,加剧了加工硬化,变形抗力必然提高[8].

图2 不同变形程度下Fe-11Mn-10Al-0.9C低密度钢变形抗力与变形温度的关系Fig.2 Relationships between deformation resistance and temperature of Fe-11Mn-10Al-0.9C low density steel at different true strains
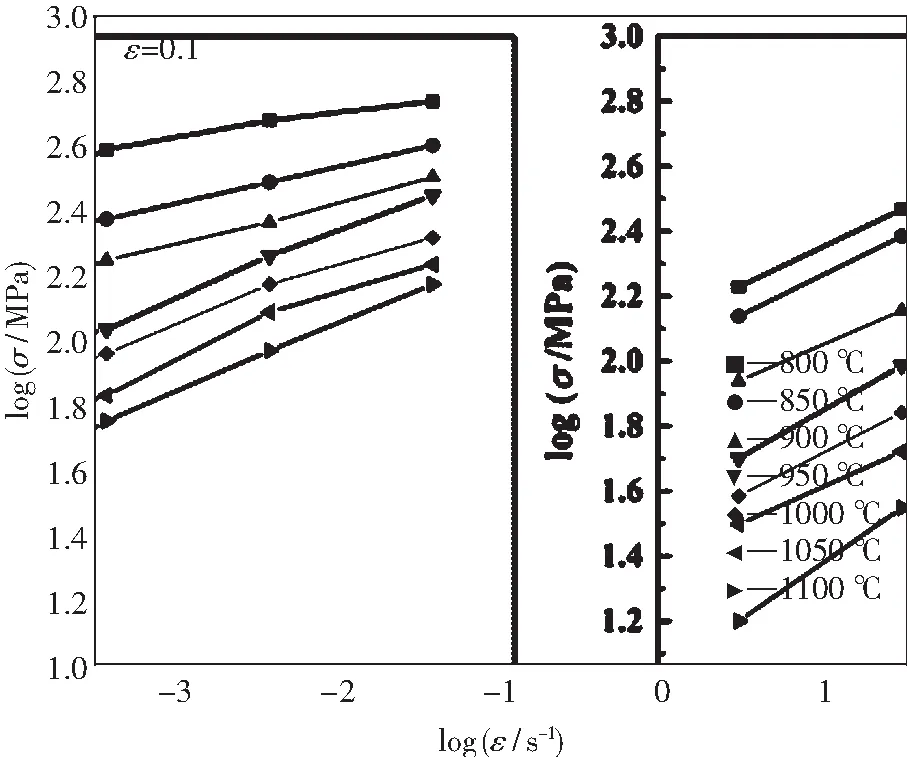
图3 Fe-11Mn-10Al-0.9C低密度钢真应变0.1时变形抗力与应变速率自然对数关系Fig.3 Natural logarithm relationships between deformation resistance and strain rate of Fe-11Mn-10Al-0.9C low density steel at true strain of 0.1
2.2 变形抗力模型
根据金属变形抗力数学模型建立的原则[9],通过对变形程度、变形温度和应变速率3个宏观因素对变形抗力的影响的分析,并根据Fe-11Mn-10Al-0.9C低密度钢35组数据进行曲线拟合回归分析和精度比较,最终确定其变形抗力模型为:
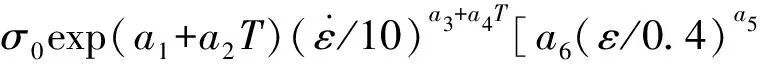
+(a6-1)(ε/0.4)]
(1)
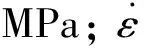
采用麦夸特法(Levenberg-Marquardt)和通用全局优化法[10],对热压缩试验数据按照公式
(1)进行非线性回归拟合,得到回归系数,如表1所示.

表1 Fe-11Mn-10Al-0.9C低密度钢变形抗力模型回归系数Table 1 Regression coefficient of deformation resistance model of Fe-11Mn-10Al-0.9C low density steel
将回归系数代入,得到Fe-11Mn-10Al-0.9C低密度钢变形抗力模型如下所示:

(2)
该模型回归分析的相关系数为0.967,说明该回归方程具有较好的曲线拟合特性.
利用公式(2)对材料的变形抗力进行预测,其计算结果与热压缩实验实测值相比较,如图4所示,变形抗力模型计算值与实验值之间具有较好的吻合程度.为了进一步明确Fe-11Mn-10Al-0.9C低密度钢变形抗力模型的精确性,通过计算平均相对误差Δ来表述:
(3)
式中,Ei为热压缩实验实测应力值,Pi变形抗力模型计算值,N为计算所含数据个数.通过计算得到平均相对误差值为4.12%,这说明采用该变形抗力模型可以较为精确地计算Fe-11Mn-10Al-0.9C低密度钢的变形抗力.
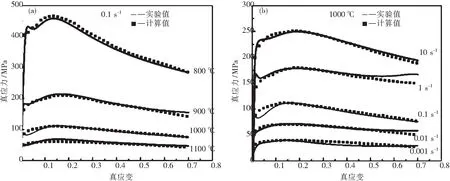
图4 Fe-11Mn-10Al-0.9C低密度钢实验值与计算值对比Fig.4 Comparisons between experimental and calculated value of Fe-11Mn-10Al-0.9C low density steel
2.3 热加工图
Prasad等人[11-13]提出动态材料学模型,材料加工过程可被看作是一个能量耗散系统,将大塑性变形连续介质力学和耗散微观组织机构演变建立联系,成功地描述了材料在热变形过程中组织的动态响应.根据耗散结构理论[12-13],在给定温度下的热加工过程中,耗散功率P由两部分组成:塑性变形所引起的功率耗散,其中大部分能量转变为热能,剩余部分以晶体缺陷能的形式存储的耗散量G,以及在变形过程中与微观组织演变,如动态回复、动态再结晶、内部裂纹、位错、相变等有关的耗散协量J,如下式所示:
(4)
上述两种能量所占比例,由一定应力下的应变速率敏感指数m分配,m可表示为:
(5)
当m值增大到1时,材料处于理想线性耗散状态,耗散协量达到最大值Jmax=P/2[12-13].消耗过程非线性与理想线性耗散的比值即功率耗散因子η,描述的是热变形过程中因微观组织演变所耗散的能量与线性消耗总能量的比值[12-13].其数学表达式为:
(6)
功率耗散因子随变形温度和应变速率的变化就构成了功率耗散图.然而,在功率耗散图中并不是η值越大,材料的可加工性能越好.因为在加工失稳区η值也可能会较高,所以应该先判断出材料的加工失稳区.
基于最大熵增原理,Prasad等人[14]提出应用于大应变塑性流变中的失稳判据ζ:
(7)
当ζ的值小于0时,发生不稳定流变过程.将功率耗散图和流变失稳图进行叠加构成热加工图.图5为Fe-11Mn-10Al-0.9C低密度钢真应变为0.7时的热加工图,图中等值线上的数值表示功率耗散因子η值,阴影部分表示失稳区.
在热加工图中,能量耗散率的值在高于30%时动态再结晶较为充分进行,该区域变性条件下具有较好的加工性能;然而钢的相变、析出或超塑性现象的发生也可能会导致能量耗散率的值过大[7].Fe-11Mn-10Al-0.9C低密度钢功率耗散因子η较大的值出现在较低的应变速率条件区域A中,在变形温度为800 ℃、应变速率为0.001 s-1功率耗散因子η达到最大值68%以上.由图5可以看出,Fe-11Mn-10Al-0.9C低密度钢的热加工图中的失稳区分别位于左上角和右上角区域,两区域对应着η值较小的区域,即变形温度为800~870 ℃、应变速率为0.05~10 s-1区域B,变形温度为950~1 100 ℃、应变速率为1~10 s-1区域C.
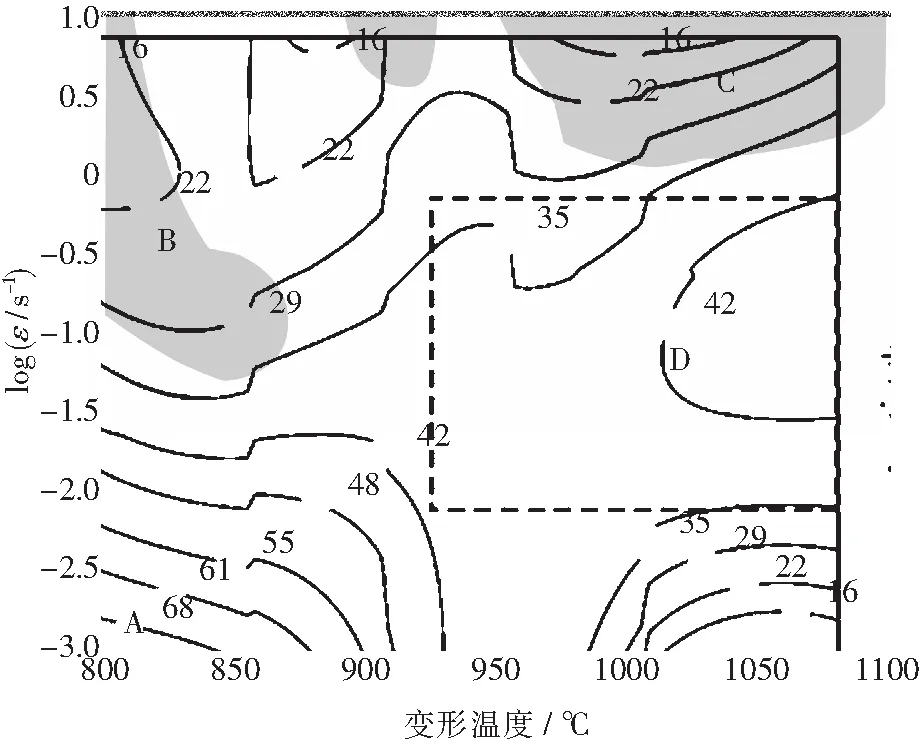
图5 Fe-11Mn-10Al-0.9C低密度钢在真应变0.7时的热加工图Fig.5 The processing map of Fe-11Mn-10Al-0.9C low density steel at true strain of 0.7
图6为Fe-11Mn-10Al-0.9C低密度钢在真应变0.7的热变形组织照片.图6(a)对应图5中的A区域,在变形温度为800 ℃、应变速率为0.001 s-1时,在该较低变形温度缓慢的变形过程中发生了共析反应,奥氏体→铁素体+κ碳化物,κ碳化物的形成和长大导致功率耗散因子η增大达到较高的数值.图6(b)对应图5中的B区域,在变形温度为800 ℃、应变速率为10 s-1条件下,部分奥氏体发生动态再结晶,同时,细小的κ碳化物分布于再结晶晶粒界面位置,降低了晶界聚合力,在热变形过程中容易导致裂纹的萌生引发失效[15].图6(c)对应图中5的C区域,在变形温度为1 050 ℃、应变速率为10 s-1时,高应变速率使变形过程的绝热温升没有足够的时间扩散,局部温度和变形储能的增加促使在奥氏体晶界位置发生动态再结晶,形成链状组织造成局部流变,导致不均匀变形[16].图6(d)对应图中5的D安全区域,功率耗散因子η值大于35,在变形温度为1 050 ℃、应变速率为0.01 s-1时,动态再结晶充分进行,形成均匀细小的等轴晶粒.
结合热加工图与热变形组织的分析可知,热加工过程应选择功率耗散因子较高的区域,同时应避开失稳及析出物产生的区域.因此,Fe-11Mn-10Al-0.9C低密度钢的最佳热加工条件为变形温度950~1 100 ℃、应变速率0.01~1 s-1的区域.
3 结 论
(1)分析了变形程度、变形温度和应变速率对Fe-11Mn-10Al-0.9C低密度钢变形抗力的影响.变形开始时,变形抗力随应变量迅速增大,由于动态回复和再结晶的发生,在达到峰值后逐渐下降,在加工硬化和软化效果的平衡下趋于稳定.变形抗力随着应变速率增加而增大,随变形温度的升高而降低.
(2)建立了变形抗力模型,与实测值比较,拟合程度较好.模型的平均相对误差值为4.12%,表明预报精度较高,具有较高的工程应用价值.
(3)建立了热加工图,结合不同变形条件下的热变形组织,对热加工图的功率耗散因子峰值区和失稳区进行分析,最佳热加工窗口为变形温度950~1100 ℃、应变速率0.01~1 s-1的区域.

图6 Fe-11Mn-10Al-0.9C低密度钢在真应变0.7时不同热变形条件下的热变形组织Fig.6 Hot deformation microstructures of Fe-11Mn-10Al-0.9C low density steel at true strain of 0.7 (a)—800 ℃/0.001 s-1; (b)—800 ℃/10 s-1; (c)—1 050 ℃/10 s-1 ; (d)—1 050 ℃/0.01 s-1

