基于左特征向量配置的结构声主动控制

白 金, 黎 胜,2, 夏茂龙

(1. 大连理工大学 工业装备结构分析国家重点实验室 船舶工程学院, 大连 116024;2. 高新船舶与深海开发装备协同创新中心, 上海 200240)

结构声主动控制是结构振动辐射声场控制的研究重点之一[1-3]。结构声主动控制从结构振动与声辐射的关系出发，采用次级振源来进行结构声的主动控制，其实质是将振动主动控制应用到结构声辐射控制中，所以，结构声主动控制的研究进展是与振动主动控制的研究进展息息相关的[4]。闭环振动系统的动态特性可以通过求解振动系统的极点、右特征向量和左特征向量获得[5]：极点包含了振动系统的固有频率和阻尼信息；右特征向量即为模态振型，振动系统的响应由各阶模态振型叠加而成；左特征向量则代表了系统抵抗外部激励的能力，即模态被激励的能力，当左特征向量与激励力向量正交时，与该阶左特征向量对应的振动模态就不会被激发出来。因此，通过对左特征向量的配置可以实现对结构振动的主动控制。Choi等[6]采用最小二乘法将闭环系统的左特征向量配置成与激励力向量正交且与控制力平行的形式，在较小的能量消耗下闭环系统的振动响应得到有效降低。Choi[7]采用最小二乘法同时对闭环系统的左特征向量和模态振型进行配置，使左特征向量与激励力向量正交，而模态振型与输出矩阵正交，闭环系统输出点的振动响应得到大幅降低。目前，基于左特征向量的结构声主动控制的研究仍然比较少。Wu等[8]采用自适应特征向量优化算法，求出能使噪声抑制性能指标(Sound Suppression Performance Index)最小的最优左、右特征向量组合，并以此为目标对闭环系统进行特征结构配置，得到了较好的降噪效果。Wu等[9]通过对振动系统的左、右特征向量进行配置，将闭环系统的振动模态控制为弱辐射模态，并使受控后的左特征向量与激励力向量正交，同样得到了较好的降噪效果。本文采用耦合模态空间控制[10](Dependent Modal Space Control)方法，将闭环系统的左特征向量配置成与激励力向量正交的形式，通过降低结构的振动水平，实现了结构振动声辐射的主动控制。本文提出的结构声主动控制方法具有物理意义明确、实施过程简单、声辐射抑制效果好的特点。以矩形简支板为例对本文提出的结构声主动控制方法进行了数值仿真，结果表明闭环系统的振动声辐射得到了有效降低。

1 闭环系统的控制方程及其左、右特征向量

含有外部激励力和控制力的结构动力学方程可以写作

(1)

将控制力与振动结构考虑为一个整体，构成闭环系统，则式(1)可以写成

(2)

式中：[Mc]、[Cc]和[Kc]分别为闭环系统的等效质量阵、等效阻尼阵和等效刚度阵，其具体表达式由控制系统的输入与输出之间的传递关系、即控制律决定。比如采用速度反馈控制律，则输入为速度响应，输出为阻尼控制力。式(2)实质上是将式(1)中的控制力分解为相应的惯性力、阻尼力和弹性力，并将其等效为对应的质量、阻尼和刚度。通过求解与式(2)对应的特征值问题

(3)

(4)

由式(3)和式(4)可得相同的n对特征值s，将特征值s代入式(3)，可得右特征向量矩阵(即模态振型矩阵)

(5)

将特征值s代入式(4)，可得左特征向量矩阵

(6)

若[Mc]、[Cc]和[Kc]不为对称阵，则[Φc]和[Ψc]也就不相同。闭环系统位移响应可以表示为

(7)

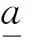
(8)

式中

[Hc]=

(9)

根据左特征向量的性质[11]可知[H]为对角阵，即模态振型矩阵[Φc]和左特征向量矩阵[Ψc]可将式(2)解耦。则有：

[H]ii=

(10)

(11)

2 左特征向量与模态振型的关系

[Φcm]=[Φm][W]

(12)

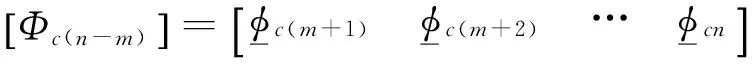
[Φc(n-m)]=[Φn-m]

(13)

振动系统的模态振型矩阵与左特征向量矩阵具有如下关系

[Φ]-T=[Ψ]

(14)

[Φc]-T=[Ψc]

(15)

式中：[Φ]和[Ψ]分别为开环系统的模态振型矩阵和左特征向量矩阵。将模态振型矩阵和左特征向量矩阵分成前m阶和后n-m阶两部分：

[Φ]=[[Φm] [Φn-m]]

(16)

[Φc]=[[Φcm] [Φc(n-m)]]

(17)

[Ψ]=[[Ψm] [Ψn-m]]

(18)

[Ψc]=[[Ψcm] [Ψc(n-m)]]

(19)

结合式(12)、式(13)、式(16)和式(17)得：

[Φc]=[[Φcm] [Φc(n-m)]]=[[Φm][W] [Φn-m]]=

(20)

由式(20)得：

(21)

将式(14)和式(15)代入式(21)得：

(22)

将式(18)和式(19)代入式(22)得：

[[Ψcm] [Ψc(n-m)]]=[[Ψm] [Ψn-m]]×

(23)

即：

[Ψc(n-m)]=[Ψn-m]

(24)

[Ψcm]=[Ψm][WL]

(25)

[WL]=[W]-T

(26)

由此可知，当开环系统和闭环系统的模态振型满足式(12)和式(13)时，则开环系统和闭环系统的左特征向量就会满足式(24)、式(25)和式(26)。即，闭环系统的前m阶左特征向量[Ψcm]为开环系统前m阶左特征向量[Ψm]的线性组合，闭环系统的后n-m阶左特征向量[Ψc(n-m)]与开环系统的后n-m阶左特征向量[Ψn-m]相等，且线性转换矩阵[WL]和[W]满足关系式(26)。因此，若想将闭环系统的前m阶左特征向量配置成与激励力向量正交的形式，可以先将开环系统的前m阶左特征向量[Ψm]通过线性组合构造出与激励力向量正交的闭环系统的前m阶目标左特征向量[Ψcm](即求出线性转换矩阵[WL])，然后经式(26)得到线性转换矩阵[W]，进而由式(12)得到闭环系统的前m阶目标模态振型[Φcm]，最后以[Φcm]为控制目标采用耦合模态空间控制方法实施主动控制，则闭环系统的前m阶左特征向量[Ψcm]就会被配置成与激励力向量正交的形式。其实质上就是利用系统的模态振型与左特征向量之间的关系，通过配置系统的模态振型来配置系统的左特征向量。

3 与激励力向量正交的左特征向量构造方法

(27)

式(27)可以写成

k1WL1+k2WL2+…+knWLm=0

(28)

(29)

(30)

将闭环系统的前m阶目标左特征向量[Ψcm]分为前m-1阶和后1阶两部分

(31)

在这里，我们取[Ψm]的第m阶向量作为闭环系统的第m阶目标左特征向量，即

(32)

由式(30)、式(31)和式(32)可得：

[Ψm][WL]

(33)

式中

(34)

(35)

因此，由本文构造的目标左特征向量[Ψcm]只有前m-1阶才满足与激励力向量正交的条件，这在实际应用中是需要特别注意的。

4 耦合模态空间控制方法

(36)

基于左特征向量配置的结构声主动控制的实施步骤为

步骤1对开环系统进行模态分析和声辐射分析，在关心的频段内找出辐射能力较大的m阶模态[Φm]，及其相应的左特征向量[Ψm]；

步骤2运用3节中介绍的方法得到线性转换矩阵[WL]，再由式(26)得转换矩阵[W]；

步骤3确定控制力施加位置，由耦合模态空间控制方法得到反馈控制增益矩阵[G]；

5 数值仿真

以受垂向点力激励的矩形简支板为例进行基于左特征向量配置的结构声主动控制仿真。板长Lx=0.500 m，板宽Ly=0.350 m，板厚H=0.004 m，板密度ρs=7 850 kg/m3，杨氏模量E=2.1×1011N/m2，泊松比υ=0.3，各阶模态阻尼比均取为ξr=0.01，空气密度ρ=1.21 kg/m3，声速c=343 m/s，参考声功率为10-12W。板结构四边简支，坐标原点取在板的几何中心。激励力作用位置坐标为(x1,y1)=(0.100 m,0.050 m)，幅值为F=1 N。将板划分为20×14的单元网格，计算中有限元和边界元均采用四边形四节点等参单元和相同的网格划分，其中，有限元为基于Mindlin板弯曲理论的板元，边界元为基于板表面的Rayleigh积分。

(37)

由式(26)得线性转换矩阵[W]：

(38)

采用有效独立法[13]选取5个控制点力，施加位置示于图 1。有效独立法通过逐步删除有效独立向量中最小值对应的自由度，来优化Fisher信息矩阵，使得各目标模态向量之间在尽可能少的位置点情况下保持线性独立，从而使用较少的位置点获得到更多的的模态信息。由耦合模态空间控制方法得到控制增益矩阵[G]。由式(36)得到反馈控制力，对结构实施结构声主动控制。由于开环系统的质量阵、刚度阵和阻尼阵都是对称阵，则开环系统的左、右特征向量相同，开环系统的第1、4、8阶模态振型示于图 2。闭环系统第1、4、8阶模态振型和左特征向量示于图 3。开环系统和闭环系统的前8阶固有频率、阻尼比和左特征向量与激励力向量内积分别示于表 1和表 2。

图1 控制力施加位置(■)和激励力作用位置(★)

由于闭环系统的等效阻尼阵和等效刚度阵不再对称，第1、4、8阶模态振型和左特征向量不相同(见图 3)。从表 1和表 2可以看到，闭环系统的第1、4阶左特征向量与激励力向量内积为零，达到了控制目的。同时，受控前后振动系统的其它阶固有频率、阻尼比和左特征向量与激励力向量的内积没有变化。

开环系统和闭环系统第1、4、8阶振动模态的模态速度幅值示于图 4。可以看到，闭环系统的第1、4阶振动模态的模态速度幅值极小，接近于零，说明激励力无法激发闭环系统的第1、4阶振动模态。开环系统和闭环系统的辐射声功率曲线示于图 5。可以看到，简支板的辐射声功率得到了有效降低。与开环系统相比，闭环系统的辐射声功率曲线在第1、4阶固有频率处的波峰消失。但是在第8阶固有频率附近闭环系统的辐射声功率高于开环系统的辐射声功率。这是由于本文提出的方法在对[Φcm]中的m个左特征向量进行配置时，最多只能将其中的m-1个左特征配置成与激励力向量正交的形式(第3节中有说明)。在本算例中，对闭环系统的第1、4、8阶左特征向量进行配置，只保证了配置后的第1、4阶左特征向量与激励力向量正交，配置后的第8阶左特征向量与开环系统的第8阶左特征向量相同，不与激励力向量正交。由式(38)可以看出，闭环系统的第8阶模态振型为开环系统的第1、4、8阶模态振型的线性组合。即，施加控制力后，振动系统的第8阶左特征向量没有改变，但第8阶模态振型发生了改变，这也就无法保证在第8阶固有频率附近闭环系统的辐射声功率低于开环系统，这在实际应用中是要特别注意的。

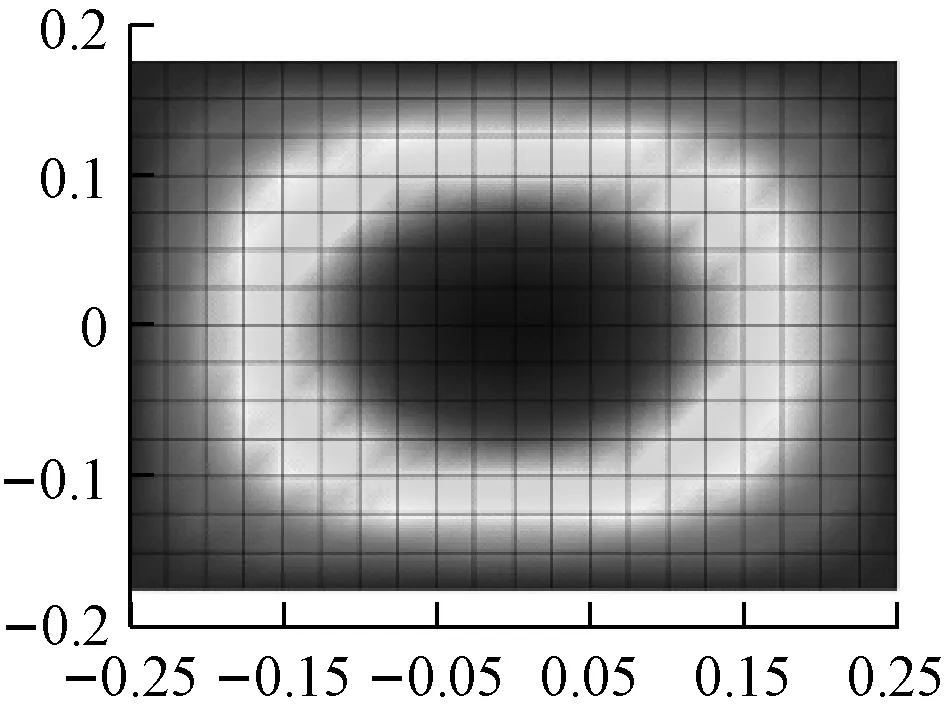
(a) 开环系统第1阶模态振型

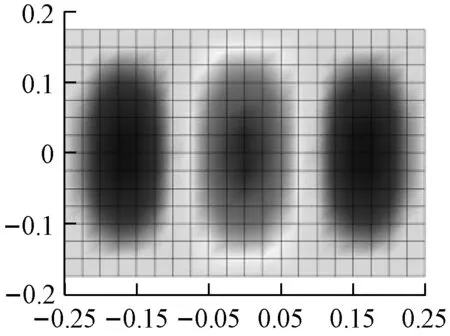
(b) 开环系统第4阶模态振型

(c) 开环系统第8阶模态振型

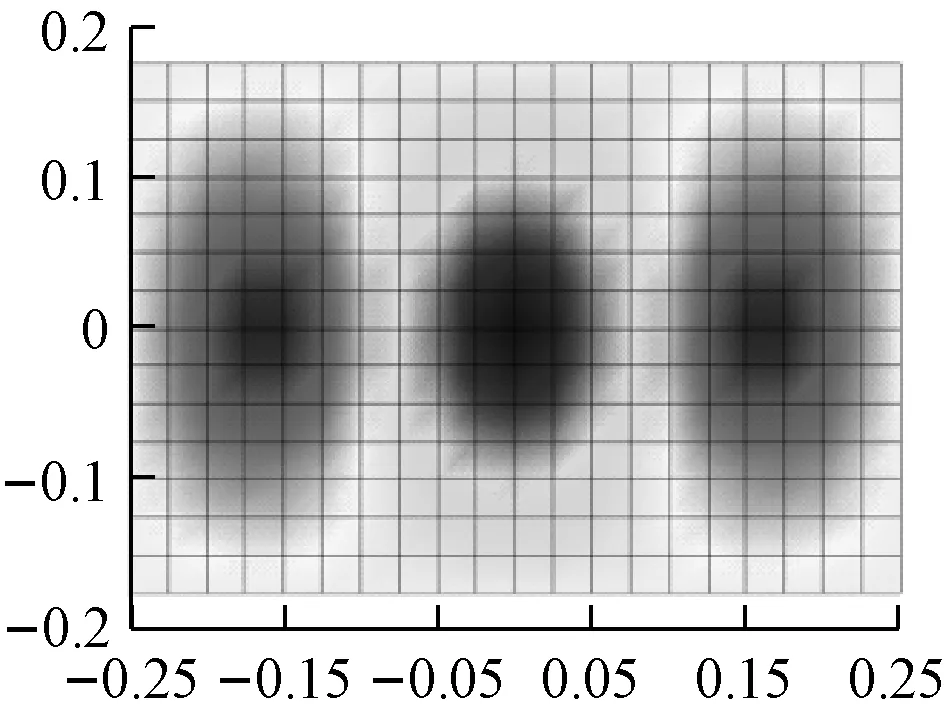
(a) 闭环系统第1阶模态振型

(b) 闭环系统第4阶模态振型

(c) 闭环系统第8阶模态振型

(d) 闭环系统第1阶左特征向量

(e) 闭环系统第4阶左特征向量

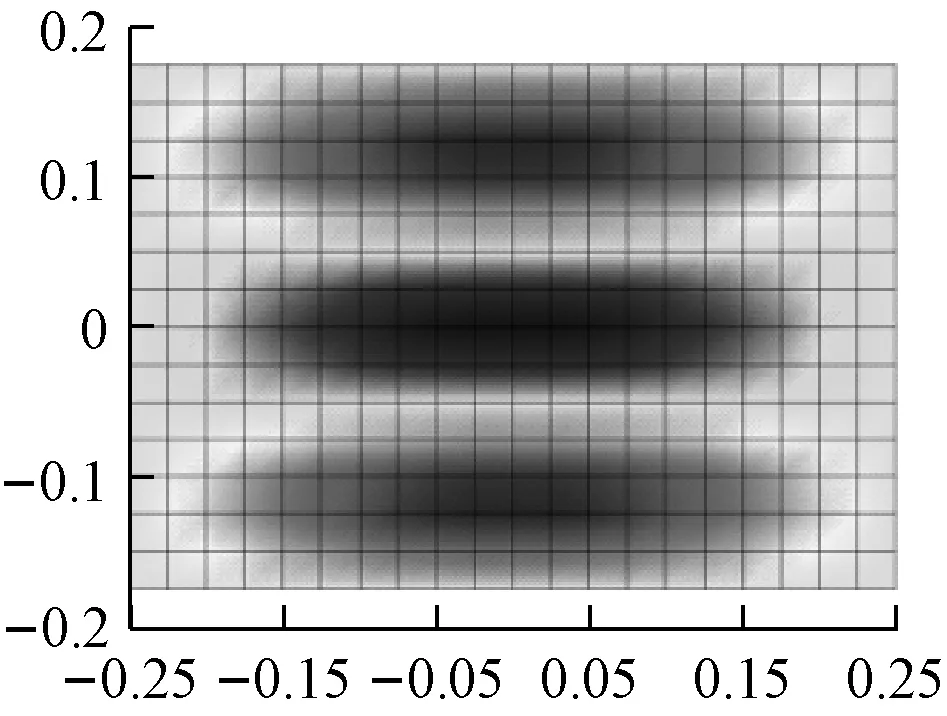
(f) 闭环系统第8阶左特征向量

Tab.1Thefirsteightnaturalfrequencies,dampingratiosandinnerproductsoflefteigenvectorandexcitationforcevectorofopenloopsystem

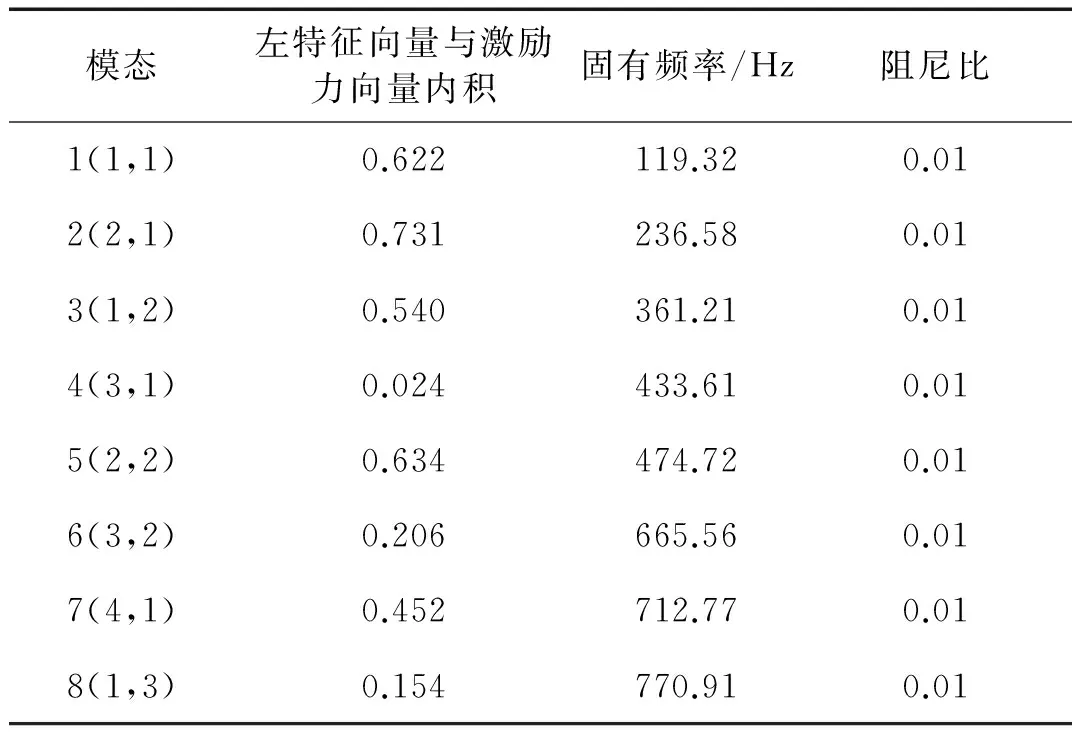
模态左特征向量与激励力向量内积固有频率/Hz阻尼比1(1,1)0.622119.320.012(2,1)0.731236.580.013(1,2)0.540361.210.014(3,1)0.024433.610.015(2,2)0.634474.720.016(3,2)0.206665.560.017(4,1)0.452712.770.018(1,3)0.154770.910.01

表2闭环系统前8阶固有频率、阻尼比和左特征向量与激励力向量内积

Tab.2Thefirsteightnaturalfrequencies,dampingratiosandinnerproductsoflefteigenvectorandexcitationforcevectorofclosedloopsystem

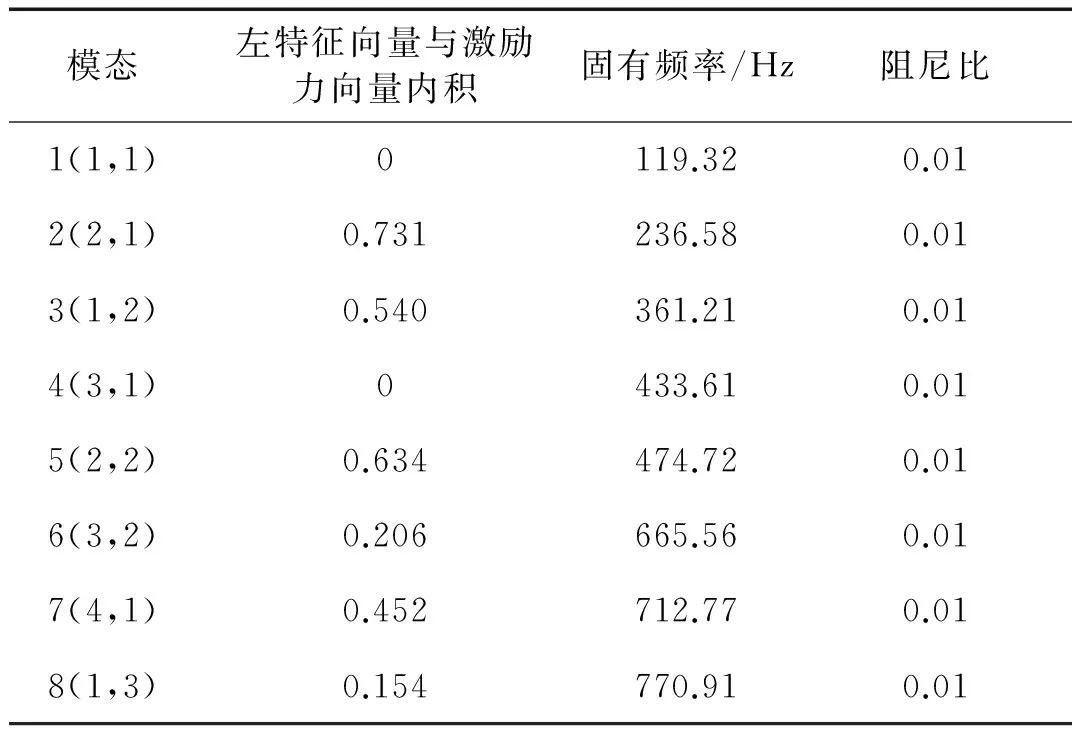
模态左特征向量与激励力向量内积固有频率/Hz阻尼比1(1,1)0119.320.012(2,1)0.731236.580.013(1,2)0.540361.210.014(3,1)0433.610.015(2,2)0.634474.720.016(3,2)0.206665.560.017(4,1)0.452712.770.018(1,3)0.154770.910.01

图4 开环系统和闭环系统第1、4、8阶振动模态速度幅值

6 结 论

本文结合耦合模态空间控制方法，通过将闭环系统的左特征向量配置成与激励力向量正交的形式，实现了基于左特征向量配置的结构声主动控制。推导了振动系统的左特征向量与模态振型之间的关系，得出当闭环系统的模态振型为开环系统的模态振型的线性组合时，闭环系统的左特征向量也为开环系统的左特征向量的线性组合的结论。构造了与激励力向量正交的目标左特征向量，以该左特征向量对应的模态振型为控制目标，采用耦合模态空间控制方法，间接实现了对闭环系统的左特征向量的配置，最终实现了低频结构振动声辐射的主动控制。最后以矩形简支板为例对本文提出的结构声主动控制方法进行了数值仿真，仿真结果验证了本文提出的基于耦合模态空间控制方法通过闭环系统左特征向量配置进行结构振动声辐射控制的有效性。

[1] FULLER C R, ELLIOTT S J, NELSON P A. Active control of vibration[J]. Physics Today, 1997, 50(50): 313-326.

[2] FULLER C R, ROGERS C A, ROBERTSHAW H H. Control of sound radiation with active/adaptive structures[J]. Journal of Sound & Vibration, 1992, 157(1): 19-39.

[3] FULLER C R, HANSEN C H, SNYDER S D. Experiments on active control of sound radiation from a panel using a piezoceramic actuator[J]. Journal of Sound & Vibration, 1991, 150(2): 179-190.

[4] 黎胜. 水下结构声辐射和声传输的数值分析及主动控制模拟研究[D].大连： 大连理工大学, 2001：8-9.

[5] WU T Y, WANG K W. Active vibration isolation via simultaneous left right eigenvector assignment[J]. Smart Materials & Structures, 2008, 17(17): 288-294.

[6] CHOI J W, KIM Y, KANG T, et al. Design of an effective controller via disturbance accommodating left eigenstructure assignment[J]. Journal of Guidance Control & Dynamics, 1993, 18(18): 347-354.

[7] CHOI J W. A simultaneous assignment methodology of right/left eigenstructures[J]. IEEE Transactions on Aerospace & Electronic Systems, 1998, 34(2): 625-634.

[8] WU T Y, CHUNG Y L. Structural acoustic reduction via piezoelectric actuation and adaptive eigenvector optimization algorithm[J]. Journal of Intelligent Material Systems & Structures, 2010, 21(21): 1797-1808.

[9] WU T Y, WANG K W. Reduction of structural acoustic radiation via left and right eigenvector assignment approach[J]. Journal of Intelligent Material Systems & Structures, 2009, 20(20): 2173-2186.

[10] SERRA M, RESTA F, RIPAMONTI F. Dependent modal space control[J]. Smart Materials & Structures, 2013, 22(10): 622-629.

[11] 邱吉宝，向树红，张正平. 计算结构动力学[M]. 合肥: 中国科学技术大学出版社, 2009:246-252.

[12] 黎胜，赵德有. 结构声辐射的振动模态分析和声辐射模态分析研究[J]. 声学学报, 2004, 29(3): 200-208.

LI Sheng, ZHAO Deyou. Research on modal analysis of structural acoustic radiation using structural vibration modes and acoustic radiation modes [J]. Acta Acustica, 2004, 29(3): 200-208.

[13] 刘伟，高维成，李惠，等. 基于有效独立的改进传感器优化布置方法研究[J]. 振动与冲击, 2013, 32(6): 54-62.

LIU Wei, GAO Weicheng, LI Hui, et al. Improved optimal sensor placement methods based on effective independence [J]. Journal of Vibration and Shock, 2013, 32 (6): 54-62.