基于八区域的简单多边形顶点凸凹性识别算法

薛 理 杨树文 王中辉 张 珊 马吉晶

(兰州交通大学测绘与地理信息学院 甘肃 兰州 730070) (甘肃省地理国情监测工程实验室 甘肃 兰州 730070)

0 引 言

简单多边形顶点凸凹性的判断是计算机图形学的基本问题，随着计算机的发展，在模式识别、图像处理、曲面插值等方面应用广泛[1]。因此，如何快速、准确地判断多边形顶点凸凹性具有重要意义。

学者们已在该研究领域进行了大量卓有成效的研究，提出了多种识别算法[1-6]：如面积判断法[1]、叉积判断法[2]和象限判断法[3]等。其中，面积判断法首先通过极值点确定多边形方向，进而计算各个顶点的有向面积来判断顶点的凸凹性；叉积判断法对每条边定义矢量方向，利用各点相邻两条矢量的矢量叉积来确定顶点凸凹性；象限判断法先假设多边形为逆时针方向，然后根据角两边在直角坐标系四个象限内的特性确定顶点内角的范围，进而判断顶点的凸凹性。

上述多边形顶点凸凹性的判断算法多是通过定量的方式来判断顶点的凸凹性，虽然这些算法的正确率高、思路简洁，但计算量偏大，且未将定性与凸凹性联系起来。通过象限判断法来确定角度范围，进而将定性与凸凹性联系起来，达到判断的目的。该方法不仅思路清晰，而且能避免大量计算，提高算法效率。然而，象限法未能充分利用角的范围在直角坐标系内的特性，因此只能在一定程度上加快判断速度。

综上所述，本文将坐标系平面平均划分为八个区域来确定角度的范围，进而通过定性的方式确定顶点凸凹性，能够更充分地利用角的两边在平面坐标系内的特性，减少算法计算量。同时，该算法能够有效地判断多边形的方向，进一步提高算法的效率。

1 相关定义

为方便理解本文算法，在文献[1]的基础上给出如下定义：

定义1设存在多边形p1,p2,…,pi,pi+1,…,pn,p1，若任意相邻三点不在同一直线上，且任意相邻两边只相交于一个端点，不相邻两边不相交，则该多边形为简单多边形。

定义2如果简单多边形相邻的两边所形成的内角(即朝向多边形区域内的角)不大于180°，则该角为凸角，否则为凹角。

定义3设存在简单多边形p1,p2,…,pi,pi+1,…,pn,p1，如果沿p1,p2,…,pn,p1方向走，如果该多边形所围成的区域总在左侧，则称该多边形为逆时针多边形，否则为顺时针多边形。也可以通过计算y值最小值顶点相邻两边夹角来判断多边形的方向，详细步骤请看2.2节多边形方向的确定。

2 算法原理

2.1 平面的八区域

根据平面八区域的定义，给定线段op以端点o为坐标原点，x、y轴分别置于水平位置与竖直位置，取向右与向上的方向分别为x、y轴的正方向，形成平面直角坐标系。令线段op沿着顺时针方向转到x轴正方向所经过的角度为θ，并且θ从0°开始每隔45°为一个区域，比如第一区域内0°≤θ<45°，第二区域内45°≤θ<90°以此类推，将坐标系平面分为八个区域，如图1所示。

图1 平面八区域

2.2 多边形方向的确定

前人研究表明[7-8]，简单多边形中y最小值的顶点一定为凸顶点，即内角小于180°。根据这一特性，先确定y最小值顶点，再按照一定的方向分析最小值顶点两边夹角的范围，进而判断简单多边形的方向。其具体实现过程如下所示：

在简单多边形p1p2p3p4p5p6p1中(如图2、图3)，p4为y最小值的顶点，该点的内角必定小于180°。沿着p4p3边顺时针转到p4p5边形成的角度为θ，由于该多边形为简单多边形因此θ不会等于0°、180°或360°，判断θ的范围在2.3节详细介绍。如果该多边形方向为逆时针则θ小于180°如图2所示，如果多边形方向为顺时针则θ大于180°如图3所示，反之亦然。因此可得如果θ小于180°则多边形方向为逆时针，如果θ大于180°则多边形方向为顺时针。

图2 逆时针多边形 图3 顺时针多边形

2.3 顶点凸凹性判断方法

多边形分为逆时针多边形和顺时针多边形两种类型，只要了解其中一种多边形顶点的凸凹性判断方法，另外一种可以类推出来，因此，本文仅详细描述简单逆时针多边形中顶点凸凹性的判断方法。

设p1p2p3p4p5p6p7是一个简单逆时针多边形，判断顶点p4(x4，y4)的凸凹性，如图4所示。

图4 简单逆时针多边形

以p4为原点建立平面直角坐标系，x、y轴分别置于水平位置与竖直位置，取向右与向上的方向分别为x、y轴的正方向。以p4p3为起始边，沿着顺时针方向旋转到边p4p5所形成的角度为θ，则θ为顶点p4的内角，如图5所示。由于该多边形为简单多边形，因此θ不会等于0°、180°或360°。

图5 顶点p4的内角θ

由于p4p3位于第八区域，p4p5位于第六区域，由两边在平面八区域的特性容易得出角θ<180°，即p4为凸顶点。同时也可以得出，如果p4p5位于第一、二或三区域，则θ>180°，那么p4为凹顶点；如果p4p5位于第五、六或七区域，则θ<180°，那么p4为凸顶点。如果p4p5位于第四区域，需要判断p4p3和p4p5的斜率。如果(y3-y4)÷(x3-x4)<(y5-y4)÷(x5-x4)，即(y3-y4)× (x5-x4)>(y5-y4)×(x3-x4),则θ<180°，那么p4为凸顶点。如果(y3-y4)÷(x3-x4)>(y5-y4)÷(x5-x4)，即(y3-y4)× (x5-x4)<(y5-y4)×(x3-x4),则θ>180°，那么p4为凹顶点。如果p4p5位于第八区域，需要判断p4p3和p4p5的斜率。如果(y3-y4)÷(x3-x4)>(y5-y4)÷(x5-x4)，即(y3-y4)× (x5-x4)>(y5-y4)×(x3-x4),则θ<180°，那么p4为凸顶点。如果(y3-y4)÷(x3-x4)<(y5-y4)÷(x5-x4)，即(y3-y4)× (x5-x4)<(y5-y4)×(x3-x4),则θ>180°，那么p4为凹顶点。同理可以类推出p4p3位于其他区域内顶点p4的凸凹性。

如果多边形为顺时针方向，可根据θ′=360°-θ，由θ的范围推出θ′的范围，再根据θ′来判断顶点凸凹性。

3 算法描述和算法分析

3.1 算法描述

根据上述原理和算法，本文提出了改进的简单多边形顶点凸凹性识别算法，具体步骤如下：

Step1给定简单多边形pi(xi,yi),i=1,2,…,n,pn+1=p1，遍历所有顶点，求出y值最小值的顶点ymin=MIN(yi)。

Step2线段yminymin-1沿着顺时针方向旋转到线段yminymin+1的角度为θ，根据θ在八个区域内的特性判断其范围，如果θ<180°则多边形为逆时针多边形，否则为顺时针多边形。

Step3遍历每个顶点，利用角的两边在八区域内的特性判断顶点θi的范围，如果多边形为逆时针转到Step4，否则转到Step5。

Step4如果θi<180°，那么pi为凸顶点，否则为凹顶点，算法结束。

Step5如果θi<180°，那么pi为凹顶点，否则为凸顶点，算法结束。

3.2 算法分析与验证

通过2.3节提出的凸凹性判断方法可以看出，在多边形方向已知的情况下，对于一个顶点pi凸凹性的判断，在最有利的情况下，边pi-1pi在边pi+1pi左边或右边相邻的三个区域，则只需要六次判断即可；在最坏的情况下，边pi-1pi在边pi+1pi相对或同一区域，则需要判断斜率，增加两次乘法运算。即在边pi-1pi所在区域确定的情况下，pi+1pi在六个区域内只需判断，在余下两个区域内需要计算乘法。原有算法(文献[3]提出的算法)判断顶点pi凸凹性，在边pi-1pi所在象限确定的情况下，pi+1pi在相邻两个象限内只需判断，在另外两个象限内需要计算乘法[3]。因此新算法相对于原算法，更能有效地避免耗时的乘法运算。

论文采用C#编程实现多边形顶点凸凹性的判断，首先随机生成502、1 002和50 002个点，存储在Excel表中。然后假设每相邻三个点形成简单逆时针多边形的一个顶点，接着采用原算法A与本文算法B，在运行一万次的情况下判断每组数据的凸凹性。由于文献[3]提出的原算法已经和文献[1]、文献[6]的算法比较过，所以本文就不再比较。

通过实验得出改进后的算法和原算法结果一致，但在时间上，改进后的算法判断速度更快，两种算法时间对比如表1所示。由表1得出改进后的算法在数据相同情况下判断所需的时间是原算法所用时间的76%左右，且顶点越多提高的效率越明显。因此改进后算法具有更高的识别效率。

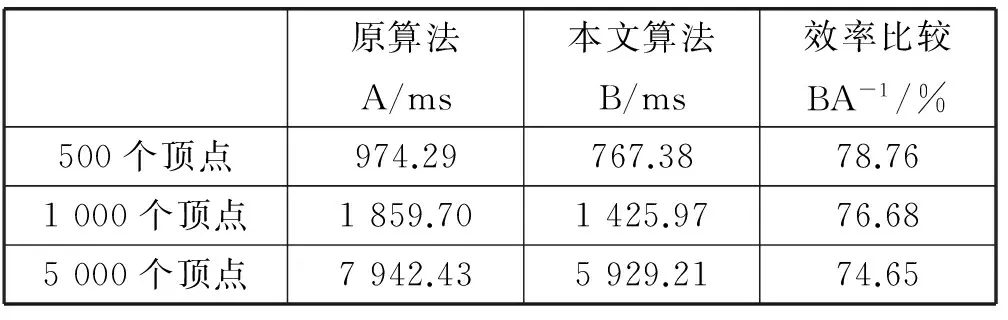
表1 原算法与本文算法对比

4 结 语

本文在四象限算法的基础上提出基于八区域的简单多边形顶点凸凹性识别算法。该算法利用角两边在八个区域内的特性，判断角度范围，进而判断顶点凸凹性，从而在一定程度上避免角度、面积或矢量叉积等定量分析所需的计算量。另一方面利用y值最小值顶点一定是凸顶点的特点和八区域方法判断多边形方向。该算法时间复杂度为O(n)，思路清晰，易于理解，而且计算量小，效率较高。实验表明改进后的算法，效率有明显的提高。

该算法的不足之处在于：1) 虽然算法利用定性的八区域方法判断顶点凸凹性，减少了耗时的乘法运算，但增加了判断运算。如何同时确定多个顶点的凸凹性，去掉多余的判断运算，有待于进一步分析；2) 该方法目前只适用于简单多边形，对于自相交等复杂多边形不适用，需要对该算法进一步改进，增加相应的规则，扩展算法的应用范围。

[1] 刘润涛.任意多边形顶点凹、凸性判别的简捷算法[J].软件学报,2002,13(7):1309-1312.

[2] 陈炳发,钱志峰,廖文和.简单多边形凸凹性自识别算法[J].计算机辅助设计与图报,2002,14(3):214-217.

[3] 魏东,朱功勤.任意多边形顶点凸、凹性判定的一种算法[J].合肥工业大学学报(自然科学版),2006,29(3):373-375.

[4] 陈亚婷,严泰来,朱德海.基于辛普森面积的多边形凹凸性识别算法[J].地理与地理信息科学,2010,26(6):28-30.

[5] 史万明.多边形顶点为凹、凸点的计算机判别方法[J].计算机辅助设计与图形学学报,1990(3):15-16.

[6] 马小虎,潘志庚,石教英.确定多边形凸凹顶点的快速算法及其应用[J].计算机工程与设计,1998(3):44-48.

[7] 闫浩文,王明孝,王中辉.计算几何[M].北京:科学出版社,2012.

[8] 陈国军,刘婧怡,黄莹莹.矢量与栅格结合的分块平面区域几何划分算法[J].系统仿真学报,2016,28(10):2460-2466.