不平衡数据分类研究及其应用

叶 枫 丁 锋

(浙江工业大学经贸管理学院 浙江 杭州 310012)

0 引 言

不平衡数据是指在数据集中各个类别所占的比例不均衡，即某些类别的数量是其他类别的几倍甚至几十倍。此类数据在实际应用中广泛存在，如在检测某种特定疾病[1]中，患该疾病的数量远远小于检查人数；网站防御[2]中，网络入侵的概率也远远小于正常访问的概率；在过滤垃圾邮件[3]中，垃圾邮件的数量小于一般邮件的数量等。诸如此类问题中，对于少数类的分类结果对实际应用异常重要，然而传统分类方法通常假定数据集是平衡的，因此对平衡数据的分类精确度较高，而对于不平衡数据的分类精确度却往往较低[4]，这使得研究不平衡数据的分类问题成为近些年数据挖掘研究的热点问题。

针对不平衡数据的分类问题，目前主要从算法层面和数据层面两方面来解决[5]：在算法层面主要是改进算法以适应不平衡数据的分类，如代价敏感学习、集成学习等。在不平衡数据分类中，少数类往往是分类的重点，代价敏感学习给予每个类别不同的权重，即代价，当分类器错分少数类时将付出更多的代价，从而有效地提高少数类的分类准确率。但在实际应用中，代价敏感学习存在代价往往需要人为设定[6]，算法没有普遍适用性等缺点。集成学习算法的思想则是多个分类器集成的分类效果比单个分类器效果更佳，从而将多个分类器的分类结果进行组合，提高分类效果。数据层面主要针对的是数据处理，改变数据结构，较为常用的是过抽样和欠抽样技术。过抽样主要增加少数类样本，使少数类和多数类达到平衡。SMOTE方法是较为经典的过抽样数据处理方法[7]，但是可能带来数据过度拟合，使多数类与少数类的边界更加模糊[8]等缺点；而欠抽样主要删除多数类样本，使样本数据平衡，但随机删除多数类样本，存在使多数类样本特性丢失等风险[9]。

基于此，本文提出了一种基于k-means 聚类的欠抽样分类算法，利用k-means算法将样本数据进行聚类，剔除多数类样本与少数类样本的模糊边界点和噪声点，同时又能减少欠抽样过程中样本特性丢失的风险，以此缩小类别不平衡性，从而提高对少数类和整体数据的分类正确率。

1 相关知识

1.1 不平衡数据分类

传统分类方法以数据平衡化为基础，即分类的数据类别比例分布较为均匀，但是当实际数据不平衡性较为严重时，算法性能就较差。不平衡数据导致分类方法对少数类分类性能下降的原因如下：

1) 少数类样本的绝对稀少[10]；

2) 少数类与多数类比例过分悬殊，少数类样本相对稀少[11]；

3) 数据碎片问题[12]、噪声问题[11]；

4) 不恰当的评价方法[13]；

5) 少数类与多数类边界模糊，重叠度较高[14]。

如图1-图4所示。

图1 少数类样本绝对稀少

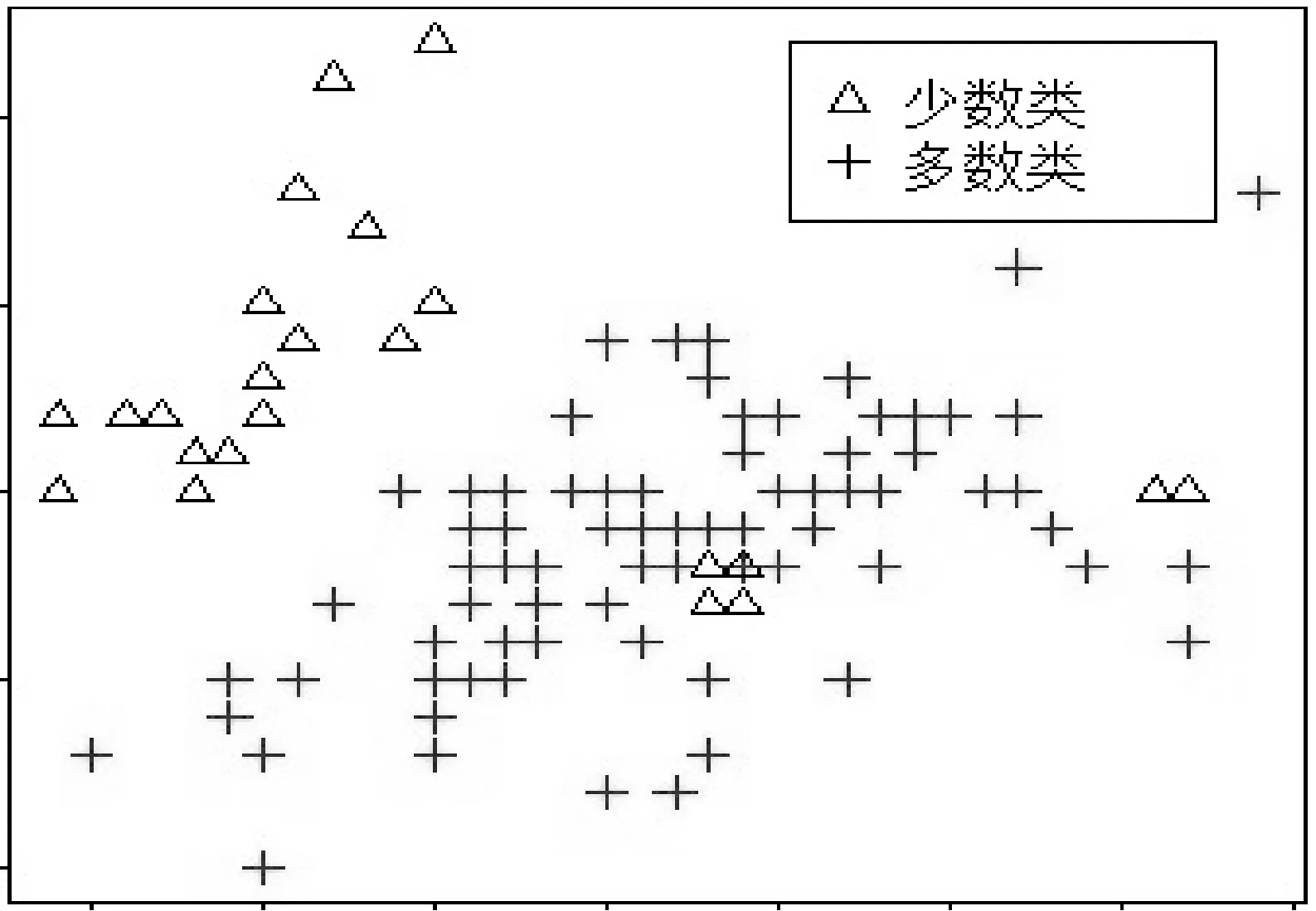
图2 碎片问题

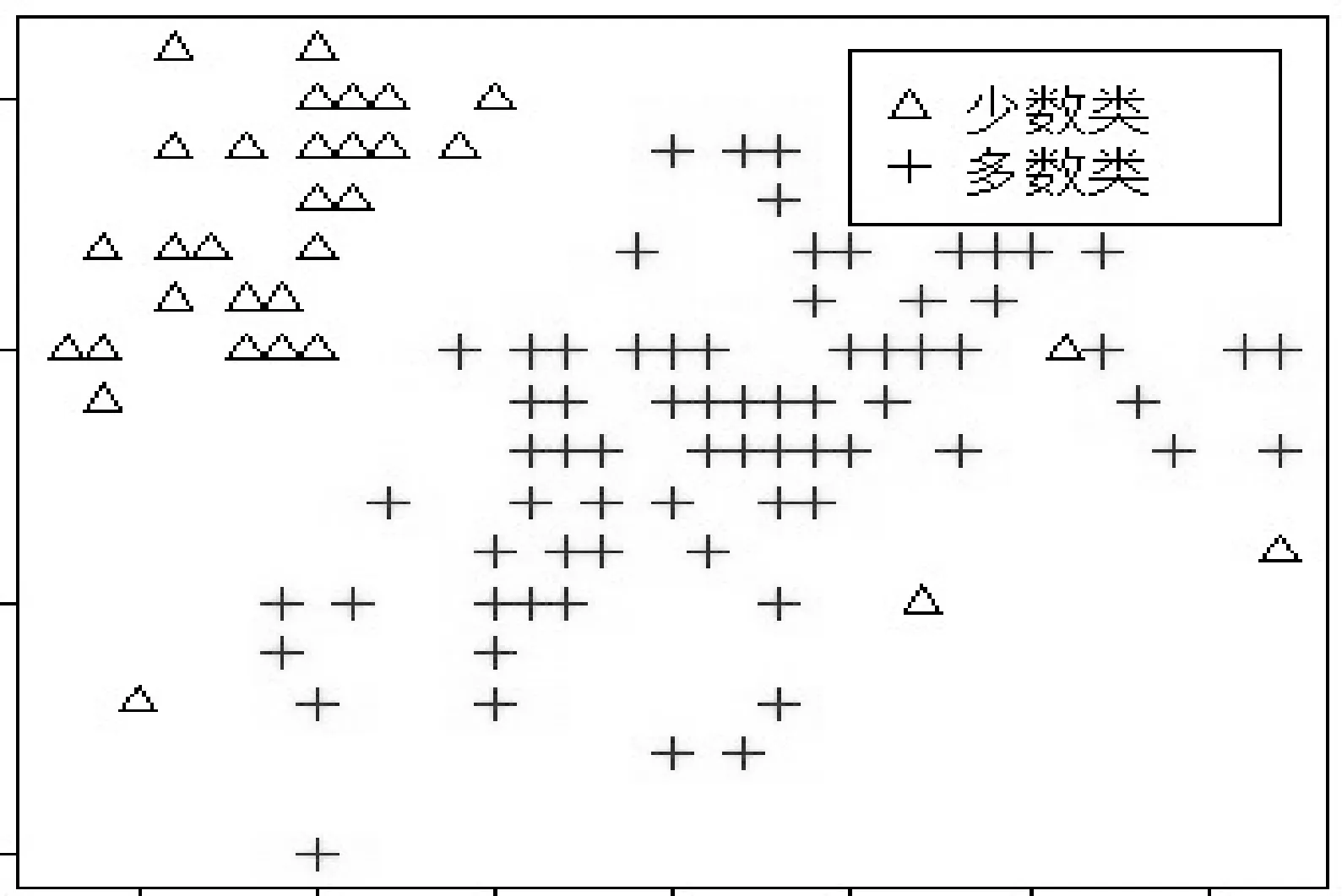
图3 噪音问题

图4 少数类与多数类边界重叠度高

而事实上，相关研究表明当不平衡数据具有足够多的样本时，少数类样本相对稀缺并不一定导致分类算法的性能下降[14]；当不平衡数据多数类和少数类的重叠度较低时，传统分类算法仍具有较好的分类属性，而当多数类与少数类具有较高重叠度时，分类算法的性能较差[15]。

1.2 k-means聚类算法

聚类属于无监督机器学习方法，即事先无需了解数据的分布情况，按照数据特征之间的相似度将数据自动划分成组，通过迭代，使组内样本之间的相识度尽可能高，而不同组的样本相似度尽可能低。聚类中的组亦称作簇。聚类系统将样本集数据经过聚类算法处理后，输出簇集。聚类可以初步评价数据的样本结构，用来研究各数据间的相关程度尤其适用。

k-means算法是一种经典的聚类算法，采用距离来衡量两个对象的相似程度(通常采用欧式距离)，距离越短，表示两个对象的相似度越高。k-means具体算法流程如下：

1) 将数据集D(X1,X2,…,Xn)划分为K个簇(C1,C2,…,Cn)。

2) 从数据集D中任意选取K个对象作为初始的簇心(V1,V2,…,Vn)。

3) 计算每一个对象与簇心的距离，通常使用误差平方和SSE(Sum of Squaerd Error)作为目标函数：

4) 将每个对象划分到距离最近的簇。

5) 重新计算每个簇中对象的均值，作为新的簇心。

6) 重复3-5步，直到k个簇中心不再发生变化。

1.3 不平衡数据分类算法评价指标

混淆矩阵是评价不平衡数据的常用工具，利用混淆矩阵可以获取分类准确率(Accuracy)、精度(Precision)、召回率(Recall)、F度量值等指标，混淆矩阵见表1。

表1 混淆矩阵

1) 分类准确率(Accuracy)：表示样本正确分类的个数与样本总数的比例。

2) 精度(Precision)：表示样本少数类正确分类的个数与分类为少数类总数的比例。

3) 召回率(Recall):表示样本少数类正确分类的个数与样本实际少数类个数的比例。

4) F值：表示精度和召回率的调和平均值。

其中β≥0,且常取1。

在分类方法中，经常使用准确率作为评价指标，但是在不平衡数据分类中，用准确率来评价分类性能的好坏是不恰当的。例如在具有1%的少数类样本中，将所有样本都预测为多数类的准确率为99%,尽管没分类出任何少数类。

精度和召回率是评价不平衡数据的常用指标，但若将每个样本都预测为少数类，分类的召回率将达到100%，但是精度将很差；相反，若正确分类的少数类很少，而又将多数类全部识别，则分类的精度将达到很高，但召回率却很低。而F值具有平衡精度和召回率的效果，F值越高，能保证精度和召回率都较高。

本文将采用召回率和F值两个较常用的评价指标。

2 基于k-means 的欠抽样分类算法

由于多数类问题普遍可以转为二分类问题，为简便起见，本文以二分类问题为研究对象。

针对欠抽样方法中，随机欠抽样单纯为使数据多数类和少数类达到平衡，删除多数类，而不能针对性地去除一些与少数类样本相似的多数类的问题。引入了k-means 聚类算法，先将样本集数据进行k-means 聚类，根据各样本之间的相似度将样本数据进行分组聚类，则样本属性相似度较高的数据将会形成一组，而不同组之间样本属性的相似度较低。从而可以有效地辨别出混杂在少数类中的多数类样本。如此可以更有效地删除多数类的噪声样本，降低多数类与少数类的重叠度和不平衡度，为避免由于聚类中心点随机选择，导致的聚类不同，我们进行多次聚类，以删除稳定的噪声和重叠点。同时，为降低丢失多数类特性的风险，我们引入删除比例因子λ，动态调整剔除个数。算法流程描述如下：

1) 将样本训练集k-means 聚类；

2) 计算每个簇的数目，为个数多的簇的每个对象标号kmaj，另一个簇的对象标号kmin；

3) 遍历多数类M，选出标号为kmin的对象；

4) 进行多次聚类，重复2-3步骤，将选出的多数类标号FM，并按出现概率正向排序；

5) 根据比例因子Mλ≤FM，删除选出的多数类，得到新样本集new_s；

6) 新样本集new_s 进行分类训练。

算法流程图见图5。

图5 KM-RF算法流程

3 实验及结论

3.1 数据处理

从UCI数据库中选取若干组数据集，参考以往文献，对具备多种类别的数据进行某些类的合并，数据集信息见表2(不平衡比为多数类比少数类的比例)。并将数据集按训练集和测试集7∶3的比例进行随机分配，对训练集进行标准化，进行k-means欠抽样处理，处理后训练集的信息见表3。

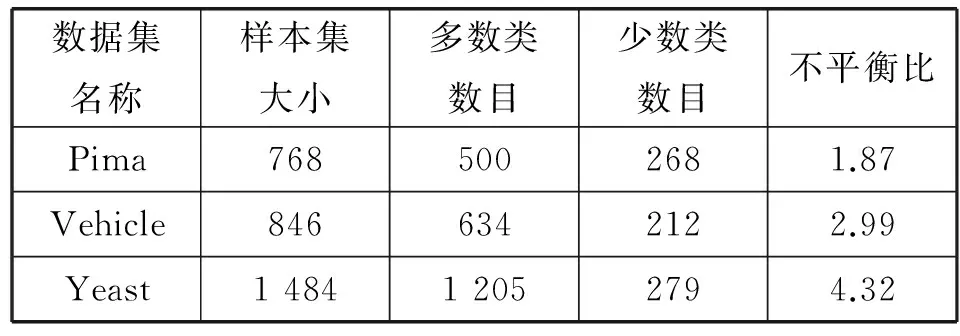
表2 UCI数据集信息

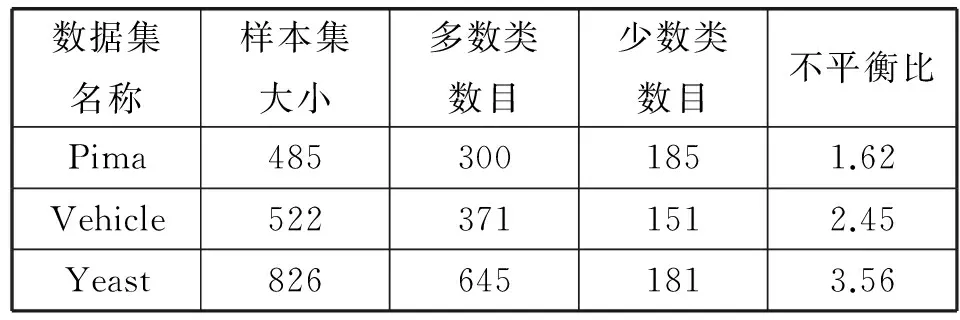
表3 k-means 欠抽样处理后训练集信息

3.2 实验及结论

随机森林集成多个决策树分类器，分类效果较单个分类器有所提高。故本实验采用随机森林作为分类算法，为使实验更具说服性，分别对比了三种算法的实验结果。

1) 未进行欠抽样处理直接利用随机森林算法分类。

2) 随机欠抽样处理后进行随机森林算法分类。

3) KM-RF算法。即基于k-means欠抽样的随机森林分类算法。且随机欠抽样的λ值与KM-RF的λ值相等。

图6，图7分别给出了不同数据集的Recall和F 值，为使结果更加客观，Recall和F值皆是10次实验，各取其平均值。实验结果表明KM-RF算法在Recall和F值上均好于其他两种算法，在对不平衡数据进行分类时具有良好的性能。

图6 三种算法的Recall对比

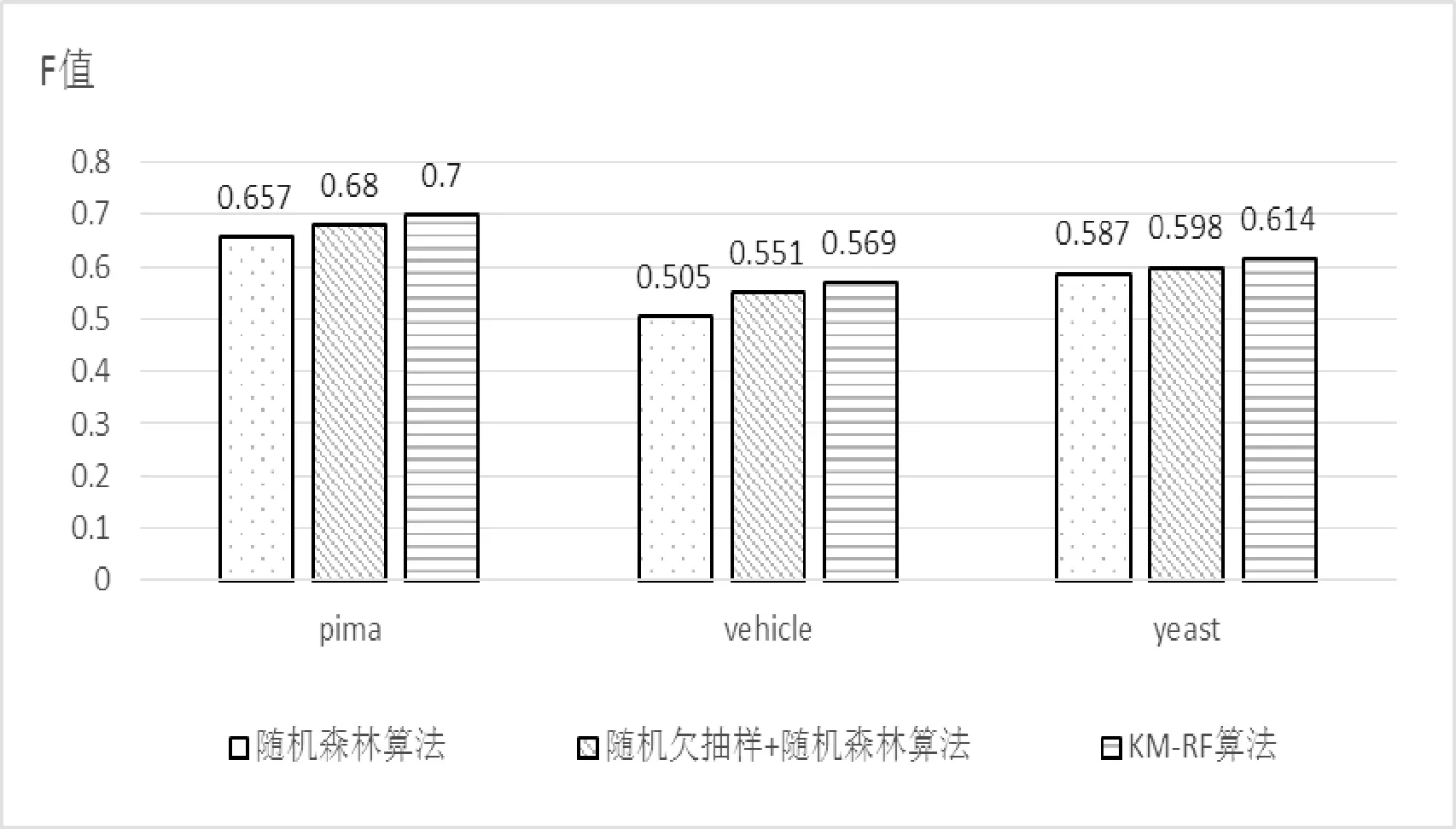
图7 三种算法的F值对比

4 原发性肺癌术后生存率预测

胸外科肿瘤患者，因其疾病的病、生理特性，多数需手术治疗，而肿瘤的特殊攻击性，患者伴有的一种或多种基础病，则加大了手术的风险性。故各级医师在术前需对患者进行综合风险评估，以确保患者的医疗性安全[16]。

医师对患者进行评估的项目除了患者的年龄，营养状况等基本信息，还包括患者病变器官的性质、病变的程度，手术切除器官范围等，以便决定患者对手术的耐受程度和预测术后生存质量[17]。

本实验原数据收集自弗罗茨瓦夫胸腔外科中心，以预测原发性肺癌术后生存率，数据包括2007年-2011年接受肺切除术的1 200例原发性肺癌患者，后经Maciej Zieba教授整理后发布，数据最终由470个实例组成，患者一年存活率与死亡率的不平衡比为5.71。图8给出了公布的部分数据和预测因子。表4给出了术前预测因子[18]。

图8 部分数据集

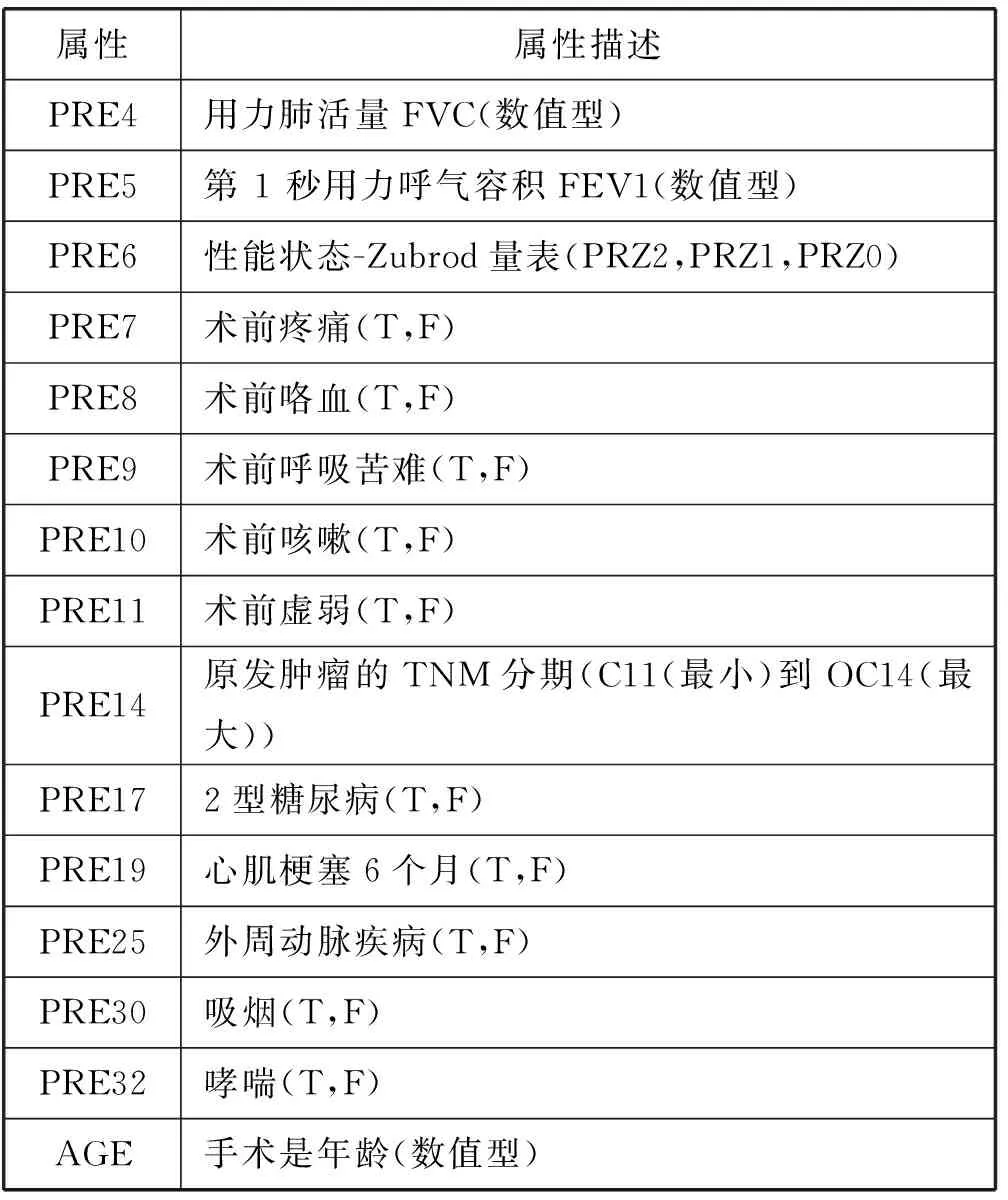
属性属性描述PRE4用力肺活量FVC(数值型)PRE5第1秒用力呼气容积FEV1(数值型)PRE6性能状态-Zubrod量表(PRZ2,PRZ1,PRZ0)PRE7术前疼痛(T,F)PRE8术前咯血(T,F)PRE9术前呼吸苦难(T,F)PRE10术前咳嗽(T,F)PRE11术前虚弱(T,F)PRE14原发肿瘤的TNM分期(C11(最小)到OC14(最大))PRE172型糖尿病(T,F)PRE19心肌梗塞6个月(T,F)PRE25外周动脉疾病(T,F)PRE30吸烟(T,F)PRE32哮喘(T,F)AGE手术是年龄(数值型)

将数据随机分配成7∶3，分别作为训练集和测试集。并依次进行直接随机森林算法分类；随机欠抽样处理后进行随机森林算法分类和KM-RF算法分类，实验过程同第三部分实验。表5给出了数据在各个状态下的多数类，少数类及其不平衡比。表6给出了实验结果：三种算法的少数类召回率和F值。

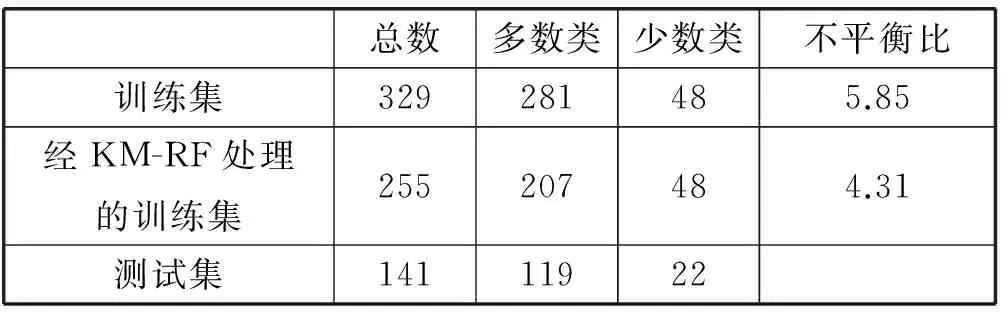
表5 处理后样本数据状态

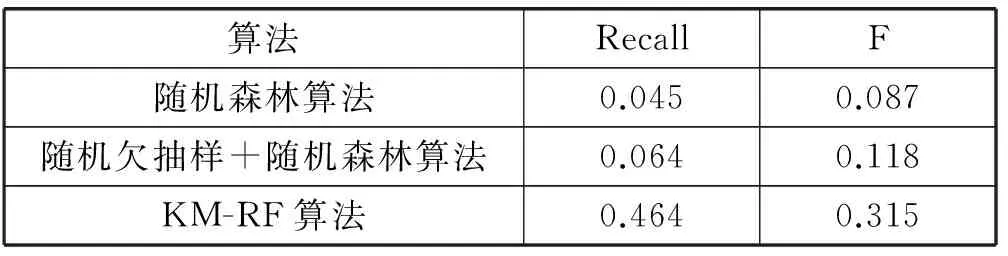
表6 三种算法Recall和F值对比

由该预测实验表明，KM-RF算法对比传统分类算法，在Recall和F值上均有显著的提高。

5 结 语

不平衡数据在实际应用中普遍存在，这使得对该类数据的研究成为数据挖掘领域的研究热点。本文根据k-means 聚类的特性，提出了基于k-means聚类的分类算法，并引入删除因子λ，降低欠抽样时丢失多数类数据的风险。实验表明，该算法具有较好的召回率和F值。最后本文将该算法应用于预测原发性肺癌术后一年期生存率，实验表明数据经k-means欠抽样处理后，分类算法的预测率具有显著的提升，也证明了该算法的实效性。

由于本实验在确定λ值时，根据多数类样本数目，多数类样本和少数类样本比，以及样本聚合程度等综合考虑，定性得出。另外当少数类样本较分散时，即聚类效果不明显时，算法分类较不明显。后续研究将重点放在如何定量确定λ值及其范围，使算法分类性能进一步优化。

[1] Ren F,Cao P,Li W,et al.Ensemble based adaptive over-sampling method for imbalanced data learning in computer aided detection of microaneurysm[J].Computerized Medical Imaging & Graphics the Official Journal of the Computerized Medical Imaging Society,2017,55(1):54-67.

[2] Radivojac P,Korad U,Sivalingam K M,et al.Learning from class-imbalanced data in wireless sensor networks[C]//Conference:Conference:Vehicular Technology Conference,2003.VTC 2003-Fall.2003 IEEE 58th,Volume:5.IEEE Xplore,2003:3030-3034.

[3] Fawcett T.“In vivo” spam filtering:a challenge problem for KDD[J].Acm Sigkdd Explorations Newsletter,2003,5(2):140-148.

[4] 李勇,刘战东,张海军.不平衡数据的集成分类算法综述[J].计算机应用研究,2014,31(5):1287-1291.

[5] Zhang X,Song Q,Wang G,et al.A dissimilarity-based imbalance data classification algorithm[J].Applied Intelligence,2015,42(3):544-565.

[6] Elkan C.The Foundations of Cost-Sensitive Learning[C]//Seventeenth International Joint Conference on Artificial Intelligence.2001:973-978.

[7] Chawla N V,Bowyer K W,Hall L O,et al.SMOTE:synthetic minority over-sampling technique[J].Journal of Artificial Intelligence Research,2002,16(1):321-357.

[8] 张枭山,罗强.一种基于聚类融合欠抽样的不平衡数据分类方法[J].计算机科学,2015,42(S2):63-66.

[9] Sun Z,Song Q,Zhu X,et al.A novel ensemble method for classifying imbalanced data[J].Pattern Recognition,2015,48(5):1623-1637.

[10] Weiss G M.Mining with rarity[J].Acm Sigkdd Explorations Newsletter,2004,6(1).

[11] Weiss G M.Mining with rarity:a unifying framework[J].Acm Sigkdd Explorations Newsletter,2004,6(1):7-19.

[12] Weiss G M,Hirsh H.A Quantitative Study of Small Disjuncts[C]//Seventeenth National Conference on Artificial Intelligence and Twelfth Conference on Innovative Applications of Artificial Intelligence.AAAI Press,1970:665-670.

[13] Provost F,Fawcett T.Robust Classification for Imprecise Environments[J].Machine Learning,2001,42(3):203-231.

[14] Ng W W Y,Zeng G,Zhang J,et al.Dual autoencoders features for imbalance classification problem[J].Pattern Recognition,2016,60:875-889.

[15] 刘学,张素伟.基于二次随机森林的不平衡数据分类算法[J].软件,2016,37(7):75-79.

[16] 胡晓星,李辉.胸外科肿瘤患者术前医疗风险评估表在病案中的应用[J].中国病案,2014(11):15-17.

[17] 王丹丹,陈情,毕平.肺癌左全肺切除术后心肺并发症的发生与术前低肺功能的相关性[J].中国肿瘤临床,2015,42(7):397-400.

[18] Zieba M,Tomczak J M,Lubicz M,et al.Boosted SVM for extracting rules from imbalanced data in application to prediction of the post-operative life expectancy in the lung cancer patients[J].Applied Soft Computing,2014,14(1):99-108.