聚类HMM模型在QAR数据分析中的应用研究

杨 慧 毛好好 霍纬纲

(中国民航大学计算机科学与技术学院 天津 300300)

0 引 言

QAR是飞机标准配置组件，真实地记录了飞行过程中的各种参数。随着民航运输业整体规模的扩大, 航空安全更加引人关注。近年来随着技术的不断进步，以QAR为代表的飞行数据记录设备不断更新升级，数据采集数量与质量都有很大提高，日益引起各航空运营商的高度重视[1]。针对QAR数据的研究，目前常用的方法是序列相似性匹配、小波变换、决策树以及关联规则等。如之前所做的QAR数据多维子序列的相似性搜索，基于 FP-Tree 的 QAR 数据故障检测研究等。但是这些方法主要关注在异常数据的检测与诊断，而忽略了故障或异常发生前后的状态。

隐马尔可夫模型(HMM)作为动态时间序列统计模型，具有严谨的数据结构和可靠的计算性能，早期成为语音识别的主流技术[2]。近几十年来， 隐马尔科夫模型被广泛地应用于各领域中，比如语音识别、行为识别、 生物学、 控制和经济领域等。黄晓彬等[3]对中国股市进行信息探测， 使用贝叶斯和马尔科夫链蒙特卡洛的方法，验证了该模型对市场信息的识别能力较强。随着研究的深入，国内外已开始把 HMM 方法引入到状态监测和故障诊断领域[4]。于天剑等[5]的HMM在电机轴承上的故障诊断，利用HMM方法与ANFIS方法相结合的情况来对故障问题进行建模，在频域内提取特征值，用ACC算法进行故障分类、最后用隐马尔可夫模型方法进行了故障预测。柳姣姣等的基于隐马尔科夫模型的时空序列预测方法[6]，提出了基于时空密度聚类的隐马尔科夫模型。本文提出一种基于聚类的HMM模型，针对QAR数据特点，分析发生故障或异常时QAR数据中不同属性的变化特点，提取主要影响属性进行分析。通过对其聚类进行数据离散化，并将其分为多个状态，对故障或异常发生的过程进行HMM建模。以状态序列的形式描述故障或异常发生的过程，以飞机空中颠簸故障为例，建立空中颠簸故障HMM模型，并检验了该模型的有效性。

1 相关工作

1.1 QAR数据

本文的目标是分析QAR数据，由于QAR数据是从传感器获取的流数据，其采样频率一般为每秒采样一次，数据量非常巨大。

QAR数据存在着以下几个特点：(1) 数据量巨大；(2) 时间性很强；(3) 参数种类众多；(4) 干扰多，随机性强，具有很多的不确定因素；(5) 需要很强的经验知识。

1.2 隐马尔可夫模型(HMM)

一个HMM即为五元组λ={N,M,A,B,π}，N为模型状态数，M为观察状态数。为了简便，常记为三元组λ={A,B,π}来表示一个隐马尔可夫模型。

隐马尔可夫模型(HMM)通常解决三个基本问题，针对三个问题并提出相对应的解决算法：

问题一：评估问题，即某个模型下观察值序列的概率计算问题。

问题二：解码问题，即隐马尔可夫模型的最优状态序列问题。

问题三：学习问题，即隐马尔可夫模型各种参数的训练问题。

HMM能够对非平稳信号变化的规律进行统计并建立参数化模型。QAR为时序数据，在飞机从正常到发生故障的过程中, 每个阶段的QAR数据在不断地发生变化。若对QAR的这些观测数据进行处理，通过学习训练出λ={A,B,π}，用 HMM来统计性地描述这些QAR数据的改变,以状态序列的形式描述故障的演化过程，并通过解码，得到最优的状态趋势序列，可以更好地识别飞机的状态趋势。

以空中颠簸故障为例，空中颠簸是威胁飞行安全的故障之一，而且空中颠簸的发生具有随机性，每次颠簸的强度也具有随机性。空中颠簸影响QAR数据不断发生变化，若把空中颠簸数据的状态趋势分成三个等级：严重颠簸、轻微颠簸和正常。由于空中颠簸故障发生在飞机飞行途中，地面人员无法直接得知颠簸程度，故可将空中颠簸故障发生时的状态趋势作为隐马尔可夫模型的隐状态。空中颠簸故障发生时，QAR数据的多个属性值受到影响而发生异常，QAR数据是可以直接观测到的。故可以作为隐马尔可夫模型的观测值，通过分析QAR数据，也就是分析观测值，训练得出隐马尔可夫模型参数，即隐马尔可夫模型的学习问题。状态转换如图1所示。

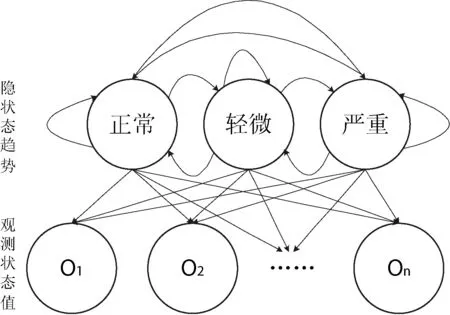
图1 状态转换图

训练得到空中颠簸故障的隐马尔可夫模型参数后，给定一个新的QAR时间序列，即可推测序列中数据所对应的最优的空中颠簸状态趋势，进行状态趋势分析，即隐马尔可夫模型的解码问题。但是由上面对QAR数据特点可知，QAR数据是高维数据，数据量大，且不同属性的数据类型也不相同，同一属性的观测值繁多。而隐马尔可夫模型的观测值的状态是有限的，故现在面临的问题是如何对QAR进行处理，使其符合隐马尔可夫模型中对观测值的要求。

2 基于聚类的HMM模型介绍

通过以上分析可知，由于QAR数据具有高维度、数据量庞大和数据复杂等特点，想要建立空中颠簸故障的隐马尔可夫模型，需对QAR数据进行处理，使其离散化为有限个状态值，从而符合隐马尔可夫模型对观测值的要求。本文选择用聚类算法对其QAR数据进行处理，但是直接对原始数据聚类，效率太低，在聚类之前先对QAR数据进行分段线性表示。然后利用改进的广度优先邻居搜索聚类算法对QAR数据进行聚类，根据聚类结果对数据进行离散化。最后利用训练数据得到隐马尔科夫模型参数。

2.1 基于固定分段数的自底向上分段算法

分段线性表示有数据压缩和过滤的作用。时间序列的线性分段表示方法很多，各类时间序列的特征不同，因此，分段表示及分析的方法也就不同。其次，我们对各类时间序列分析的目的也不相同，针对QAR数据的分析，因为正常情况的时间序列是平稳波动、有规律的，但发生异常或故障时就会出现突然的、零星的尖峰，这些异常则是我们关注的重点。针对众多时间序列的分段线性算法，选择合适QAR数据的分段算法，才能更好表示数据。选择合适的时间序列分段表示方法，不仅可以压缩飞行参数的数据量，同时还可以有效剔除原始参数序列中的噪声干扰。

廖俊等[7]提出的基于趋势转折点的分段线性表示，是只通过计算某个数据与前后两个数据的差值或距离来判断趋势点或特征点，都是局部算法，其精度和压缩比都不能很好地平衡。

如图2所示，在第400数据点附近，当出现一段数据连续上升或连续下降，且每次上升和下降的幅度较小时，存在的转折点或特征点无法识别，故不适合QAR数据。

图2 基于特征点的分段线性表示

自底向上分段算法，设置拟合误差阈值α，首先将将N个待分段的时间序列数据点两两连接 ,划分成不重合的N/2个初始分段即划分为相邻点的短序列，此时的拟合误差为0。然后将相邻两个短序列连接起来成为一个较长序列 ,再次计算中间所有点的拟合误差，找到误差最小且小于阈值α的分段即为第二个分段。依此方式循环，从中选择拟合代价最小的 ,如果该最小值小于分段阈值α, 则合并对应的两个相邻段, 直到所有分段的拟合误差都小于阈值α，分段完成。

但是自底向上算法进行分段时，设定误差阈值，虽然可以保证分段的精确度，但是所得的分段数无法确定，不利于进一步的分析。故本文借鉴固定分段数的思想，提出基于固定分段数的自底向上(BU)线性分段算法。

算法的主要思想:设置最大分段数N，拟合误差阈值e，进行自底向上的线性分段时，依次遍历，分别计算两点中间的所有点与该两点之间的最小二乘拟合线段的误差平方和，找到误差平方和最小且小于误差阈值e的线段，即为新的一个分段，用M记录已经得到的分段数，当M大于N时，停止分段。这样既保证了分段精度，也避免了由于精度值设置太大出现太多分段的现象，而且还可以根据实际情况的需要来确定分段数目。

拟合误差的平方和公式为：

Err=∑(y-y′)2

(1)

式中：y和y′分别表示两个分段点之间在同一时间点tc上的原始时间序列值和拟合值。其中拟合值是在两个分段点连接起来的线段上tc时刻对应的值，计算公式如下(其中k代表线段的斜率)：

k=(y1-y2)/(t1-t2)

(2)

y′=y1-k×t1+k×tc

(3)

在QAR数据中，参数众多，下面主要以06AccelVert属性的数据作为实验数据，具体说明实验结果。对数据进行预处理，提取所需要的巡航阶段QAR数据。采用上文提到的基于固定分段数的自底向上线性分段算法对1 000条飞机巡航阶段数据进行线性分段。规定分段的拟合误差阈值为0.5，分段数为20，分段数达到20时，停止分段。

图3中x轴表示时间，y轴表示当前时间的飞机06AccelVert属性的取值。

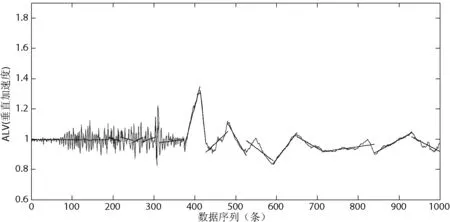
图3 基于固定分段数的BU分段结果图(长度1 000)

时间序列分段后，需要选择合适的模式来表示数据，不同的表示方式对后面的聚类也会有所影响。在大多数的线性分段算法方法中，常用线段平均值描述线段，也有其他的描述方法。章登义等[9]用斜率和长度描述线段。基于重要点的飞机发动机数据异常子序列检测[9]中则是用中值描述线段。针对QAR数据，分别用对两种表示方法进行分析。这两种方法描述QAR数据都有一定的局限。

第一，QAR数据正常时波动不大，波动较大时也不会超过0.4，因此会出现很多斜率很接近，但长度相差较大的线段所表示的状态是相同的。而针对线段斜率和长度进行聚类时，由于长度差异较大，这些状态相同的线段无法聚到一个类中。

第二，QAR数据异常时，数据波动较大，线段端点值较正常值差别很大，当用线段中点值来表示数据时，端点值被抵消，严重降低了异常数据与正常数据的差别。

根据以上的分析，使用线段的斜率和长度，或者斜率与中值都无法很好地表示线段。故本文针对QAR数据的特点对线段的表示方法进行改进，采用线段的斜率和线段端点值差的绝对值来表示。

图4中x轴是分段后所的线段的序列，一共20条线段，y轴是线段的值，其中虚线表示线段的斜率，实线表示线段的两端点的差的绝对值。可以看出，斜率变化较大的线段两端差的绝对值也较大，斜率变化小的线段两端差的绝对值小，该方法能很好地表示数据，更利于线段的聚类。

图4 所得分段的斜率和端点差的绝对值

2.2 二次广度优先邻居搜索聚类

广度优先邻居搜索聚类[10]即广度优先搜索某对象的直接邻居和间接邻居,将找到符合条件的所有邻居合并聚成一类。接着重复该步骤完成所有对象的聚类。

算法的基本思路是从待聚类的对象中的任意对象开始,基于广度优先和距离参数r,依次搜索该对象的直接邻居和间接邻居,对找到的每一个对象进行评估。如果符合设定的参数θ标准 ,则将它们聚为一类。接着重复该步骤直到所有对象都已聚类完毕。

广度优先邻居搜索聚类存在一定的局限性，因为采用相似矩阵表示对象之间的相似性，当数据量太大时，算法效率降低。QAR数据是时序数据，数据量巨大，针对这一局限性，对广度优先邻居搜索聚类进行改进以更好地适用于QAR数据。

QAR数据为流数据，即时序数据。关于时序数据的聚类，倪巍伟等[11]曾提出一种基于分区的思想，即首先按照时间顺序对数据进行分区，然后对分区中的数据进行聚类。本文对广度优先邻居搜索聚类的算法进行改进时，借鉴了分区的思想。即将QAR数据划分为数据块，每个数据块包含相同数目的数据点，分别对每个区块内的QAR数据进行广度优先邻居搜索聚类。得到每个区块内的聚类结果后，计算聚类中心，再对所得的聚类结果进行广度优先邻居搜索聚类，合并相似度高的类，得到最终的聚类结果。即二次广度优先邻居搜索聚类。

定义1设QAR时序数据X(X1,X2,…,XN)长度为N，数据划分长度为S，则数据被划分成M块。M=N/S。

用上文中提出的基于固定分段数的自底向上分段算法对每个区块内的数据进行分段。

定义2设某区块的分段数为c，用线段斜率和端点差的绝对值表示数据，数据表示为((k1,d1),(k2,d2),…,(kc,dc))。

飞机发生故障时表现为QAR数据波动异常，异常点往往是孤立点或者离群点，与同类算法相比, 改进的广度优先搜索聚类算法具有实现简单、复杂度低和容易设定最佳参数等优点, 并且能够很好地识别孤立点,发现任意形状的聚类。就QAR数据特点而言，该算法合适对QAR数据进行聚类。

QAR数据是一种时序序列，针对时间序列的数据挖掘，通常要将数据点密集的长时间的序列转换成相对稀疏的具有特定意义的符号序列，即转化为相对简单且易于分析处理的形式[12]。采用二次广度优先邻居搜索聚类算法对序列进行聚类，分析聚类结果，给每类赋予相应的类别标签，并用类标签代替原始数值序列，实现数据离散化。为隐马尔科夫模型的建立做准备。

2.3 模型建立

QAR数据的隐马尔可夫模型的模型建立大致分为以下三个阶段：第一阶段，线性分段，对QAR数据进行压缩；第二阶段：聚类，得到聚类结果，分析聚类结果，实现数据符号化，得到观测状态；第三阶段：使用前向后向算法训练数据建立HMM模型。

具体实现步骤如下：

步骤1进行QAR数据预处理，得到最初的原始数据，并将其分为训练数据和测试数据。

步骤2对所有数据用基于固定分段数的自底向上分段算法进行线性分段表示。

步骤3对分段后所得线段用二次广度优先邻居聚类算法进行聚类，得到结果，分析聚类结果，实现数据符号化，得到观测状态，将数据序列都转化为有限个观测态的序列。

步骤4用MATLAB中estimate方法初始化模型参数λ0。

步骤5训练数据的序列作为离散隐马尔科夫的观测序列，用EM算法训练隐马尔科夫模型参数，即隐马尔可夫模型的学习问题，获得最优模型λ。

3 实 验

实验工具选用MATLAB R2010a，实验平台配置为2.13 GHz的CPU、6 GB内存的PC，操作系统为Windows 7，实验数据某B737型飞机记录的数据。

3.1 QAR数据预处理

本文的QAR数据，来自于已经过QAR译码的CSV文件。CSV文件的QAR数据是已经过译码后的工程值文件。 通过对CSV文件的研究可知，飞机发生的许多故障通常和一部分QAR数据属性相关，因此可以从发生的故障类型和发生故障的机型着手，去查看QAR数据CSV文件中的相关属性列，并选取某些属性和某些故障作针对性的研究。空中颠簸故障相关的属性主要有EPR(发动机压比)、EGT(排气温度)、ALV(垂直加速度)、VIB(振动)、N1(低压转子转速)和N2(高压转子转速)。按照层次分析法，专家对空中颠簸故障发生相关属性重要程度进行了统计和调查。根据专家经验可得飞机在空中是否有空中颠簸的故障发生主要与飞机的垂直加速度的属性值有关，故本文只提取垂直加速度ALV数据来分析空中颠簸故障。数据预处理后得到飞机巡航阶段的垂直加速度(ALV)数据，用其中 57 576条数据作为训练数据。

3.2 QAR数据分析

运用改进的广度优先邻居搜索聚类算法对数据聚类。首先对训练数据进行分区，这里取每个区长度分别为S=1 000，对每个数据区进行基于固定分段数的自底向上线性分段，并用每个线段的斜率和端点值差的绝对值表示线段，即此时每条线段可用二维上的点来表示。下面以某个区为代表进行说明，图5为57区数据，图6为第57区的聚类结果。

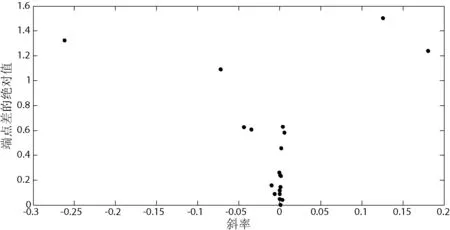
图5 第57区的线段

图6 第57区线段聚类结果

每个分区聚类结束后都要计算并记录下每一类的聚类中心，聚类中心即为每类中线段的平均值，存储在新的数据文件中。用分区聚类结束后，所有类的聚类中心在同一个数据文件中。针对这些聚类中心进行二次聚类，即并合并相似度高的类，聚类结果如图7所示。

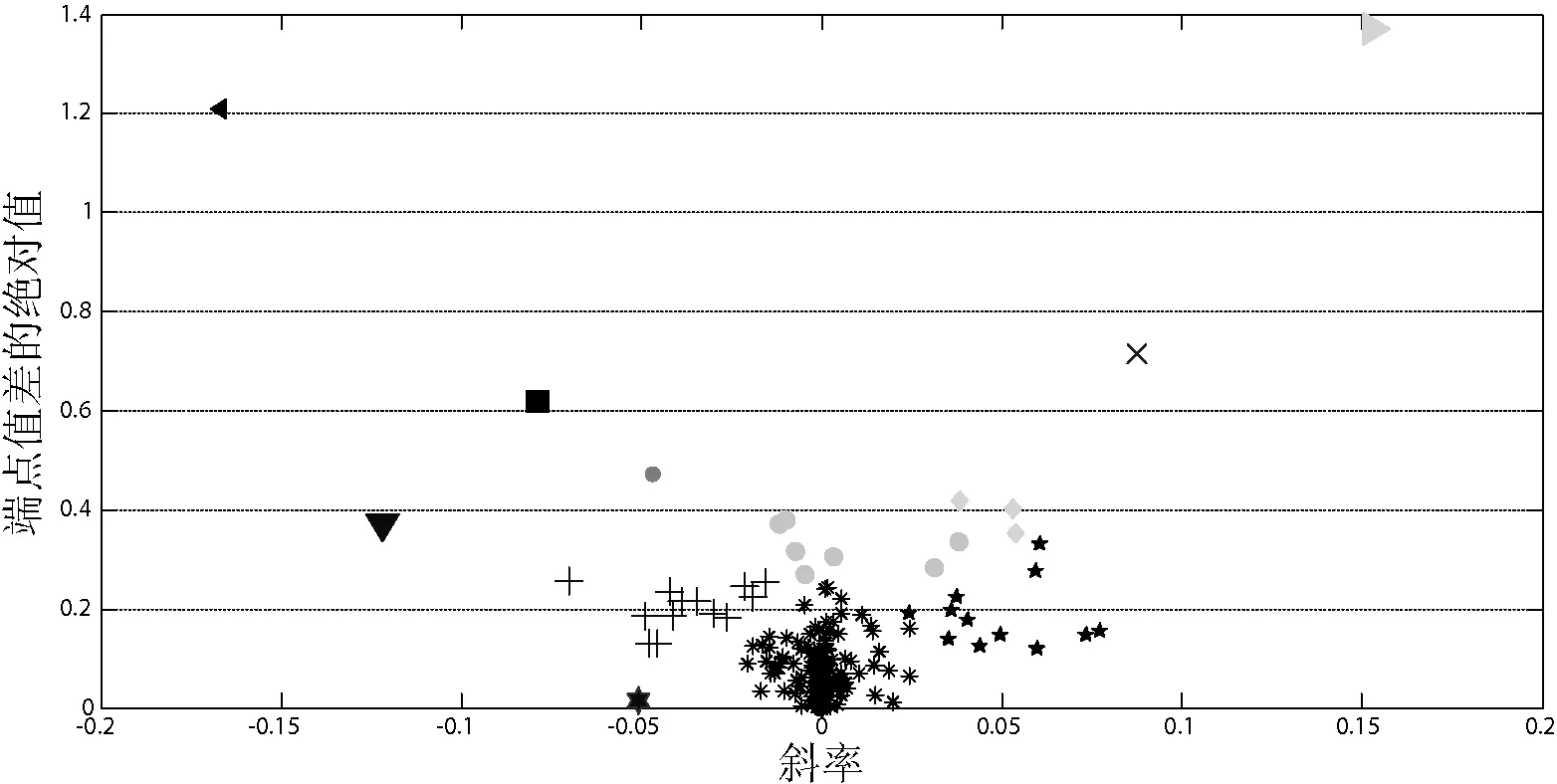
图7 对区块类的聚类中心的聚类结果

对聚类结果进行分析，图7中斜率接近0的线段，线段的端点值差的绝对值也小，这样的线段被聚为一类，这类数据几乎没有变化，即数据趋势为平稳；图7中斜率小于0，且端点差的绝对值在0.2附近的线段被聚为一类，这些数据趋势为轻微下降；同样图7中斜率大于0，且端点差的绝对值在0.2附近的哪一类线段的数据趋势为轻微上升；斜率小于0，且端点差绝对值变化较大的数据，其数据趋势为突然下降；同理，斜率大于0，且端点差绝对值变化较大的数据，其数据趋势为突然上升。

对所得聚类结果进行统计，根据以上分析、汇总可得到训练数据的趋势情况，汇成表格结果见表1。

表1 线段趋势情况

通过以上对聚类结果的分析与统计，采用效果最合适的聚类对其数据进行符号化，用5种趋势的标签代替原始数据的值作为离散隐马尔科夫的观测序列。故此时隐马尔科夫的观测状态共有5种，即平稳、轻微上升、轻微下降、突然上升和突然下降。分别用0、1、-1、2、-2表示。图8为训练数据的线段的趋势。

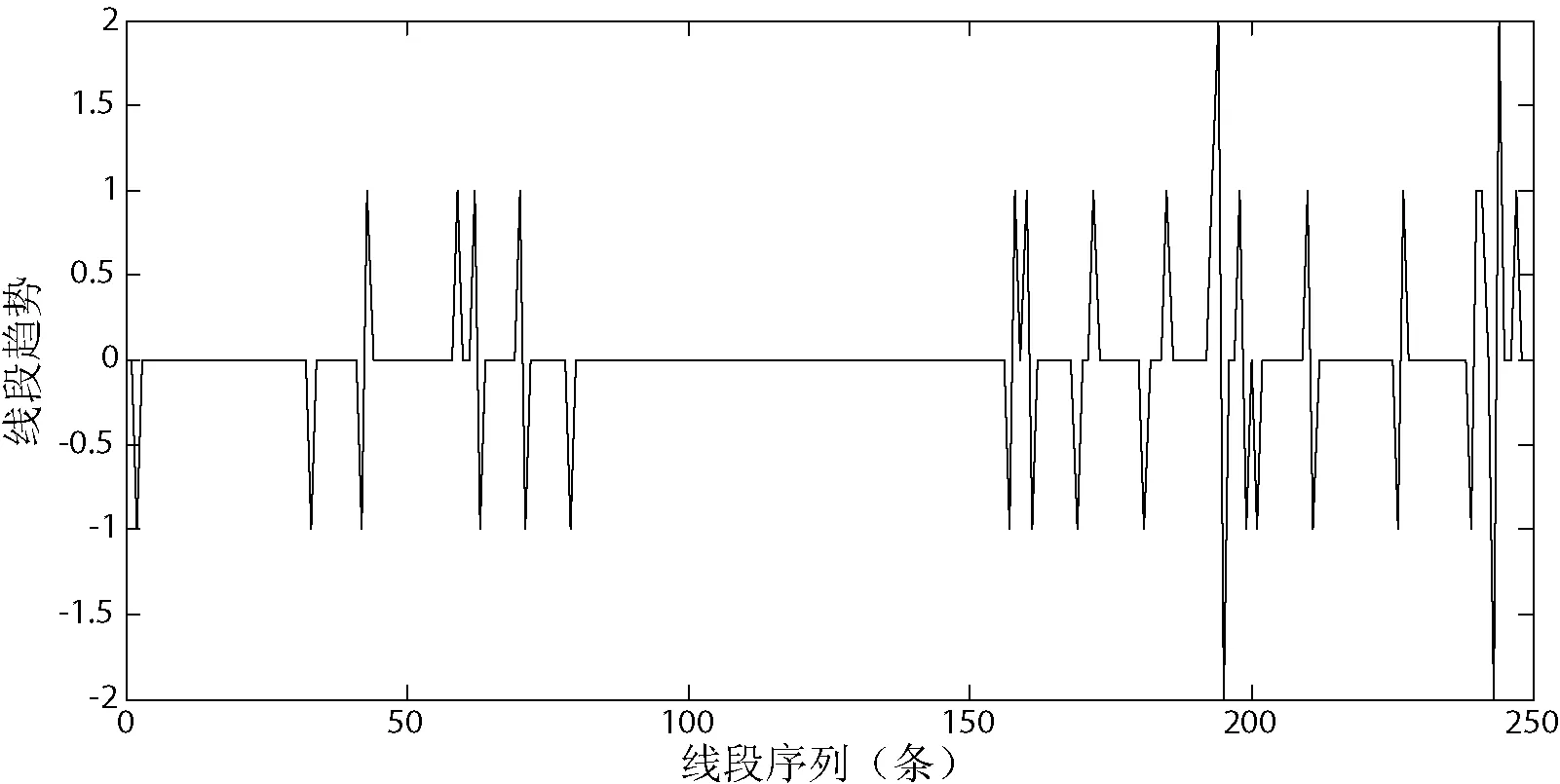
图8 线段趋势图

由分析可知，飞机发生空中颠簸故障时，主要影响到的是飞机垂直加速度(ALV)的属性值。故将飞机的运行状态作为隐马尔科夫的隐状态，即设定隐马尔可夫模型的隐状态有三种，分别是正常、轻微颠簸和严重颠簸，用数值1、2、3表示。根据聚类中心值可初步确定观测序列所对应的初始的状态序列。在已知观测序列和预设状态序列的情况下，可用MATLAB中的hmmestimate方法估计状态转移概率矩阵和发射概率矩阵。将此作为EM算法的初始值。

根据得出的观测序列及与其对应的状态序列估计其状态转移概率矩阵和发射概率矩阵，并采用前向后向算法得出训练后的状态转移概率矩阵和发射概率矩阵。分别如下：

训练前：

训练后：

用训练所得HMM模型预测测试数据中飞机的运行状态。数据同样来自某 B737型飞机记录的并经过数据预处理后得到的飞机巡航阶段的垂直加速度(ALV)数据，从中提取四组数据，分别是2 000条、2 000条、5 000条、5 000条。首先对四组测试数据结合之前的聚类方法，运用k-近邻算法得出其分类标签，完成数据的符号化，即用线段的趋势来表示符号化数据。然后采用Viterbi算法预测其状态。

下面为测试数据中不同的两段数据的预测情况对比。图9为数据1中某段原始数据，图10为该段数据的预测结果。

图9 数据1中某段原始数据

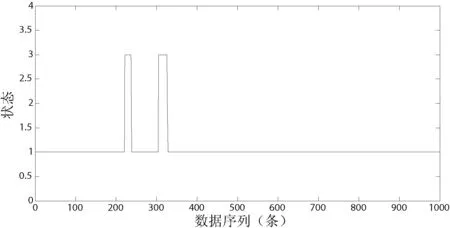
图10 数据1中某段预测结果

图9为原始序列图，横坐标为数据序列号，纵坐标为垂直加速度属性值。图10是预测结果图，其中横坐标还是数据序列号，纵坐标为飞机运行状态。从中可以看出，在飞机出现空中颠簸时，垂直加速度数据异常，该模型能够预测出异常数据，并判断其颠簸的程度。图10识别出了两段严重颠簸状态。

四组数据的具体预测结果如表2所示。

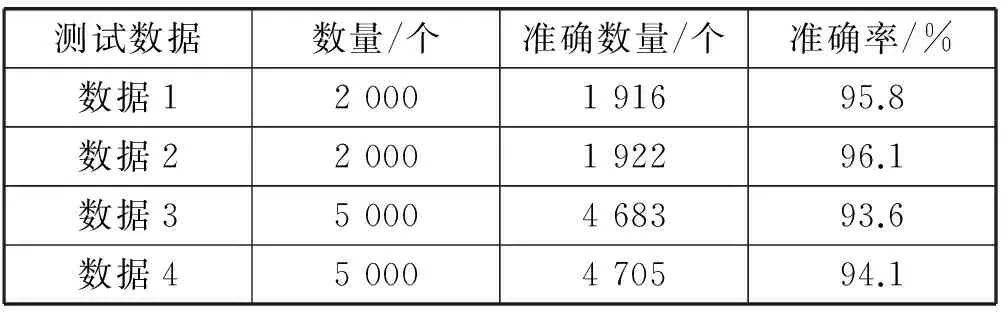
表2 预测情况统计

通过以上大量的测试实验，该模型能很好地预测原数据的状态趋势。但是当需要识别的数据长度增加时，其预测精度有所降低，但大部分的状态能够预测。可知通过对QAR的数据进行趋势分析，以平稳、轻微上升、轻微下降、突然上升和突然下降这5种趋势来表示QAR数据，将QAR数据转化为有限个观测值，作为隐马尔可夫模型的观测序列。经过学习训练建立的隐马尔可夫模型能很好地预测空中颠簸数据的状态趋势。虽然该模型目前能够预测出颠簸状态，但是飞机出现空中颠簸是不确定性的，因此需要大量的监控历史数据来不断训练学习，才能保证更加精确地预测飞机的运行状态。

4 结 语

本文针对传统的QAR数据分析方法只关注异常点而忽略了QAR的状态趋势特征的问题。通过分析QAR数据与飞机空中颠簸故障，针对大量QAR数据，提出一种基于聚类的HMM模型，分析发生故障或异常时QAR数据中不同属性的变化特点。通过对聚类进行数据离散化得出数据的状态趋势，并用类标签代替原始数值序列，进行数据离散化，对飞机巡航阶段空颠簸故障数据进行了有效处理，建立了有效的HMM模型。用HMM来统计性地描述故障发生时QAR数据的改变,以状态序列的形式描述故障的演化过程，并能够根据观测数据有效识别飞机所处运行状态趋势，成功验证了该方法的有效性。

[1] 曹惠玲,周百政.QAR数据在航空发动机监控中的应用研究[J].中国民航大学学报,2010,28(3):15-19.

[2] Jiang H,Li X,Liu C.Large margin hidden Markov models for speech recognition[J].IEEE Transactions on Audio Speech & Language Processing,2005,14(5):1584-1595.

[3] 黄晓彬,王春峰,房振明,等.基于隐马尔科夫模型的中国股票信息探测[J].系统工程理论与实践,2012,32(4):713-720.

[4] 张璇,周峰.隐马尔科夫模型应用领域、热点及趋势分析——基于CiteSpaceII[J].现代商贸工业,2015,36(15):63-65.

[5] 于天剑,陈特放,陈雅婷,等.HMM在电机轴承上的故障诊断[J].哈尔滨工业大学学报,2016,48(2):184-188.

[6] 柳姣姣,禹素萍,吴波,等.基于隐马尔科夫模型的时空序列预测方法[J].微型机与应用,2016,35(1):74-76.

[7] 廖俊,于雷,罗寰,等.基于趋势转折点的时间序列分段线性表示[J].计算机工程与应用,2010,46(30):50-53.

[8] 章登义,欧阳黜霏,吴文李.针对时间序列多步预测的聚类隐马尔科夫模型[J].电子学报,2014(12):2359-2364.

[9] 杨慧,王光霞.基于重要点的飞机发动机异常子序列检测[J].计算机工程与设计,2016,37(9):2543-2547.

[10] 钱江波,董逸生.一种基于广度优先搜索邻居的聚类算法[J].东南大学学报(自然科学版),2004,34(1):109-112.

[11] 倪巍伟,陆介平,陈耿,等.基于k均值分区的数据流离群点检测算法[J].计算机研究与发展,2006,43(9):1639-1643.

[12] 任江涛,何武,印鉴,等.一种时间序列快速分段及符号化方法[J].计算机科学,2005,32(9):166-169.