罗氏线圈在变压器短路电流试验时的测量误差
王洪权 任晓明
摘要
罗氏线圈是一种通过感应方式测量回路电流的测量仪器,以其线性度好、安装便捷和质量轻等优点普遍应用于各种电流检测场合中。在变压器短路试验,有时测得结果是一个正弦波和非周期性衰减指数波叠加而成,对实际峰值和功率因素的计算造成较大误差,因此,本文通过Matlab仿真得出在积分时间超过10s情况下,有源外积分罗氏线圈可以满足功率因素大于0.15时的短路电流的测量要求。
【关键词】罗氏线圈 短路试验 Matlab仿真功率因素
在进行变压器短路试验、低压电器的分断试验时均需要测量输出的工频短路电流。当前工频短路电流的测量主要用电流互感器、霍尔传感器、分流器或罗氏线圈。与其他几种测量方式比较,罗氏线圈没有铁芯,不会产生磁饱和现象;通过感应方式测量电流,线圈和被测回路之间没有直接的电的联系;对被测回路的影响较小不会消耗被测回路的能量低成本、易于安装,可适应不同的安装位置,由于这些优点它越来越多地用于电力系统中短路电流测量。文献[3]分析了自积分式罗氏线圈在测量高变化率的电流比外积分式有更好的性能。文献[4]对有源外积分器罗氏线圈和无源外积分器罗氏线圈进行了比较分析,得出有源外积分电路在测量电力系统暂态信号方面有更好的性能。因此短路电流测量中大多使用的是外积分式罗氏线圈。采用这类线圈对工频短路电流进行测量的时候,由于短路电流的波形是周期性的正弦波叠加一个非周期性的衰减指数波,这导致测量得到的电流波形与实际的短路电流波形并不严格一致,在短路电流波形的起始部分尤为明显,线圈参数的选用不当会对峰值、有效值和功率因数的计算造成比较大的误差。文献[5]通过理论计算弥补罗氏线圈的性能,文献[6]通过延长时间常数提升线圈的性能来降低这个问题的影响。
本文通过仿真得出在下限频率为0.016Hz或积分时间常数大于10s的有源外积分罗氏线圈可以满足cosφ≥0.15短路电流的测量要求。
1 有源外积分罗氏线圈模型
罗氏线圈用于测量时,其感应电压与互感M和电流的变化率成比例:
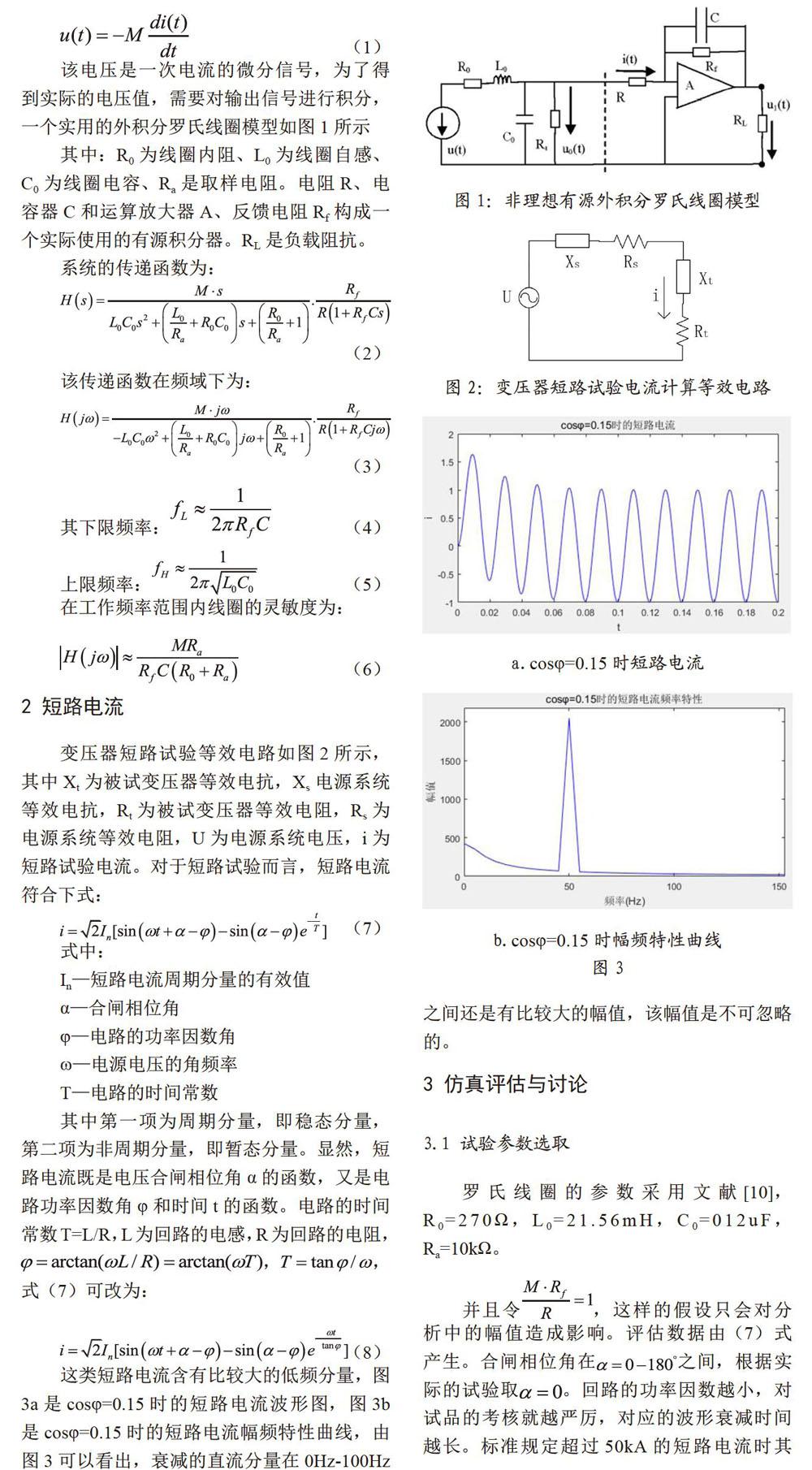
该电压是一次电流的微分信号,为了得到实际的电压值,需要對输出信号进行积分,一个实用的外积分罗氏线圈模型如图1所示
其中:R0为线圈内阻、L0为线圈自感、C0为线圈电容、Ra是取样电阻。电阻R、电容器C和运算放大器A、反馈电阻Rf构成一个实际使用的有源积分器。RL是负载阻抗。
系统的传递函数为:
该传递函数在频域下为:
其下限频率:
上限频率:
在工作频率范围内线圈的灵敏度为:
2 短路电流
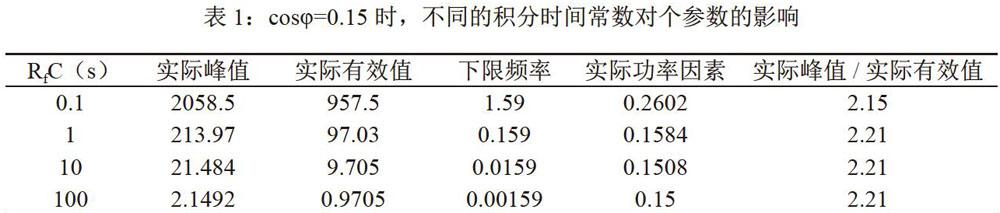
变压器短路试验等效电路如图2所示,其中Xt为被试变压器等效电抗,Xs电源系统等效电抗,Rt为被试变压器等效电阻,Rs为电源系统等效电阻,U为电源系统电压,i为短路试验电流。对于短路试验而言,短路电流符合下式:
式中:
Ln—短路电流周期分量的有效值
α—合闸相位角
φ—电路的功率因数角
ω—电源电压的角频率
T—电路的时间常数
其中第一项为周期分量,即稳态分量,第二项为非周期分量,即暂态分量。显然,短路电流既是电压合闸相位角α的函数,又是电路功率因数角φ和时间t的函数。电路的时间常数T=L/R,L为回路的电感,R为回路的电阻,φ=arctan(ωL/R)=arctan(ωT),T=tanφ/ω,式(7)可改为:
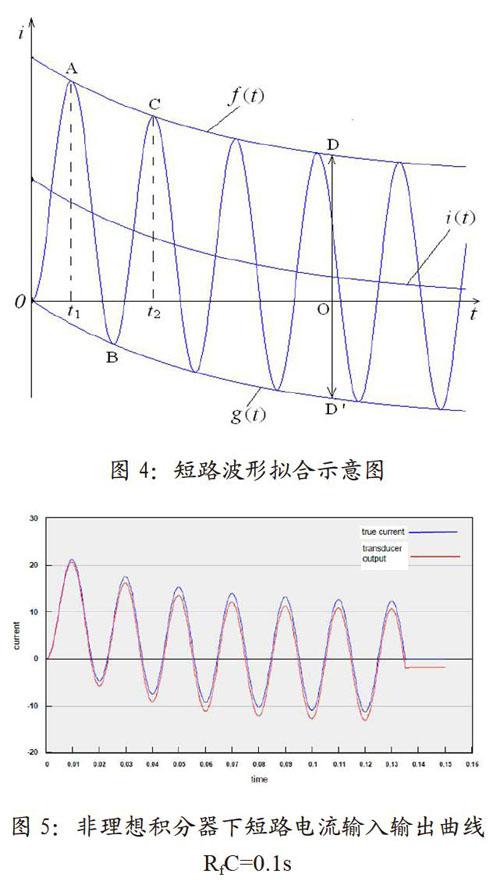
这类短路电流含有比较大的低频分量,图3a是cosφ=0.15时的短路电流波形图,图3b是cosφ=0.15时的短路电流幅频特性曲线,由图3可以看出,衰减的直流分量在0Hz-100Hz之间还是有比较大的幅值,该幅值是不可忽略的。
3 仿真评估与讨论
3.1 试验参数选取
罗氏线圈的参数采用文献[10],R0=270Ω,L0=21.56mH,C0=012uF,Ra=10kΩ。
并且令,这样的假设只会对分析中的幅值造成影响。评估数据由(7)式产生。合闸相位角在α=0-180°之间,根据实际的试验取α=0。回路的功率因数越小,对试品的考核就越严厉,对应的波形衰减时间越长。标准规定超过50kA的短路电流时其cosφ=0.2-0.050,因此取cosφ=0.15进行分析已经足够严格。令In=1000A,对(7)式离散化处理,短路电流波形持续时间为0.2秒,采样率为20480点/秒。
3.2 参数的计算原理
3.2.1 有效值的计算
先求出短路电流的峰点和谷点后,用双指数拟合的方法分别求出上、下包络线,如图4中的f(t)和B(t)"两者的算术平均值i(t)即为短路电流的直流分量。
求出A,B,C等峰值处的峰值后,即可得到各对应点的有效值和直流分量。如DD'处波形的有效值等于,所包含的直流分量等于。文中的有效值是采用A点计算出的有效值。
3.2.2 功率因数的计算
功率因数cosφ可根据非对称电流波形的直流分量曲线来确定。图4中,设点A,C分别是该电流波形的第一个与第二个电流峰点,其对应峰点时间为t1与t2,对应峰点时间的直流分量分别为id1与id2,则。将上述两式相除并变形可得:
则功率因数可表示为:
其中f为电源频率。
3.3 仿真与分析
图5显示的是一个理论波形和该理论波形通过RfC-0.1s罗氏线圈后测量得到的一个波形。两者波形有明显的差异,测量波形总体朝下偏移。在积分器非理想,其测量输出不可避免都会出现这种现象,这将对峰值、有效值、功率因数的计算造成影响。
偏移问题可以通过设计长时间常数模拟积分器,或者采用数字积分方式,或通过优化设计线圈来降低影响。短路的暂态过程持续时间约为几十ms,由式(5)可知,上限频率在不同的积分时间常数下几乎是相同的,均为3kHz附近,这已经可以测量到60次谐波了,因此上限频率对短路波形测量的影响可以不用考虑;但是下限频率对波形的影响是明显的。表1表示cosφ=0.15时,不同的积分时间常数R不,各理论计算值与测量值的误差。根据上文的参数,短路波形的理论峰值为2207A,有效值为996.7A,峰值/有效值=2.21。由表1可知,时间常数与测量峰值和有效值成反比,与下限频率成反比,峰值和有效值体现的是线圈灵敏度,对于cosφ=0.15的短路电流波形在RfC=10时,其峰值与有效值之比己和理论值一致,其功率因数己符合测量的要求。
4 结论
工频短路电流的测量通常采用有源外积分罗氏线圈,本文采用此线圈测量变压器短路电流。短路电流中包含一定的低频分量,甚至含有直流信号,低频分量的大小和回路的固有时间常数有很大的关系。积分器时间常数的变化对罗氏线圈的高频特性几乎没有影响,积分器的时间常数越大低频响应越好,但是此时需要付出灵敏度降低的代价。对于采用电磁感应原理进行电流测量的罗氏线圈而言,通过加大积分器的时间常数可以扩展低频段的性能,但是对于短路电流中的直流分量是無法测量。本文通过仿真得出下限频率小于0.016Hz,或积分时间常数大于10s的线圈均可以满足cosφ≥0.15短路电流的测量要求。
参考文献
[1]聂一雄,尹项根,张哲.磁位计在电力系统继电保护中应用的可行性探讨[J].电力系统自动化,2000,24(16):35-38.
[2]张涛,李澎,罗承沐等.罗果夫斯基线圈测量高电压及电力系统中的暂态电流[J].电工电能新技术,2002,21(03):53-56.
[3]李维波,毛承雄等.陡脉冲大电流的Rogowski测量线圈仿真研究[J].高电压技术,2002,28(08):11-13.
[4]许桂敏,刘全桢,刘宝全等.标准10/350μs雷电流波的频谱分析[J].电瓷避雷器,2010(05):45-47.
[5]王新新,吴泽辉.Rogowski线圈的波形畸变及其校正[J].高电压技术,1996,22(03):16-19.
[6]Wei Li,Xianggen Yin,Deshu Chen,Wei Chen,ZheZhang,andYongjun Xia.The Study of Transient Performanceof Current Sensor Based on RogowskiCoil and Its Application inDynamic Simulation Experiment[C].International Conference on PowerSystem Technology,Chongqing,China,2006.
[7]The Study of Transient Performanceof CurrentSensor Based on RogowskiCoil and ItsApplication in DynamicSimulation Experiment.
[8]Wei Li,Xianggen Yin,Deshu Chen,Wei Chen,ZheZhang,andYongjun Xia.The Study of Transient Performanceof Current Sensor Based on RogowskiCoil and Its Application inDynamic Simulation Experiment[C].International Conference on PowerSystem Technology,Chongqing,China,2006.
[9]贺以燕,杨治业等.变压器试验技术大全[M].辽宁:辽宁科学技术出版社,2006:230-231.
[10]刘艳峰,尚秋峰,周文昌.Rogowski线圈典型外积分电路暂态性能比较与仿真[J].电力自动化设备,2006,26(07):30-33.
[11]GB14048.1-2006表8和表16.
[12]高鹏,高明,吴成忠.浅析电流互感器拖尾电流对失灵保护的影响[J].华中电力,2012,25(01):7-9.

