分离参数法妙解恒成立问题

翟爱国

所谓分离参数，是指在含有参数的不等式中，通过恒等变形，使参数与主元分离于不等式两端，则所蕴涵的函数关系便由隐变显，从而问题可转化为求主元函数的值域（最值）进而求出参数范围.这种方法由于思路清晰、规律明显、操作性强，因而应是一种较好的求参方法.

一、不等式恒成立问题

对于不等式恒成立问题，常见的解法需把参数a分离出来，化成a≥f（x）或a≤f（x）恒成立的形式，则a≥f（x）恒成立⇔a≥f（x）max；a≤f（x）恒成立⇔a≤f（x）min.这样可转化为函数最值问题，进而求参数a的取值范围.

例1若不等式x2＋ax＋1≥0，对一切，求a的取值范围.

分析思路1，通过化归最值，直接求函数的最小值来解决，即

解法1设f（x）＝x2＋ax＋1，对一切恒成立，函数f（x）的对称轴

解法2原不等式等价于一切成立，设u＝则u在是减函数，故当时，u取到最小值

点评本题若采用构造函数法来解决问题，需要构造二次函数，利用二次函数的图象和性质进行分类讨论，讨论过程比较复杂；而本题若采用分离参数法，所求参数a是很容易分离出来的，再转化成求函数（对勾函数）上的最小值问题，这样处理相对来说简单点.同学们好好体会用分离参数法解恒成立问题的妙处.

例2已知x∈（-∞，1]时，不等式1＋2x＋（a-a2）·4x＞0恒成立，求a的取值范围.

解析令2x＝t，因为x∈（-∞，1]，故t∈（0，2]，所以原不等式可化为要使上式在t∈（0，2]上恒成立，只须求出在t∈（0，2]上的最小值即可.

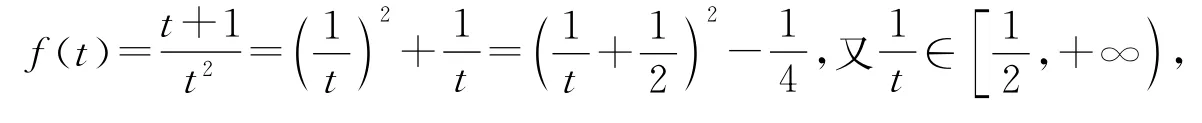
点评在给出的不等式中，如果通过恒等变形不能直接解出参数，则可将两变量分别置于不等式的两边，即若f（a）≥g（x）恒成立，只须求出g（x）max，则f（a）≥g（x）max，然后解不等式求出参数a的取值范围；若f（a）≤g（x）恒成立，只须求出g（x）min，则f（a）≤g（x）min，然后解不等式求出参数a的取值范围，问题还是转化为函数求最值.

例3设其中a∈R，如果当x∈（-∞，1]时，f（x）有意义，求a的取值范围.

分析当x∈（-∞，1]时，f（x）有意义⇔当x∈（-∞，1]时恒 成立.

解令当x∈（-∞，1]时，只需a＞f（x）max.

点评对于一些看似非不等式恒成立问题（如定义域、单调性问题等），可通过等价转化的方法转化为不等式恒成立问题来处理.

二、方程恒有解问题

若已知含参数的方程恒有解（不涉及解的个数），可把参数分离于方程一端，通过求函数的值域，求得参数的取值范围.

例4关于x的方程9x＋（4＋a）3x＋4＝0恒有解，求a的范围.

分析本题中出现了3x及9x，故可通过换元转化成二次函数型求解.

解设3x＝t，t＞0，则原方程有解即方程t2＋（4＋a）t＋4＝0有正根.

当且仅当t＝2时“＝ ”号成立，因此a≤-8.

点评利用分离参数法解方程恒有解问题，这样做思路清楚，解法简洁，同学们若掌握这种转化思想，可使此类问题得以顺利解决.

三、参变量转换问题

数学中的未知数与参变量之间没有绝对的区别，即角色可以互换.处理此类问题，打破常规，恰当地选择未知数做主元是解题的关键，往往会取得出奇制胜的效果.

例5对于满足0≤p≤4的一切实数，不等式x2＋px＞4x＋p-3恒成立，试求x的取值范围.

分析习惯上把x当作自变量，记函数y＝x2＋（p-4）x＋3-p，于是问题转化为：当p∈[0，4]时，y＞0恒成立，求x的取值范围.解决这个等价的问题，容易因计算繁琐出错或者中途夭折.如果把变元与参数换个位置，构造成关于参数的一次函数，本题迎刃而解.

解设函数f（p）＝（x-1）p＋（x2-4x＋3），显然x≠1，则f（p）是p的一次函数，要使f（p）＞0恒成立，当且仅当f（p）min＞0，即f（0）＞0，且f（4）＞0.解得x的取值范围是（-∞，-1）∪（3，＋∞）.

点评本题看上去是一个不等式问题，但是经过等价转化，把它化归为关于p的一次函数，利用一次函数的单调性求解，解题的关键是转换变量角色.一般来说，可将已知存在范围的量视为变量，而待求范围的量视为参数.

上面和同学们分享了解决恒成立问题的一种重要方法——分离参数法，将恒成立问题转化为函数的最值（值域）问题.在具体的解题实践中，方法有很多，往往需要我们综合考虑，灵活运用，才能使问题得以顺利解决.

巩固练习

1.已知函数f（x）＝-x2＋2x-3a，当-1≤x≤2时，恒有-3≤f（x）≤2，则实数a的取值范围是________.

2.已知函数f（x）＝4x-（k＋1）·2x＋2，若f（x）＞0恒成立，则k的取值范围是________.

参考答案