基于EMF的面装式永磁同步电动机无速度传感器的Simulink仿真

高辉，杨涛

摘 要：永磁同步电动机结构较为简单，易于控制。传统方法是在转子上安装编码器以获得位置与速度信息来实现调速，但永磁同步电动机转子安装编码器有许多缺点，诸如系统的鲁棒性会降低，高精度编码器价格居高不下，有些恶劣条件下例如高粉尘的场合下甚至不能使用这类编码器。因此，寻找一种方法来替代编码器变得尤为迫切。文章运用坐标转换理论分析了永磁同步电动机的数学模型，在面装式同步电机模型的基础上，运用FOC的控制策略和SVPWM技术，研究了EMF（Electromotive Force）控制策略在Matlab2014a Simulink环境下的无速度传感器的FOC闭环控制。

关键词：EMF；永磁同步电动机；FOC无速度传感器控制；SPWM；Matlab Simulink

中图分类号：TM341 文献标志码：A 文章编号：2095-2945（2018）06-0015-03

Abstract： The structure of permanent magnet synchronous motor （PMSM） is simple and easy to control. The traditional method is to install encoders on the rotor to obtain the information of position and speed to achieve speed regulation， but the rotor encoder of PMSM has many disadvantages， for example， the robustness of the system will be reduced， the price of high precision encoders is so high， and they can't even be used in bad conditions with high dust. Therefore， it is urgent to find a way to replace the encoder. In this paper， therefore， the mathematical model of permanent magnet synchronous motor （PMSM） is analyzed by means of coordinate transformation theory. On the basis of the model of planar synchronous motor， and with the control strategy of FOC and SVPWM technology， EMF （Electromotive Force） is studied for the FOC closed-loop control of the without-velocity sensor in the environment of Matlab2014a Simulink.

Keywords： EMF； permanent magnet synchronous motor （PMSM）； without-velocity sensor control； SPWM； Matlab Simulink

引言

近年來，随着高性能永磁材料技术、电力电子技术的发展，以及矢量控制理论、自动控制理论研究的不断深入，永磁同步电机以其结构简单、运行可靠、体积小、重量轻、效率高、控制简单优点得到了迅速发展，目前在高性能、高精度等领域还有待提高[1-2]。通常交流电机控制系统由交流电机，逆变器，速度、位置传感器、速度、位置、电流控制器构成。在电机调速系统中，使用光电编码器来采集转速信息，因为采用机械装置会增加系统的成本，所以无速度传感器控制方案成为永磁同步电机研究的热点之一，问题本质是在去除编码器的情况下如何通过电机的信号（例如定子电压、电流）重新建立数学模型获得反馈所需的位置角与转子转速[3-4]。本文基于矢量控制理论，利用扩展反电动势法建立其数学模型，应用Matlab Simulink软件构建控制系统并进行分析。

1 永磁同步电机的数学模型

永磁同步电动机在三相固定坐标系（abc）下的磁链方程（1）、电压方程（2）、转矩方程（3）为：

ia，ib，ic：abc三相绕组电流；？鬃a，？鬃b，？鬃c：三相坐标系下的磁链；？鬃f：转子永磁体产生的励磁磁链；LAA，LBB，LCC：永磁同步电动机三相绕组自感；？棕e：PMSM中的电气角速度；？兹e：PMSM中d轴超前a轴的电角度；ua，ub，uc：abc三相绕组电压；Rs：永磁同步电动机定子侧绕组电阻；p：微分算子（=d/dt）；Te：电磁转矩；pn：极对数。

Clerk坐标变换理论实现了三相静态坐标系u、v、w到两相固定坐标系？琢-？茁的转换，变化后的磁链方程（4）、电压方程（5）、转矩方程为（6）Park坐标变换理论实现了两相固定坐标系到两相旋转坐标系d-p的转化。变化后的磁链方程（7）、电压方程（8）、转矩方程为（9）：

对比三相固定坐标参考系、两相固定坐标参考系，两相旋转坐标参考坐标系的永磁同步电动机数学模型最为简便。

2 永磁同步电动机的无速度传感器技术

在本节主要研究对于面装式永磁同步电动机的扩展反电动势（Back EMF）的无速度传感器控制方法。

通过以上（4）、（5）数学模型并转到旋转坐标系能得到转速与位置信号的关系式（10）。

不难看出如果可以将电机转子转速ωe和转子位置θe提取出来，那么永磁同步电动机的无速度传感器转速控制将会成为可能。为此，在d-q轴的预估轴？酌-？啄上我们可以将上式改写为：

如此式（11）用来预测转子位置。

由扩展反电动势法，转子的位置公式为：

（13）

结合式（12），整理得出：

其中，？兹e？艿■e

一旦得到电动机的位置角信号后，对其微分可得到转速[5-7]。

3 Simulink仿真

电机基于扩展反电动势的无速度传感器整体控制框图如图1。

根据前理论，可以在Matlab Simulink 环境中建立基于扩展反电动势的面装式永磁同步电动机的无速度传感器控制仿真如图2。

其中，扩展反电动势观察器的构造如图：

需要指出的是，起初提取的速度估算信号噪声较大。因为速度信号是位置信号的微分，在仿真中由于逆变器的非线性，正弦扩展反电动势含有大量噪音，虽然噪音对位置估算影响不大，但一旦微分后势必含有大量谐波信号。因此需低通滤波器在整个系统中是需要的。仿真系统的主要参数，如表1。

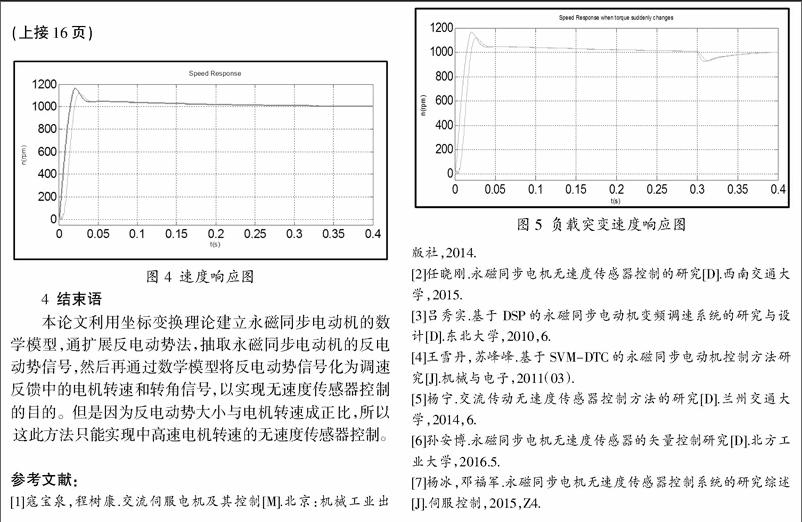
仿真结果，如图4、图5所示，其中左边线为编码器的速度信号，右边线为EMF观察器的速度信号。

为测试系统的抗干扰能力，可将 0.3 秒时突变负载，其仿真结果，如图5所示。

4 結束语

本论文利用坐标变换理论建立永磁同步电动机的数学模型，通扩展反电动势法，抽取永磁同步电动机的反电动势信号，然后再通过数学模型将反电动势信号化为调速反馈中的电机转速和转角信号，以实现无速度传感器控制的目的。但是因为反电动势大小与电机转速成正比，所以这此方法只能实现中高速电机转速的无速度传感器控制。

参考文献：

[1]寇宝泉，程树康.交流伺服电机及其控制[M].北京：机械工业出版社，2014.

[2]任晓刚.永磁同步电机无速度传感器控制的研究[D].西南交通大学，2015.

[3]吕秀实.基于DSP的永磁同步电动机变频调速系统的研究与设计[D].东北大学，2010，6.

[4]王雪丹，苏峰峰.基于SVM-DTC的永磁同步电动机控制方法研究[J].机械与电子，2011（03）.

[5]杨宁.交流传动无速度传感器控制方法的研究[D].兰州交通大学，2014，6.

[6]孙安博.永磁同步电机无速度传感器的矢量控制研究[D].北方工业大学，2016.5.

[7]杨冰，邓福军.永磁同步电机无速度传感器控制系统的研究综述[J].伺服控制，2015，Z4.