基本不等式与“对勾”函数
2018-02-22 03:21:10毛铭
张家口职业技术学院学报 2018年3期
毛 铭
(张家口市第一中学,河北 张家口075000)

一、求最值
例1.已知a、b∈R+,a+b=4,求ab的最大值。
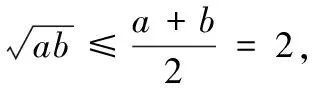
以上形式还可用于应用题。
例2.用一块长为20m的篱笆靠墙围成一块菜园(如图所示),问:长、宽各为多少m时,围成的菜园面积最大?
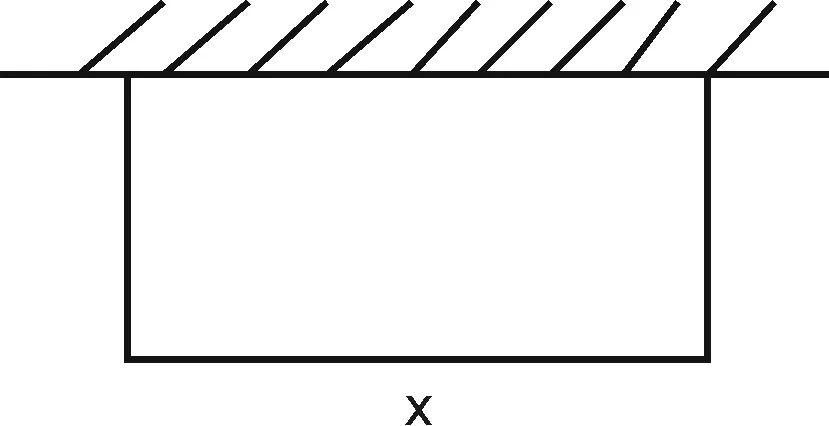
解:该长为xm,0 此时S≤50 ∴当菜园长为10m,宽为5m时,菜园面积最大为50m2。 解:因为第一象限的点(a,b)在直线2x+3y-1=0上,所以2a+3b-1=0,a>0,b>0,即:2a+3b=1 解:由函数f(x)=|lgx|,a>b>0,f(a)=f(b)可知 也可应用于求一些分式型函数的值域。 解:∵x∈R,当x=0时,f(x)=0 还可应用于一些简单不等式的证明。 当且仅当a=b=c时等号成立。 基本不等式应用广泛,但求最值时一定要注意以下两方面: 1.在应用基本不等式求最值时,要把握“一正二定三相等”,“一正”即各项都是正数,“二定”即和或积为定值,“三相等”即等号能取得,这些条件缺一不可。 2.当多次使用基本不等式时,一定要注意多次是否能保证等号成立,并且要注意等号的条件是否一致。在利用基本不等式处理问题时,列出等号成立的条件不仅是解题的必要步骤,而且也是检验转换是否有误的一种方法。 若不注意等号成立条件是否满足,容易犯错误,导致求解结果错误。 得f(x)的值域为[2,+∞) 图像: 我们看上例的解答: 又∵a=1 ∴f(x)在[2,+∞)上单调递增。 总之,弄清基本不等式与“对勾”函数的关系有助于我们更灵活解题,能分清基本不等式的应用条件,有助于理解函数的性质。

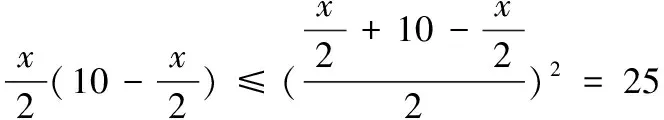
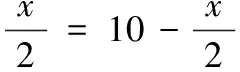
二、配凑法求最值

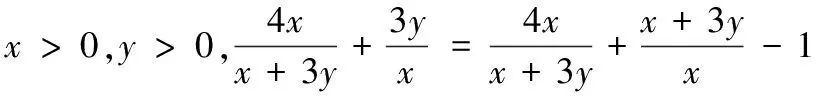

三、通过常值代换法求最值

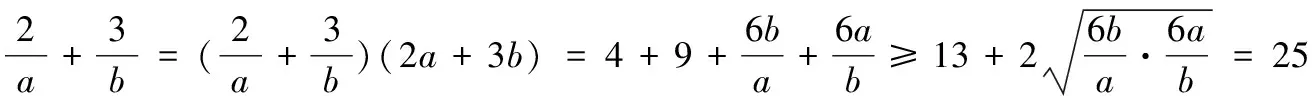
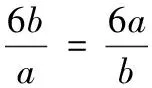
四、通过消元法求最值
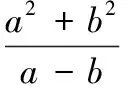
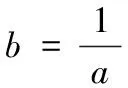
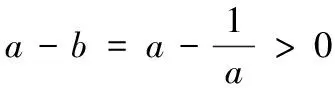

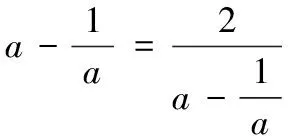
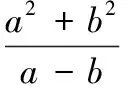




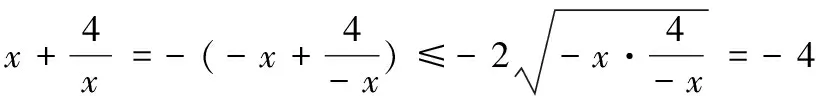
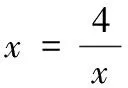
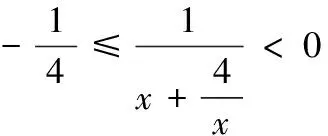


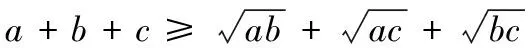
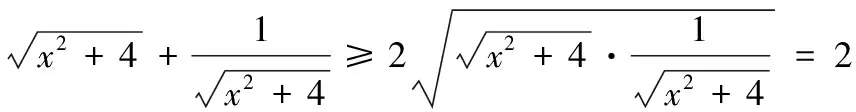
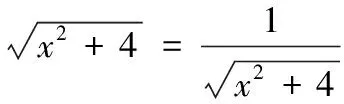


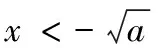
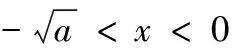



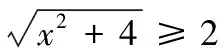

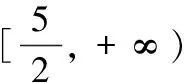

猜你喜欢
中学数学(2022年17期)2023-01-11 01:39:12
中学数学杂志(2022年17期)2022-09-20 07:25:10
中学生数理化(高中版.高二数学)(2022年1期)2022-04-26 13:59:58
新世纪智能(数学备考)(2021年9期)2021-11-24 01:14:32
河北理科教学研究(2020年1期)2020-07-24 08:14:28
新世纪智能(数学备考)(2018年9期)2018-11-08 11:07:34
中学生数理化·高一版(2018年10期)2018-11-08 11:06:56
理科考试研究·高中(2017年10期)2018-03-07 17:40:07
北京航空航天大学学报(2017年5期)2017-11-23 05:53:29
高中生·天天向上(2017年2期)2017-06-09 06:38:14

