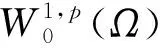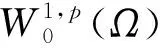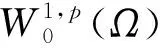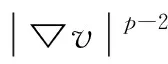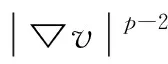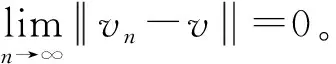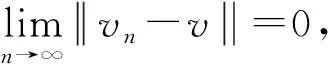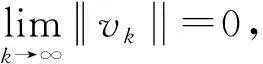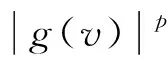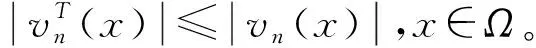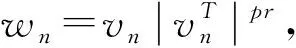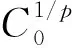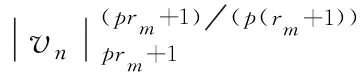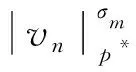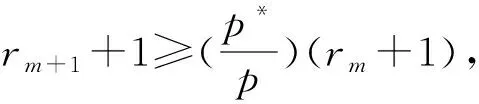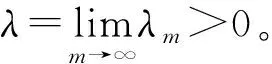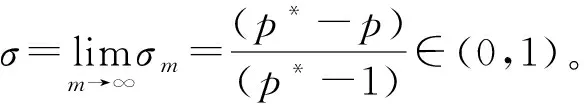一类带有扩散项的p-Laplace方程的无穷多解
景新鹏
(山西大学 数学科学学院, 太原 030006)
本文主要考虑下列问题[1-10]:
(1)
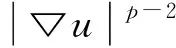
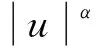
当p=α=2时,方程(1)出现在许多物理模型中,可参考文献[2,5,7]以及相关文献。在这种情况下,Zhou等[10]证明了无穷多小解的存在性。对于带有p-Laplace平方扩散项Δp(u2)u的方程,Uberlandio[8]研究了下面问题:
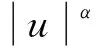
(f1) 存在常数δ1>0,使得当|t|≤δ1时,对所有的x∈Ω,都有f(x,-t)=-f(x,t);
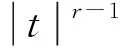
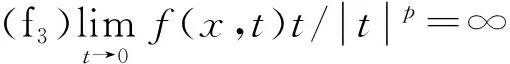
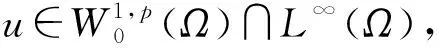
注意到,问题(1)对应的自然泛函为
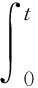
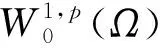
自然地考虑下列问题:
(2)
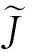
这里|·|∞表示L∞(Ω)上的范数。
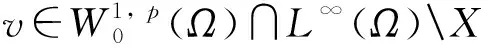
以下给出本文的主要结果:
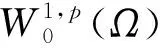
1 准备工作
本节给出一些注记和函数g的一些性质以及需要的定义和引理。
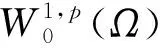
引理1[6]函数g具有下列性质:
①g∈C2(R)是唯一的,并且g在R上是奇函数和可逆函数;
② 0 ③ |g(t)|≤|t|,t∈R; 在证明主要结论之前,需要给出亏格(genus)的定义以及下面的引理。 定义1[1]设E是一个实Banach空间,令Σ(E)={A:A是E中关于原点的对称闭集且A⊂E{0}}。设A∈Σ(E)。若A=∅,则规定A的亏格是0,记为γ(A)=0。若A≠∅,如果存在自然数n,使得存在连续的奇映射ψ∶A→Rn{0},则这样n的最小者(记为n0)叫做A的亏格,记γ(A)=n0;如果不存在这样的n,则规定A的亏格是∞,记为γ(A)=∞。 引理2[4]设E是一个无穷维Banach空间,I∈C1(E,R)是一个偶泛函且I(0)=0。若:(I1) 泛函I下有界且满足PS条件;(I2) 对每一个n∈N={1,2,…},都存在An∈Γn,使得supAnI<0,这里Γn={A∈Σ(E)∶γ(A)≥n},那么下列结论之一成立: ① 泛函I存在1个临界点序列{un},满足un→0,I(un)<0; ② 泛函I存在2个临界点序列{un}和{vn},满足un≠0,un→0,I(un)=0,vn→v,v≠0,I(vn)<0,I(vn)→0。 值得注意的是,在引理2的条件下可以得到:泛函I存在一个非平凡的临界点序列{un},满足un→0,I(un)≤0。 以下利用截断技巧证明定理1成立。 取l∈(0,2-1min{δ1,δ2,C})。定义偶函数η∈C1(R,[0,1]),满足η(t)=1,|t|≤l;η(t)=0,|t|≥2l。 考虑问题 (3) 若v是问题(3)的弱解且满足|v|∞≤l,则由引理1的③知,对任意的x∈Ω,都有|g(v(x))|≤l,从而η(g(v(x)))=1。因此,v是问题(2)的弱解,进而u=g(v)是问题(1)的弱解。 令 |h(x,t)|≤C0, (x,t)∈Ω×R (4) 引理3 泛函I是强制的、下有界的,且满足PS条件。 (5) 其中C1=C0μ1是一个常数。因为p≥α≥2,所以泛函I是强制的、下有界的。 (6) 由式(4)和引理1的②有 结合 (7) ||v||≤β|v|p (8) 由(f3)知,存在常数δ3>0,使得当|t|≤δ3时,对所有的x∈Ω,都有 (9) 取l0∈(0,min{l,δ3}),断言存在常数τ>0,使得对任意的v∈En且||v||≤τ,都有 (10) 其中Ωv={x∈Ω:|g(v(x))|>l0}。 事实上,若式(10)不成立,则存在一个满足||vk||→0,k→∞的序列{vk}⊂En{0},使得 令wk=vk|vk|p,则对所有的k∈N,都有 (11) 显然与式(11)矛盾,因此式(10)成立。 由式(9)知,当t∈[0,l0],x∈Ω时,有f(x,t)≥2pβpC-ptp-1,进而H(x,t)=F(x,t)≥2βpC-ptp。结合引理1的④以及l0 (12) 由条件(f1)可知,当|t|≤l0,x∈Ω时,H(x,t)关于第2变量t是偶的,因此通过式(8)、(10)、(12),对任意的v∈En且||v||≤τ,都有 取ρ∈(0,τ],An={v∈En∶||v||=ρ},有γ(An)=n以及supAnI≤(1-p)p-1ρp<0。 从式(4)和引理1的②可以得到: 结合以上2个不等式,令T→∞,有 (13) 则由式(13)得到 通过迭代,有 其中 因为 所以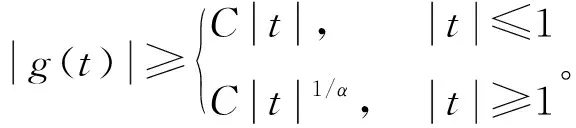
2 主要结论的证明