基于PSO-LSSVM的建筑施工事故预测方法研究

钟燕华

(上海震旦职业学院, 上海 201908)

目前，我国正在进行世界上规模最大的基础设施建设，建筑业已成为国民经济发展的支柱产业之一，对经济可持续发展发挥着重大作用。国家每年对基本建设的投入约占国民生产总值的15%左右，建筑业从业人数约占全国总从业人数的1/3[1]。由于作业条件复杂、高空作业多等特点，建筑业是仅次于矿业的高危行业。因此，做好建筑业的安全管理工作越来越紧迫。建筑施工事故预测可为企业制定安全生产目标和安监部门宏观决策提供依据，是加强安全管理工作的有效途径[2]。

传统的施工事故预测方法有灰色预测方法、神经网络及其改进算法等[3-5]。灰色预测法对呈指数变化趋势的原始样本拟合较好，但是对于数值波动比较大的样本无能为力。神经网络由于存在网络结构难以确定、过拟合等问题，给实际应用带来一定困难。最小二乘支持向量机(least squares support vector machine，LSSVM)能够避免神经网络过拟合和标准支持向量机训练耗时长的问题，泛化能力强[6-9]。LSSVM建模中，模型参数对预测精度有很大影响。粒子群算法(particle swarm optimization，PSO)是一种智能随机优化算法，具有很强的全局搜索能力，非常适合于LSSVM参数优化。

本文采用PSO算法优化LSSVM向量参数，在此基础上构建建筑施工事故预测的PSO-LSSVM模型，并通过仿真实验对模型进行验证。

1 PSO-LSSVM方法的原理

1.1 最小二乘支持向量机

对一组训练样本集D={(xk,yk)|k=1,2,…,N}，其中xk∈Rn，yk∈R，xk表示输入向量，yk表示输出数据，n为训练样本数。在特征空间中LSSVM模型可表示为[10-11]：

y=wTφ(x)+b

(1)

式中：φ(·)表示非线性映射函数；w表示特征空间的权向量；b表示偏置量。

根据结构风险最小化原则，最小二乘支持向量机的函数估计问题可描述为：

(2)

约束条件为：

yk=wTφ(xk)+b+ek

(3)

构建非线性映射函数的目的是提取原始空间的特征，将原始空间中的样本映射到高维空间，从而解决原始空间中的线性不可分问题。根据式(2)，可定义拉格朗日函数如下：

L(w,b,e;α)=J(w,e)-

(4)

式中αk表示拉格朗日乘子，αk∈R。

根据KKT条件，对式(4)进行优化，即：

(5)

(6)

其中：

y=[y1,y2,…,yN],α=[α1,α2,…,αN]

lv=[1,1,…,1],Ω=φT(xk)φ(xl)

(l=1,2,…,N)

根据Mercer条件，存在映射φ和核函数K(·，·),使：

K(xk,xl)=φT(xk)φ(xl)

(7)

由式(6)和式(7)联立求出α和b后，得到LSSVM回归算法的函数估计式：

(8)

式(8)取不同的核函数生成不同的支持向量，主要有B样条核函数、多项式核函数和径向基核函数(RBF)等。为了获得最优的核函数参数σ和误差惩罚参数γ，减少主观经验选取参数的盲目性和重复性，本文采用PSO算法确定最优的σ和γ。

1.2 PSO算法

PSO算法是由鸟类群体行为启发而提出的一种全局优化算法。PSO通过个体之间的协作寻求最优解，尤其善于解决连续域优化问题[12-17]。

PSO初始化为一群随机粒子，通过多次迭代搜索最优解，粒子优劣由适应度函数决定。每个粒子代表一个可能的解向量，通过跟踪2个最优解(个体最优解、全局最优解)来更新自己的位置和速度，实现全局寻优。设粒子的位置和运动速度为别为X和V，d为决策变量的维数，则第i个粒子的参数可表示为：

Xi=(xi1,xi2,…,xid)

Vi=(vi1,vi2,…,vid)

更新策略为：

(9)

(10)

(11)

1.3 PSO优化LSSVM参数

用PSO算法优化LSSVM参数，流程如图1所示，基本步骤如下：

步骤1 初始化PSO算法的参数：群体规模、学习因子、最大迭代次数、粒子的初始位置和速度等。

步骤2 用每个粒子对LSSVM训练样本进行学习，得到各粒子当前位置的训练误差，作为各粒子的适应度值。将各粒子的当前适应度值与该粒子的最优适应度值进行对比，如果更优，则将当前位置作为该粒子的最优位置。

步骤3 用式(11)计算惯性权重，用式(9)、式(10)更新粒子的速度和位置。

步骤4 判断是否满足寻优终止条件(设定的最大迭代次数或精度)，如果满足则求出最优解，如果不满足则转至步骤2。

图1 PSO优化LSSVM参数的基本流程

2 PSO-LSSVM建筑施工事故预测建模

2.1 数据预处理

LSSVM对0到1之间的数据学习效果最佳，为此，在进行机器学习之前首先将原始样本用下式进行归一化处理：

(12)

式中：xi表示原始样本；ximax、ximin分别为原始样本的最大值和最小值，

最后，对建筑施工事故预测结果进行反归一化处理，即：

(13)

2.2 LSSVM预测器的拓扑结构

对于一组给定的样本序列：

{x1,x2,…,xN}

假定已知x(t)，预测x(t+1)，可建立映射函数：

f∶Rm→R

于是

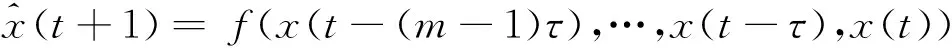
(14)

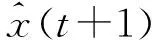
LSSVM预测器的拓扑结构如图2所示。

2.3 适应度函数构建

LSSVM预测器的待优化参数为γ、σ，即：

(15)

参数优化的目的是提高预测精度，构建训练样本的适应度函数：

(16)

图2 LSSVM预测器的拓扑结构

2.4 预测精度评价

通常表征预测结果精度的指标有：平均绝对值相对误差(MAPE)、均方根误差(RMSE)和相对误差(RE)等。本文采用预测结果的MAPE作为预测精度评价指标[18]：

(17)

3 仿真实验

3.1 数据来源

本文预测样本来源于文献[4]建筑施工事故数据。选择嵌入维数为5，将原始样本分为11组。前9组为训练样本，用于构建LSSVM预测器，后2组为预测样本，用于检验PSO-LSSVM预测能力。

3.2 参数优化

选取核函数为RBF核函数，用LSSVM将重构的建筑施工事故训练样本进行训练。

PSO参数设置为：种群数N=30，最大迭代次数为Gmax=100，学习因子c1=1.5，c2=1.5，惯性权重ω=0.7。在Matlab R2011a环境下优化PSO-LSSVM模型，得到最优的宽度参数σ2=0.34，误差惩罚参数γ=151。

PSO对LSSVM参数的寻优过程如图3所示。从图3中可以看出:PSO对LSSVM的寻优速度很快，经过不到20次迭代基本能够得到最优的LSSVM参数。

图3 PSO参数寻优过程

3.3 模型训练结果及分析

得到最优的模型参数后，对建筑施工事故训练样本进行训练，结果如图4所示。从图4中可以看出:PSO-LSSVM输出值和真实值基本重合，说明建模精度非常高。

图4 建筑施工事故的PSO-LSSVM训练结果

3.4 模型预测结果及分析

用训练好的PSO-LSSVM模型对建筑施工事故进行预测，同时与文献[4]进行对比，结果见表1。

表1 建筑施工事故的PSO-LSSVM预测结果

从表1可以看出：PSO-LSSVM对2008年、2009年的预测结果相对误差均小于5%，能够满足工程精度要求，计算得MAPE(PSO-LSSVM)=2.99%，相比同类文献算法MAPE(灰色马尔可夫)=4.62%而言，PSO-LSSVM对建筑施工事故预测的精度更高，更具先进性。

4 结论

1) 建筑施工事故具有影响因素错综复杂、少样本、随机波动大的特点，用传统预测方法很难进行准确建模，并且计算较为复杂。

2) LSSVM对随机波动较大的样本具有较大优势、泛化能力强。粒子群算法能够运用于LSSVM参数寻优中，并且计算简单、运算速度快，仿真案例验证了2种算法的综合优势。

3) 预测结果表明，采用PSO-LSSVM的平均绝对值相对误差为2.99%，并且每年的预测相对误差都低于5%，能够满足工程应用要求，充分说明了本文所提方法的有效性。

4) 本文借用同类文献的数据，时效性稍差，但不影响说明所建预测模型的正确性和所用方法的先进性。