基于路面附着系数估计的多路况安全距离模型

常 群,孙申鑫,赵宇超,宫 燃

(江苏大学 a.汽车与交通工程学院； b.能源与动力工程学院， 江苏 镇江 212013)

汽车在行驶过程中的安全很大程度上受路面与轮胎之间作用力的影响。在不同附着系数道路状态下，轮胎附着力等力学特性对驾驶安全的影响至关重要。控制环节本质上就是通过对道路附着力的最大利用来保证车辆行驶状态的安全[1]。在低附着系数道路情况下，交通事故风险较大。因此，对于不同路面道路附着系数的估计与判定，是车辆能够安全行驶的基础与保证。

卡尔曼滤波(Kalman filtering)是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。它适用于线性、离散和有限维系统。每一个有外部变量的自回归移动平均系统(ARMAX)或可用有理传递函数表示的系统都可以转换成用状态空间表示的系统，从而能用卡尔曼滤波进行计算。对于非线性的问题，则多运用到无迹卡尔曼滤波( UKF)与扩展卡尔曼滤波(EKF)。两者的重要差异是EKF是对高度复杂非线性系统模型函数进行泰勒展开，对展开式进行一阶线性截断处理，这样便可将模型转化为计算机处理的线性问题，然后进行卡尔曼滤波，因此EKF是一种次优滤波，经常被运用在车辆状态估计领域[2-6]。但由于EKF考虑了泰勒级数的展开，因此大大增加了其运算量。与对非线性函数的近似相比，高斯分布的近似要简单得多。UKF能获得精确到三阶矩阵均值和协方差，具有更高的滤波精度，并且该方法直接使用系统的非线性模型，不需对非线性系统线性化，也不需要像二次滤波那样计算HESSION 和JACOBIAN矩阵，提高了运算速度。应用UKF进行车辆状态与路面附着系数估计，计算量小，准确率高[7-8]。

安全车距是指后方车辆为了避免与前方车辆发生意外碰撞而在行驶中与前车所保持的必要间隔距离。保持安全车距是防止追尾事故最直接、最有效、最广泛和最根本的方法。安全距离模型是车辆安全状态判定的基础,国内外进行了很多相关的研究并提出了多种模型,如基于车间时距的安全距离模型[9-10]、基于车辆制动过程运动学分析的安全距离模型[11-12]、驾驶员预瞄安全距离模型[13-14]等。这些相关的安全距离模型中很多忽略了路面附着系数对安全距离产生的影响。因此本文将路面附着系数的判定作为影响安全距离的重要因素，从而建立更贴合多路况驾驶情况下的车辆安全距离模型。

本文采用 UKF 估计方法对路面附着系数等状态参数进行估计，将估计结果与仿真的实际输出值进行对比分析，以验证估计结果的精确度。之后选取合适的车辆安全距离模型，在此基础上加入对路面附着系数、坡道角等因素的考虑，提出改进后的安全距离模型，使之更加符合实际情况。通过Carsim与Matlab/Simulink联合仿真，得到车辆跟驰状态下前后车的距离与相对速度曲线，验证了模型的可靠性。

1 车辆动力学模型

1.1 整车模型

本文提出的整车模型具有七自由度，包含纵向、侧向、横摆3个方向的运动以及4个车轮的回转运动。

以车体质心为坐标系原点，X轴为车辆纵向的对称轴，向前为正；Y轴过质心，向左为正。水平的内力矩和回转角以逆时针方向为正。以此条件建立车体坐标系，得到如下运动微分方程:

纵向方程

(1)

Fx4-(Fy1+Fy2)sinα]

(2)

式中:vx为车辆纵向速度；αx为车辆纵向加速度；vy为车辆侧向速度；α为前轮转角；m为整车质量。Fy1与Fy2分别为左前轮和右前轮上侧向力；Fx1、Fx2、Fx3与Fx4分别为4个车轮上的纵向力。

侧向方程

(3)

Fy4-(Fy1+Fy2)cosα]

(4)

式中:ay为车辆侧向加速度；Fy3与Fy4分别为左后轮与右后轮上的侧向力。

横摆方程

(Fy1+Fy2)cosα-B(Fy3+Fy4)]

(5)

(6)

式中:Iz为绕垂直轴线的转动惯量；γ为横摆角速度；tf与tr分别为前轮和后轮的距宽；A与B分别为质心到前轴与后轴的距离。

1.2 轮胎模型

本文采用修正之后的Dugoff轮胎模型，设Fxi为纵向力，Fyi为侧向力，i=[1,2,3,4],则有如下公式：

(7)

(8)

(9)

(10)

式中:μ为路面附着系数；Fzi为作用在各轮上的垂向载荷；Cx为轮胎的纵向刚度；Cy为轮胎的侧偏刚度；λi为各轮胎纵向滑移率；L为边界值，表述了轮胎非线性特性；βi为各轮胎侧偏角；ε为速度影响因子，作用在于修正轮胎滑移的速度对轮胎力的影响。

经过归一化处理后，Dugoff轮胎模型数学表达式可以表示为：

(11)

由此可得前后轮垂直载荷的数学表达式：

(12)

式中:l=A+B，为前后轴距；df为前轴轮距;dr为后轴轮距；h为整车质心高度。

1.3 四轮车辆动力学模型

本文在Dugoff轮胎模型基础之上建立四轮车辆动力学模型，可实时估计汽车在行驶过程中的路面附着系数，进而得到关于路面附着系数的状态模型。方程如下：

(13)

式中μ1、μ2、μ3、μ4分别为4个轮胎的路面附着系数。

2 基于UKF的路面附着系数估计

2.1 无迹卡尔曼滤波算法

UKF是一种新型的滤波估计算法。该滤波算法以UT变换为基础，摒弃了对非线性函数进行线性化的传统做法，采用卡尔曼线性滤波框架，对于一步预测方程，使用无迹(UT)变换来处理均值和协方差的非线性传递，就成为UKF算法。UKF是对非线性函数的概率密度分布进行近似，用一系列确定样本来逼近状态的后验概率密度，而不是对非线性函数进行近似，不需要求导计算Jacobian矩阵。UKF没有线性化忽略高阶项，因此非线性分布统计量的计算精度较高。UKF相较于EKF，两者对线性系统具有相同的估计性能；对非线性系统，UKF具有更高的滤波精度和稳定性。

对上一节提到的非线性汽车系统，其过程噪声和观测噪声的Q与R对UKF的滤波精度具有重要影响，原因在于Q与R决定当前信息与前一时刻信息之间的权重。而这两种信息直接影响UKF递推的精度。本文在估计路面附着系数过程中，假设过程噪声和观测噪声均为高斯白噪声，则UKF滤波算法过程如下：

1) 初始化均值和协方差

(14)

(15)

车辆在直线行驶状态下横向的动力学参数变化较小，为了保证该算法收敛从而得到较为准确的车轮纵向力及滑移率的估计值，将P0设置为单位矩阵。

2) 计算Sigma点

(16)

(17)

(18)

(19)

该方程式中：ε=τ2(n+k)-n,该参数用来控制Sigma点与均值间距离，用以确定Sigma点的散布程度，通常取较小正值。考虑所用轮胎模型具有较强的非线性特性，本文中ε=0.01。为保证方差矩阵半正定性，本文k=0。在高斯分布情况下，取γ=2为最优值。

3) 时间更新过程

首先计算预测样本点：

Xi,k+1|k)=f(Xi,k|k,uk))+qk

(20)

再计算均值和方差：

(21)

(22)

φi,k+1|k)=h(Xi,k+1|k))

(23)

(24)

4) 量测更新过程

(25)

(26)

(27)

(28)

(29)

2.2 基于UKF的路面附着系数模型建立

为了让变量便于从传感器中得到或是间接估计得到，结合四轮车辆动力学模型，在估算路面附着系数时，选取式(30)作为测量方程，以各轮的路面附着系数作为系统的状态变量，即x=[μ1,μ2,μ3,μ4]，输入的控制变量u=α，输出y=[ax,ay,γ]。

测量方程如下：

(30)

式中：βi、vi、λi、ωi分别表示各轮的侧偏角、速度、滑移率和车轮转速；vcog为汽车质心速度。

轮胎模型的输入为：轮胎侧偏角β，各轮转速ω1、ω2、ω3、ω4，纵向和侧向的加速度ax和ay，纵向车速vx，横摆角速度γ，质心侧偏角δ。

3 车辆安全距离模型的建立

本文在运用UKF方法初步判断路面附着系数的基础上，需建立真实有效的安全距离模型。A与B两车在同一车道上行驶，设自车为A，前车为B，前车与后车在A制动的刹那相距为D。A车采取制动一段时间之后，A的行驶距离为Sa，B的行驶距离为Sb，这时两车间的距离为d0。该制动过程如图(1)所示。

图1 车辆制动过程距离

安全距离的公式为：

D=Sa-Sb+d0

(31)

自车和前车的主要运动状态可分为4种：静止、匀速运动、加速运动和减速运动。可分为4种情况建立安全距离模型：

1) 前车B静止，自车以速度va接近前车B。此时，Sb=0，A的运动过程分为3个阶段：驾驶员反应阶段、制动器作用阶段和持续制动阶段，则安全距离公式可表示为：

(32)

其中：t1包含了驾驶员反应时间；t2为制动器的作用时间。

2) 前车B以速度vb匀速行驶，自车A以va的初速度(va>vb)，aa的减速度接近前车B，当va=vb的瞬时，两车保持的车距大于或等于最小安全车距。则有如下表达式：

(33)

(34)

安全距离公式可表示为：

(35)

3) 前车B以减速度ab制动直至停止。当出现B静止时A仍然处于行驶状态时为危险情况，可能会发生追尾。此时A与B的制动距离可由以下表达式表示：

(36)

(37)

安全距离公式可表示为

(38)

4) 前车B向前加速行驶，此时可能出现两车有发生追尾的可能和没有发生追尾的可能两种情况。经综合分析，第2种安全距离模型可以完全满足使用条件。

为了更加贴合实际情况，本文在该安全距离模型的基础之上引入路面附着系数与坡道角。不同的路面对车辆制动效能以及制动的距离具有较大的影响。坡道的主要影响在于车辆制动时，自身的载荷会发生变化，从而影响制动减速度。综合考虑二者影响，结合本文提到的安全距离公式，可优化为如下安全距离模型：

当前车B处于静止、匀速和加速运动状态时，设D1为安全距离，则安全距离公式为

(39)

当前车B突然减速时，设D2为安全距离，则安全距离公式为

(40)

4 仿真实验分析与结果

4.1 基于UKF的路面附着系数估计仿真

本文选取4种典型路面作为仿真估算的基础，4种路面分别为 干沥青、湿沥青、雪面和冰面。这4种路面的峰值附着系数以及变化范围如表1所示。

表1 4种典型路面峰值附着系数

在4种仿真工况下，在仿真软件中分别将4种路面的附着系数设置值设定为其峰值附着系数的均值。

考虑Dugoff轮胎模型和汽车状态的估计，运用Carsim和Simulink进行联合仿真。分别对4种工况进行仿真分析，将路面附着系数分别设定为0.92、0.70、0.24、0.10，Carsim中模拟方向盘的叫阶跃输入。结果如图2～5所示。

图2 干沥青路面附着系数估计结果

由图2～5可知：应用UKF进行路面附着系数估计，经计算，在干沥青行驶工况下，四轮路面附着系数估计总误差均值为0.007 55，误差在0.821%左右；在湿沥青行驶工况下，四轮路面附着系数估计总误差均值为0.006 02，误差在0.86%左右；在雪地行驶工况下，四轮路面附着系数估计总误差均值为0.003 52，误差在1.46%左右；在冰面行驶工况下，四轮路面附着系数估计总误差均值为0.002 50，误差在2.5%左右。随着路面附着系数的减小，虽然UKF对路面附着系数估计的精度有所降低，但是仍然比较精确，可见UKF对路面附着系数估计精度较高。

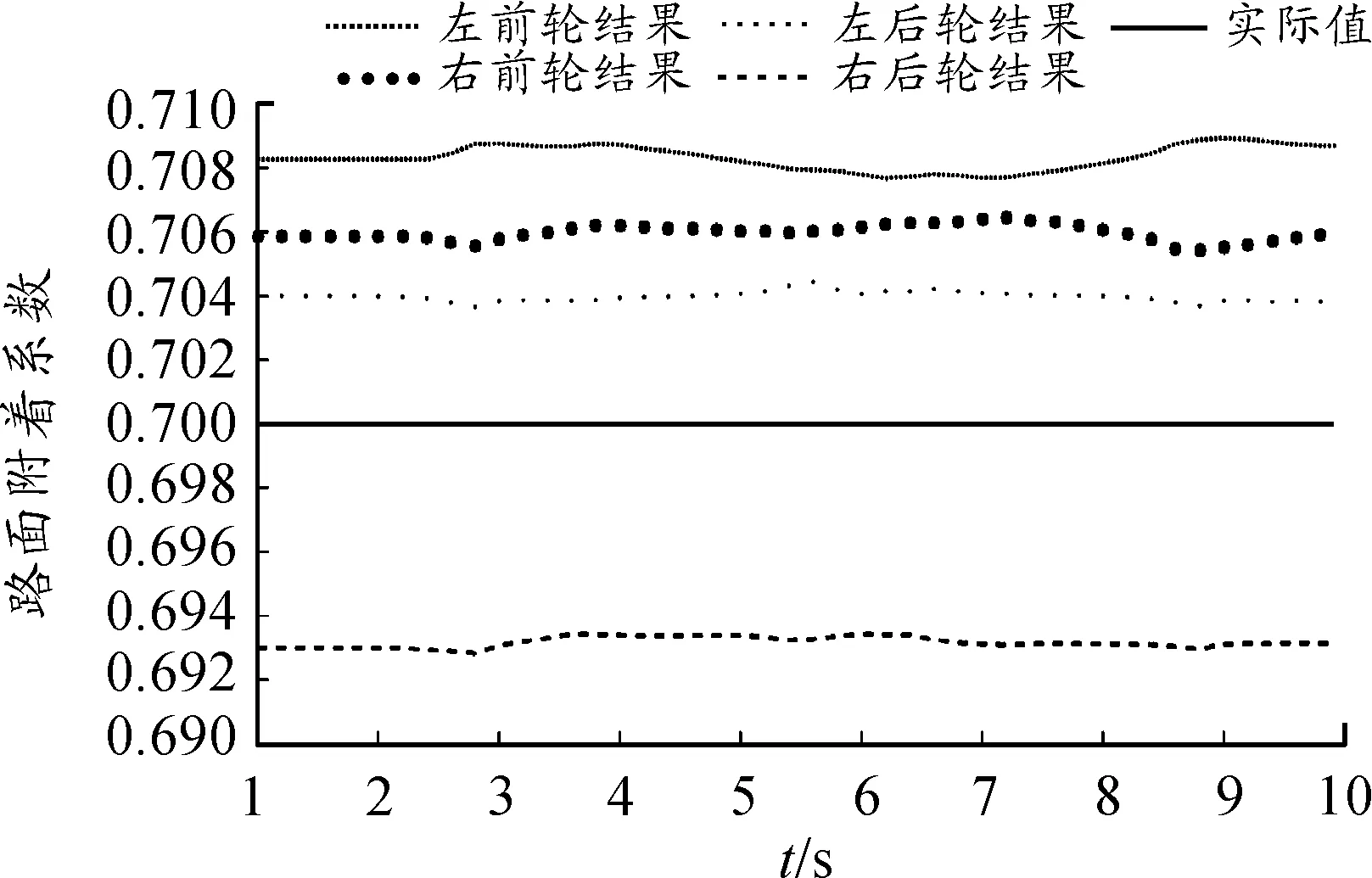
图3 湿沥青路面附着系数估计结果

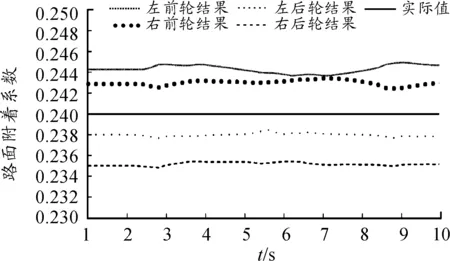
图4 雪地附着系数估计结果

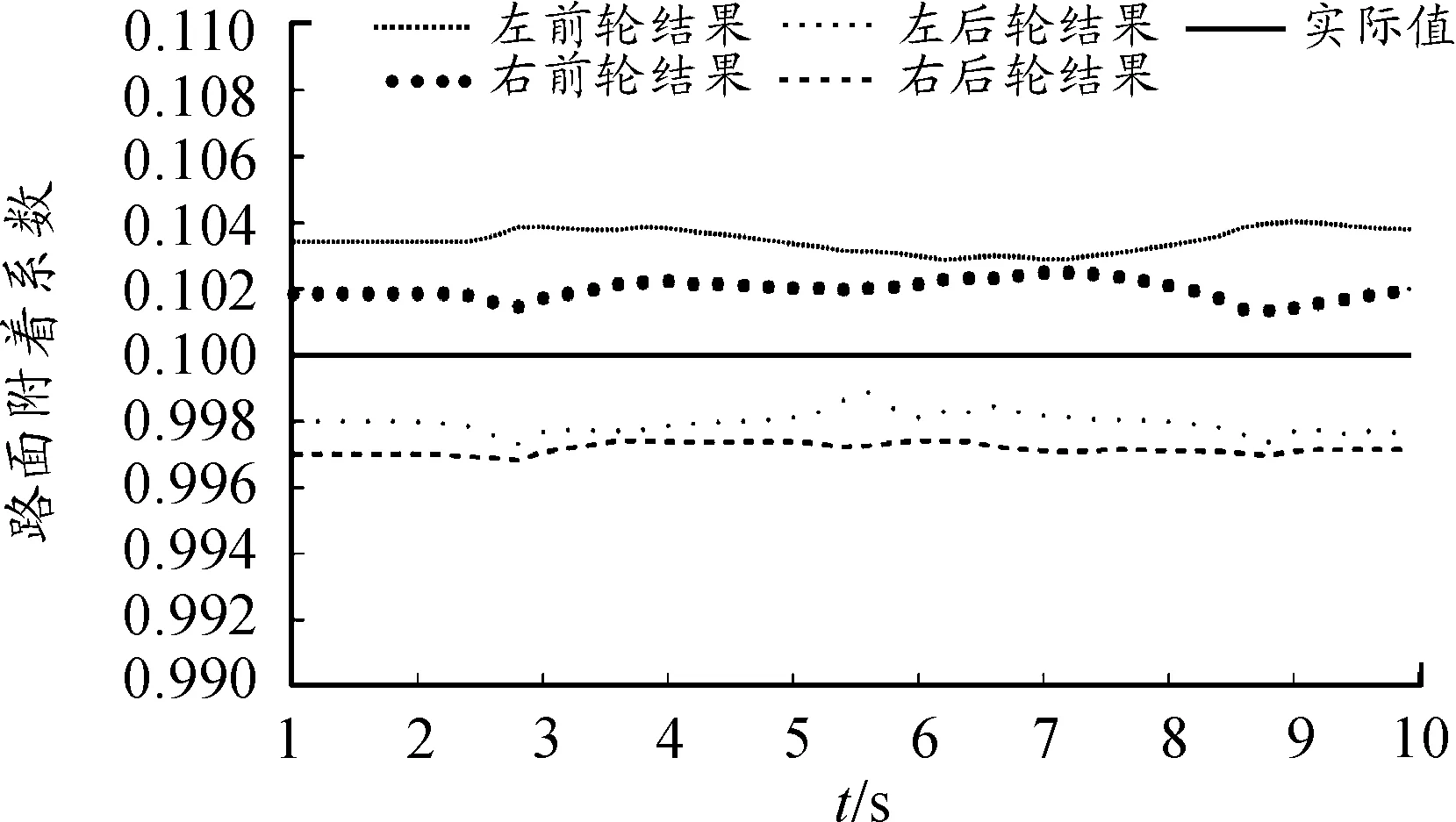
图5 冰面附着系数估计结果

4.2 安全距离模型仿真分析

根据建立的考虑路面附着系数与坡道状态的安全距离模型，搭建车辆跟驰模型。

该跟驰模型中，假设路面环境为宽阔无阻碍路面，设定了前车的运动状态。仿真时间设定为50 s，前车每10 s切换一种运动状态。其中0～10 s、20～30 s、40～50 s三个时间段前车匀速直线行驶，10s-20s时间段匀加速行驶，30～40 s时间段匀减速行驶。具体运动状态如表2所示。

表2 前车分时段运动状态

模型中路面附着系数识别模块由本文上一节建立，由于输出是整车的路面附着系数，假设路面平直无颠簸，故将四轮的路面附着系数取均值作为整车路面附着系数的估计值。设定坡道角θ=10°，后车初速度va=25 m/s，在相对距离运算模块中，输入的控制变量u=[va,vb,ab,μ,θ]，输出量为相对距离y=[D]，分别模拟两车在4种路面情况下的跟驰状况。

1) 干沥青路面仿真情况见图6。

2) 湿沥青路面仿真情况见图7。

3) 雪地路面仿真情况见图8。

4) 冰面仿真情况见图9。

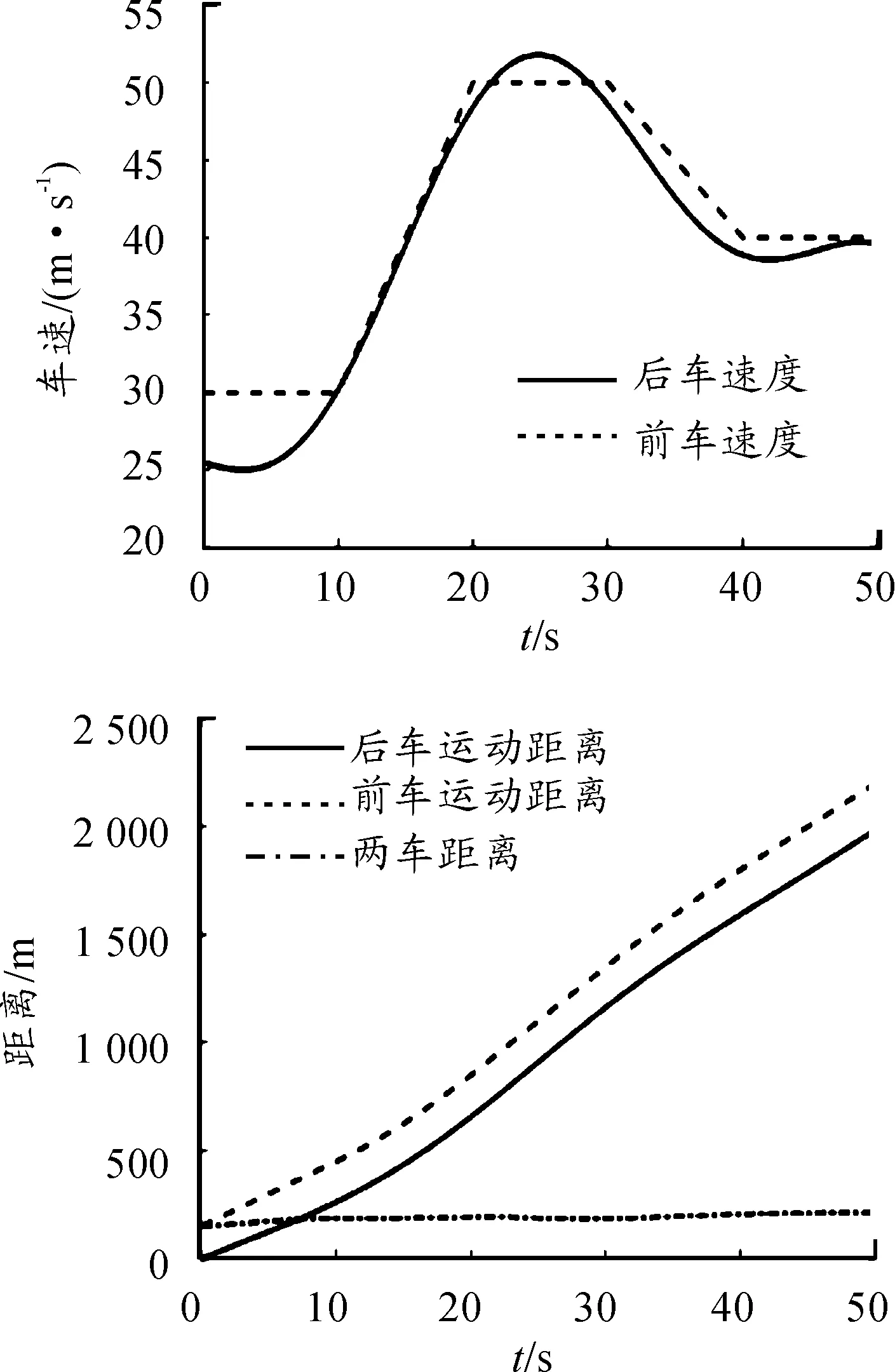
图6 干沥青路面两车相对车速/相对距离变化曲线

图7 湿沥青路面两车相对车速/相对距离变化曲线

图8 雪地路面两车相对车速/相对距离变化曲线

由图6～9可知：在干沥青、湿沥青、雪地和冰面4种路况下，后车在经过短暂的迟滞后开始加速，与前车的速度变化曲线有较好的重合度，说明在运动过程中跟车效果良好。相对距离变化较小，保证了跟车的平稳性。随着路面附着系数的减小，两车的相对距离相应增大。符合之前安全距离公式中呈现的规律。

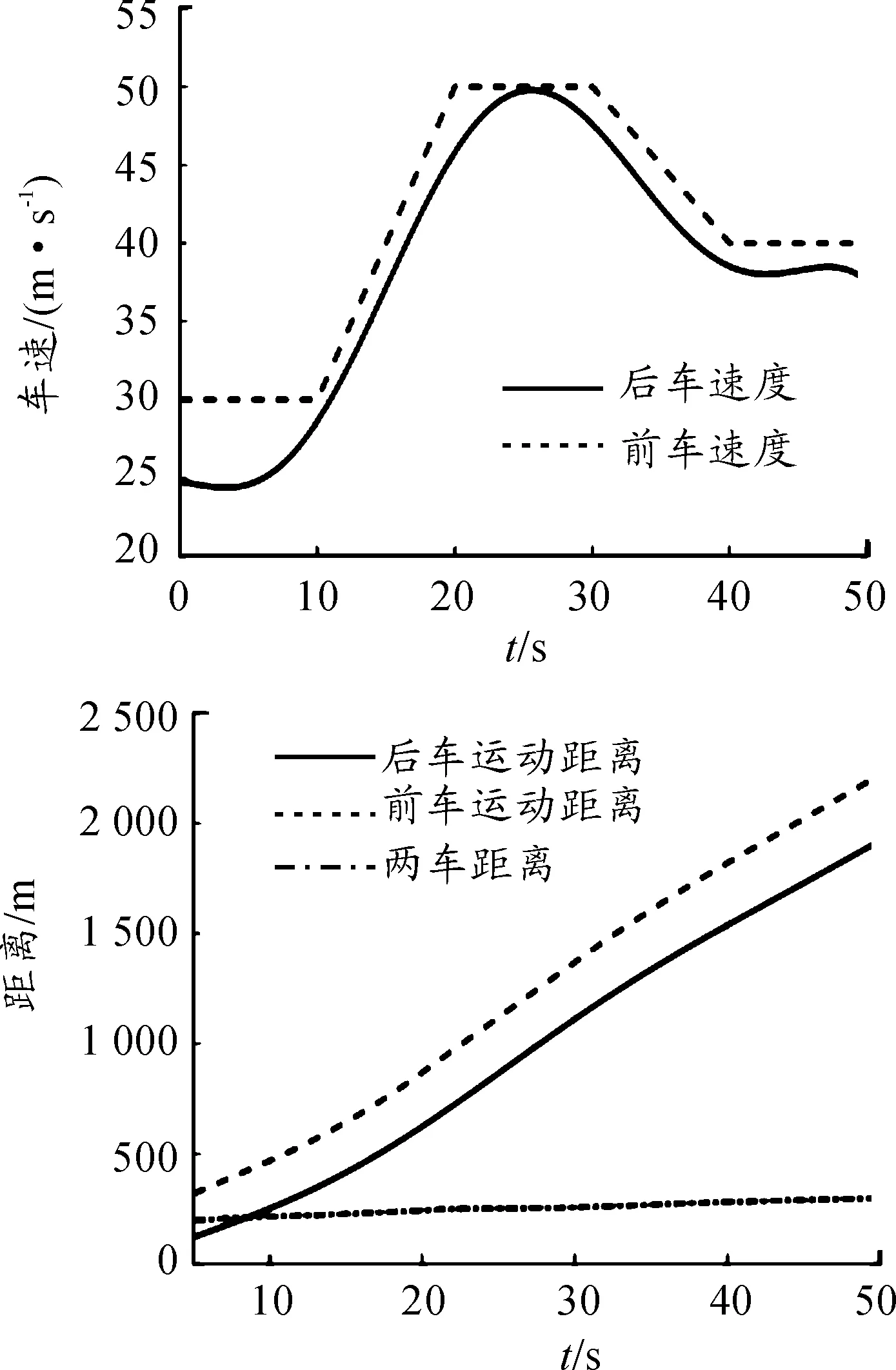
图9 冰面两车相对车速/相对距离变化曲线

5 结论

1) 利用UKF结合四轮车辆动力学模型对四种典型路面(干沥青、湿沥青、雪地、冰面)附着系数进行估计，运用Carsim与Simulink联合仿真，得到的结果是每个轮胎的附着系数估计值与设定值的误差都控制在3%以内，表明该方法仿真结果较为准确。

2) 对已有的安全距离模型进行改进，加入路面附着系数与坡度的考量，使之更加贴合实际情况。利用UKF输出的各车轮的路面附着系数作为该安全距离模型的一个输入，仿真后得到后车的速度能够较好地跟随前车速度的变化而变化，两车的距离也能够保持在安全距离范围内，并且波动情况平稳，表明该模型能够较好地反映跟车的情况。