浅谈因式分解的教学方法与技巧

广东省东莞市东城区品尚实验学校 冯韵珊

在中学数学教学中，多项式因式分解是一种重要的代数变形方法，被广泛地应用在初等数学之中，是我们解决许多数学问题的有力工具，不仅用于计算代数式的化简，求值解方程和不等式代数内容，而且在几何、三角等解不等式代数中扮演重要角色.因此学习这些方法与技巧，不仅是掌握因式分解内容所必需的，而且对于培养学生的解题技能，发展学生的思想能力，都有着十分独特的作用.本文通过实例教学说明因式分解的方法与技巧。

一、提取公因式法

各项都含有的公共的因式叫做这个多项式各项公因式.若多项式各项含有公因式，可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式，这种分解因式的方法叫做提取公因式法.

方法：当各项系数都是整数时，公因式的系数应取各项系数的最大公约数字母取各项的相同的字母而且各项字母的指数取次数最低.如果多项式的第一项是负的，在教学中要强调提出“-”号，使括号内的第一项的系数成为正数.提取“-”号时，注意多项式的各项都要变号.

例1：分解因式.

分析：这是一个简单的二项式，各项系数(2 4 .18.28)的最大公因数为2,因为第一项是负的，所以最大公因数为-2，各项字母x最低指数为1，可以直接提取公因式-2x.

点悟：通过分析、观察，提出公因式.

口诀：找准公因式，一次要提尽，全家都搬走，留“1”把家守，提负要变号，变形看奇偶.

二、公式法

如果把乘法公式反过来，就可以把某些多项式分解因式，这种方法叫公式法.

1.最基本的公式

平方差公式：a2-b2= (a+b) (a-b) .

完全平方公式：a2± 2ab+b2=(a±b)2.

2.其他重要公式( )

立方和公式：a3+b3= (a+b)a2-ab+b2.

立方差公式：a3-b3= (a-b) (a2+ab+b2) .

完全立方公式：a3± 3a2b+ 3ab2±b3=(a±b)3.

公式：a+b+c- 3abc= (a+b+c) (a+b+c-ab-bc-ac).

例2：因式分解x4-81.

分析：对于只有两项的多项式应选的平方差公式a2-b2= (a+b) (a-b)进行分解.将分解成，将81分解成92，可得：

点悟：分解因式时，应分解到底.

例3：因式分解x4- 2x2y2+y4.

分析：对于只有三项的多项式应选择完全平方公式a2± 2ab+b2=(a±b)2或者x2+ (p+q)x+pq进行分解.将x4，y4完全平方：

点悟：套用完全平方公式，再化简分解的结果.能运用完全平方公式分解因式的多项式必须是三项式，其中有两项能写成两个数（或式）的平方和的形式，另一项是这两个数（或式）的积的2倍.

小结：学生运用公式法的关键是熟悉公式，而这些公式都是把乘法公式反过来得到的.只有掌握并牢固记住各公式的形式和特点，善于观察出一个多项式能否化成符合公式的模型结构，才能准确的利用公式分解.

三、十字相乘法

利用十字交叉线来分解系数，把二次三项式分解因式的方法叫做十字相乘法.

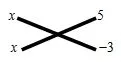
点悟：找系数间的关系.

例5：因式分解 5x2+ 6xy- 8y2.

分析：这个多项式可以看作是关于x的二次三项式，把-8y2看作常数项，在分解二次项及常数项系数时，只需分解5和-8，用十字交叉线分解后，经过观察，选取合适的一组：

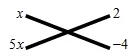
点悟：把系数和主次元结合.(小 结)：十字相乘法有两种情况：（1）x2+p+qx+pq型的式子的因式分解，这类二次三项式的特点是：二次项系数是1；常数项是两个数的积；一次项系数是常数项的两个因式的和.因此，可以直接将某些二次项的系数是1的二次三项式因式分解为(2)型式子的因式分解，如果有且有时，那么

口诀：首尾分解，交叉相乘，求和凑中.

四、双十字相乘法

双十字相乘法属于因式分解的一类，类似于十字相乘法.双十字相乘法就是二元二次六项式，原始的式子如下：ax2+bxy+cy2+dx+ey+f（x，y为未知数），其余都是常数.

步骤：(1)先用十字相乘法分解二次项； (2)先依一个字母的一次系数分数常数项.如十字相乘法；（3）再按另一个字母的一次系数进行检验，如十字相乘法,这一步不能省，否则容易出错；（4）纵向相乘，横向相加.

例6：因式分解x2+ 5xy+ 6y2+ 8x+ 1 8y+ 1 2.

分析：这是一个二次六项式，可考虑使用双十字相乘法进行因式分解.

解：图如下，把所有的数字交叉相连

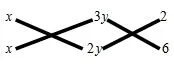
原式 = (x+ 2y+2 ) (x +3y+6).

小结：双十字相乘法是在十字相乘法的基础上产生的，即经过两次十字相乘法再得出结果的，例题中的做法就是按照了以上步骤进行才得以解决，这种做法不难，无非就是分成两步，然后逐步求解因式.

五、分组分解法

利用分组来分解因式的方法叫做分组分解.分组分解法是因式分解中较为复杂的一种方法，是提取公因式和公式法的综合运用，只能用于有四项或六项还有大于六项的方程，一般的分组分解有两种形式：二、二分法，三、一分法.

例7：因式分解x3+x2y-xy2-y3.

分析：将原式的四项分为两组，先提取公因式x2，y2可按二、二分法进行因式分解.

点悟：分组方法、提取公因式法与完全平方公式法结合运用.

(拓展)因式分解x2- 6xy+ 9y2- 5x+ 1 5y.

解：x2- 6xy+ 9y2- 5x+ 1 5y（3-2分组）

= (x- 3y)2- 5 (x- 3y) (前三项用完全平方式分解，后两项提取公因式）

= (x- 3y) (x- 3y- 5 ).（继续提取公因式）

小结：（1）二、二分法的步骤：分组后每组可提取公因式或利用公式进行分解；各组分解后，两大项仍可继续提公因式分解；（2）三、一分法的步骤：三项一组的可用完全平方公式分解；两大项可用平方差公式继续分解.

六、换元法

有时在分解因式时，可以选择多项式中的相同部分换成另一个未知数，然后进行因式分解，最后再转换回来，这种方法叫做换元法.

例8：因式分解(x+y- 2xy) (x+y- 2 ) + (xy- 1 )2.

分析：此式中有相同项x+y，xy，可以令x+y=m xy=n再进行计算.

点悟：解题时应灵活采用多种方法进行因式分解.

注意：换元后勿忘还原.

小结：这两题中的项数和次数比较高，结构复杂，如果全部展开会把问题复杂化，所以可考虑对相同的部分进行换元，把问题变得简单化，这样更容易分解因式.

七、拆、添项法

这种是把多项式的某一项拆开或者填补上互为相反数的两项（或几项），使原式适合于提取公因式法、运用公式法或分组分解法进行分解.要注意，必须在与原多项式相等的原则下进行变形.

例9：因式分解x4- 3x2y2+y4.

分析：上式可先考虑拆项，再分解.因为x4+y4是x2与y22的2平方和，缺少含 2x2y2项.故将 - 3x2y2拆成 - 2x2y2与-xy的和，将原多项式变形为四项式，再进行因式分解.

点悟：拆项前、后的值不变，分组后灵活运用公式进行因式分解.

小结：通过整理几个同类项合并或将两个仅符号相反的同类项互相抵消，但是这里需要恢复那些被合并或相互抵消的项，可用添项和拆项法.

综上所述不难发现，因式分解是把一个多项式分解成几个整式乘积的形式，它和整式乘法互为逆运算，在初中代数中占有重要的地位和作用，在其它学科中也有广泛应用，在初中教育教学中应注意以下几点：

1.因式分解的对象是多项式；

2.因式分解的结果一定是整式乘积的形式；

3.分解因式，必须进行到每一个因式都不能再分解为止；

4. 结果如有相同因式，应写成幂的形式；

5. 因式分解的一般步骤是：

（1）通常采用一“提”、二“公”、三“分”、四“变”的步骤。即首先看有无公因式可提，其次看能否直接利用乘法公式；如前两个步骤都不能实施，可用分组分解法，分组的目的是使得分组后有公因式可提或可利用公式法继续分解；

（2）若上述方法都行不通，可以尝试用双十字相乘法、换元法、拆项、添项法等方法.