某产品总装过程线束敷设问题的灰色关联分析

王家杰

（同济大学，上海 200092）

1 灰色关联分析法

对于两个系统之间的相关因素、相互变化关联大小的量度称之为关联度，它一定意义上反映了一个系统对另一个系统的作用及影响。常用图表趋势表达是为了体现关联度作用及影响程度。趋势吻合则可视为目标范围缩小，为实施精准分析提供方向。

但是，常用图表中的趋势分析有其一定局限性，当分析各个子系统单位不同、子系统较多、数值差异较大或者样本量过多时，需要在两个系统之间进行有量化量度，难度较大。

灰色关联分析法很好解决了上述问题，该方法无需知道两个系统之间的直接原因，仅利用一定计算方式对系统中各因素关联性进行数值计算，将原始观测数据进行无量纲化处理后，计算关联系数、关联度，并根据关联度大小对待评价指标进行排序。

2 灰色关联分析在线束敷设问题中的探索

2.1 某产品总装中线束敷设问题特点

某产品总装线中，通过人工操作进行线束敷设、端接以及设备连接。不同于汽车线束敷设，采用在线束厂完成成品线束，并在汽车上直接敷设、端接。某型号飞机由于结构的高度紧凑，线束较多均，可通过机体结构减轻孔、缝隙来完成线束敷设，达到减轻飞机重量、增大舱内结构空间的目的。而线束敷设中存在的人为因素质量问题，由于问题多、重复性差，在快速分析改进方面存在困难。

2.2 利用灰色关联分析的设想

导致人为发生错误必然有相应诱因，而分后发现诱因可达百余个，这样对单个问题进行详细剖析将花费大量时间，而且分析依赖于一些故障现象和一些复现试验。每个问题和差错成因来说，它们之间关系极为复杂，一个问题的差错可能由多个差错成因引起，这些成因之间有主次之分，难以通过传统问题分析法进行统计分析。反之，一个差错成因也可以引起多个模式差错发生，这些特定模式差错发生的机会也有大小之别，换句话说，某些差错成因导致特定模式差错的可能性非常高。因此，采用灰色关联分析方法对关联程度进行量化分析，利用不同的问题类别与已知可能影响因素对导致线束敷设因素开展分析，对样本量大小没有太高要求，分析时也不需要了解典型分布规律，具有广泛的实用性。

2.3 利用灰色关联进行分析及计算过程

对于每一个问题，组织专家以及操作人员进行仔细细致分析及回忆，每一项差错通过挑选HFACS-S中与线束敷设可能相关的问题原因进行判断，符合则纳入计算，不符合则为0，不纳入数据，统计结果如表1所示。

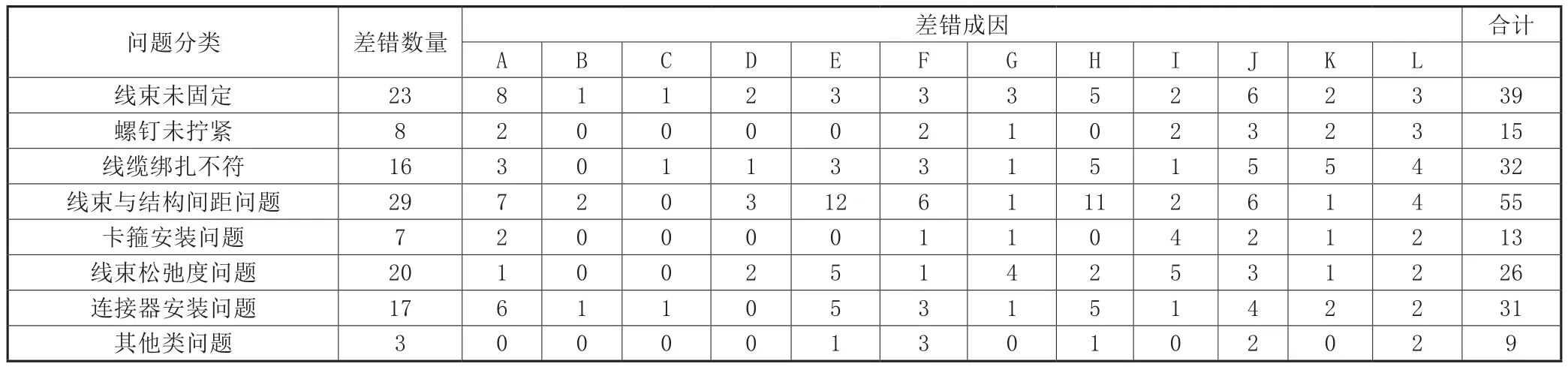
表1 灰色关联问题原因统计表

表中各字母分别代表各问题大类，具体图表2所示。

运用灰色关联分析方法，分析特定差错与各差错成因之间的关联度，灰色关联分析方法的具体计算流程如下：

（1）确定分析序列。设因变量数据构成参考序列X0´，各自变量数据构成X0´(i=1,2,…,n)，n+1个数据序列形成矩阵；

（2）对变量序列进行无量纲化；

（3）求绝对差数列、最大差和最小差。计算第1列（参考序列）与其他各列（比较数列）的绝对差值，得到绝对差值矩阵。绝对差值阵中最大数和最小数即为最大差和最小差：

（4）计算关联系数并进行关联度排序。将各个比较序列与参考序列的关联度从大到小依次排序，关联度越大，说明比较序列与参考序列变化的态势越一致。灰色关联分析方法主要用于经验和数据都较少的不确定性问题，与传统的多因素分析方法相比，灰色关联分析方法具有数据的要求较低，且计算量小的优点。计算结果如表3所示。

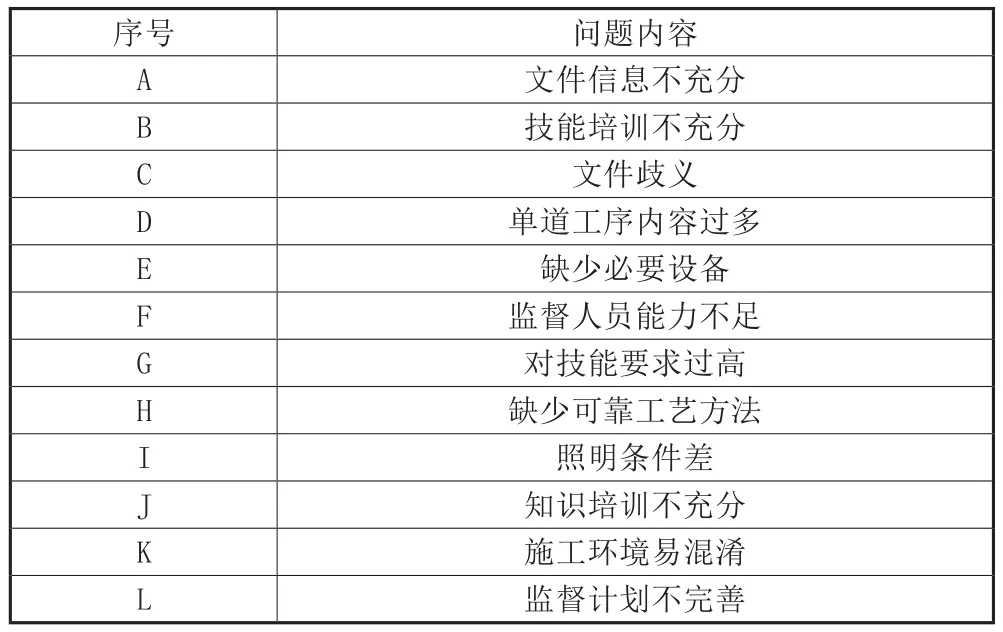
表2 各类问题内容

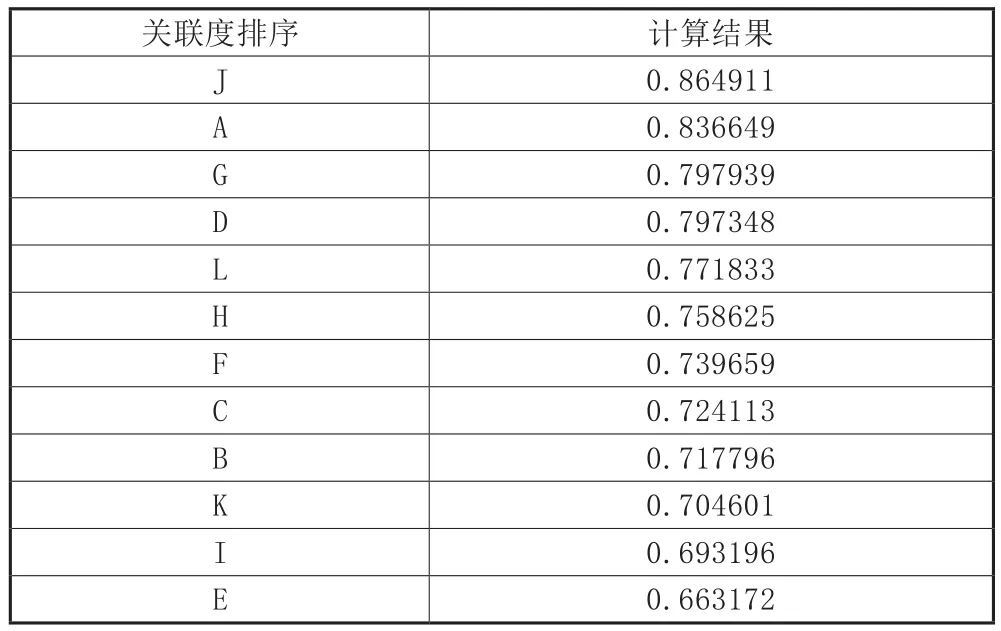
表3 灰色关联分析法计算结果

3 分析结论与改进策略

每行数据按照关联度得出的数值大小直接排序，即可得到线束敷设问题和差错成因之间的对应关系，从而揭示整体线束敷设问题与各差错成因两者之间的规律，并给出定量决策依据，为操作差错预测和预防提供有效指导。将与差错关联度最高的三类原因，即知识培训不充分、文件信息不充分和对技能要求过高作为线束敷设问题分析及改进重点。此时可进一步利用HFACS人为因素分析模型对不安全行为、不安全行为的前提、不安全行为的监管和组织管理四个方面进行深度剖析和完善，并充分利用PFMEA等手段对可能存在的失效模式进行改进。