基于筋板布局的立柱结构优化设计

邓 涛 昃向博 吕守堂 公培强 张 乾

（1.济南大学 机械工程学院，济南 250022；2.济南第一机床有限公司，济南 250000）

数控立式车床是一种自动化程度高、结构复杂、加工精度高的加工设备，主要用于加工精度较高或结构较为复杂的大型或重型盘类零件。数控立式车床主要由底座、立柱与横梁组成。立柱作为数控立式车床的关键部件，支撑连接机床各零部件，同时承受来自切削力等各种载荷作用，其结构是否合理对机床加工精度、工作稳定性、加工效率以及使用寿命都有很大的影响[1-3]。

相关研究人员提出数控机床大件结构设计元结构和基本框架概念，运用有限元分析法对简化床身结构进行动静态特性研究，并将该方法广泛应用于数控机床优化设计中[4]。另外，部分学者提出了基于拓扑优化与筋板布局的立柱轻量化设计，实现了立柱结构的轻量化设计[5]。我国目前多数学者，使用有限元分析软件获得磨床床身固有频率和振型，讨论不同筋板结构布局以及不同部位筋板厚度，对床身动态特性进行研究[6]。

本文以济南第一机床有限公司的J1VL-600数控立式车床为研究对象。该机床采用模块化设计，既能够满足刹车盘单刀架标准车削要求，也满足其他零件标准车削要求。在实际加工过程中发现该机床在高速或重载情况下精度保持性不够，比如在轮毂车加工时会出现网纹现象，严重影响了机床加工精度。分析机床结构发现立柱在切削力及机床其他零部件自重力等外力作用下，会产生很大弯曲和扭转变形，因此需要针对立柱结构进行优化。

针对立柱结构优化有两种思路：第一，运用拓扑优化得到立柱结构基本外形，观察立柱的结构特点可得立柱中空，四面立壁均为一面开口，三面封闭，内部结构复杂，难以运用拓扑优化；第二，对立柱各结构尺寸进行优化，达到轻量化设计要求。本文从立柱内部结构出发，基于元结构优化设计方法，研究筋板选型、布局以及与立柱静动态特性之间的关系，并找出其中规律，从而提高立柱静动态特性。

1 立柱的有限元分析

1.1 立柱结构介绍

J1VL-600数控立式车床立柱是中空、三面立壁上有开孔的薄壁结构，如图1所示。具体尺寸为565mm×600mm×1390mm，四面壁厚均为25mm，加强筋厚度为20mm，其材料为HT300。

立柱通过螺栓连接到底座，在前壁面通过“直线导轨—横梁—滑枕”与刀架系统连接，实现刀具X、Z向进给。与周围相连零部件的装配关系如图2所示。

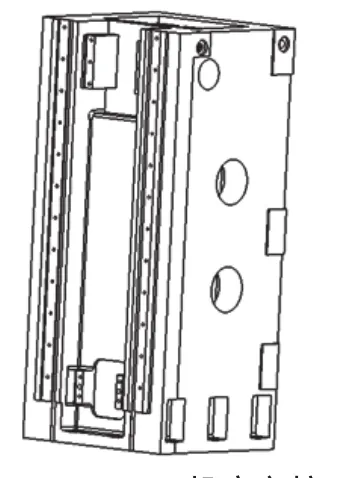
图1 J1VL-600机床立柱

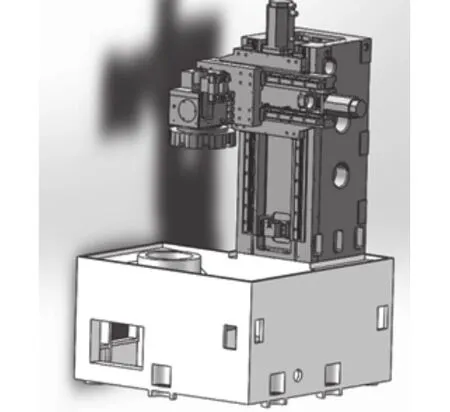
图2 机床整机装配图

该机床立柱内部原筋板布置为左右侧壁面采用太阳筋板，如图3所示；后壁面为井字型筋板，如图4所示。这些加强筋形状和分布虽然规整，但没有考虑在机床加工工件时的应变和应力分布，造成部分加强筋没有发挥其应有的分担变形和承受外载荷功能。本文就该机床立柱应选取何种型式加强筋以及如何布置进行分析计算。

图3 侧面筋板布置

图4 后面筋板布置

1.2 切削力计算

车削加工过程中，切削加工产生的力会对刀具和工件产生一对反作用力，力的大小相等，工件作用在刀具上的合力如图5所示，可以分解为三项：第一，主切削力Fc，作用于主运动方向，是计算机构主运动强度及选择切削用量等的主要依据；第二，背向力Fp，作用在工艺系统刚性最差的方向上，会造成振动、加工误差，是校验机床刚度的必要依据；第三，进给力Ff，是校验进给机构强度的重要依据，且在进给机构上作用。

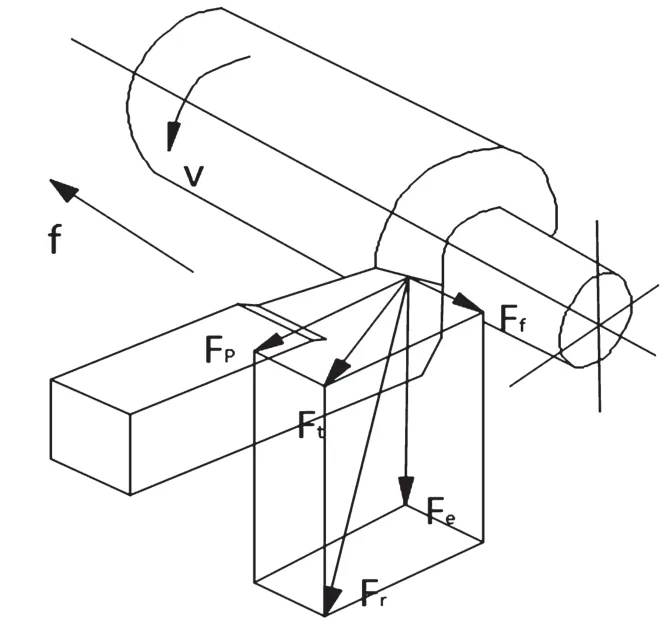
图5 切削力分解图

切削力计算时，常用的经验公式主要有两个，即单位切削力公式和指数公式，本文主要使用指数公式计算切削力。计算切削力指数公式如式（1）～式（3）所示。

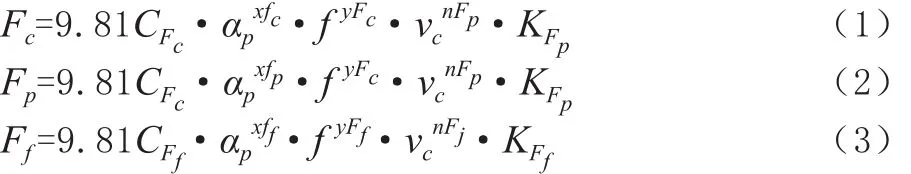
式中：CFc、CFp、CFf为工件材料及切削条件对切削力影响的综合系数；αp为切削深度；f为进给量；vc为切削速度；KFc、KFp、KFf为总修正 系数；xFc、xFp、xFf、yFc、yFp、yFf、nFc、nFp、nFf为工件材料、加工形式和刀具材料对切削力的影响系数。

本文计算时，粗车工况为αp为4mm，f为0.4mm/r，vc为200m/min。刀具为硬质合金刀具，加工刹车盘为灰铸铁材质，计算公式中的系数通过查表具体可得：CFc=903、CFp=530、CFf=451；xFc=1.0、xFp=0.9、xFf=1.0；yFc=0.75、yFp=0.16、yFf=0.5；nFc、nFp、nFf均为 0；KFc、KFp、KFf均为 1.

代 入 式（1） ～ 式（3）， 可 求 得 切 削 力Fc=1816.74kN、Fp=928.27kN、Ff=1250.43kN。

1.3 立柱的静动力学分析

立柱主要受力来源为机床加工时产生的切削力、立柱前段零部件及其自重。通过分析该车床行程图，取机床工作时三种常态，分析立柱静力变形值，结果如表1所示。

表1 三种工况下立柱的变形量

对立柱进行模态分析，机床主轴转速范围为25～2250r/min，因此结构低阶固有频率对其性能影响较大，本文只分析立柱前6阶固有频率[7]。立柱振型如图6所示，振型描述如表二所示。前六阶振型均表现为结构的整体振动，且都为单一摆动或扭转振型，没有局部的振型出现，说明结构整体形式较为合理。

图6 立柱前6阶振型图

表2 立柱前六阶固有频率及振型描述

2 立柱筋板优化设计

2.1 筋板形式选择

元结构是指把机械结构按其组成形体进行分解，从而得到一些几何形状变化不大、结构稳定的基本单元结构。基于元结构优化设计原理，从组成机械结构的单元结构中选择符合机床性能要求及制造工艺的结构，每一个单元结构的动静态性能直接影响机械结构的机械性能，选出最优单元结构作为立柱优化设计的基础结构。

本文根据床身内部的筋板分布特点及常见筋板形式，提取了床身五种单元结构，如表3所示。分析立柱的结构特征，选择单元结构尺寸为600mm×100mm×600mm，单元结构外壁厚度25mm，内部筋板厚度为20mm，材料为HT300。

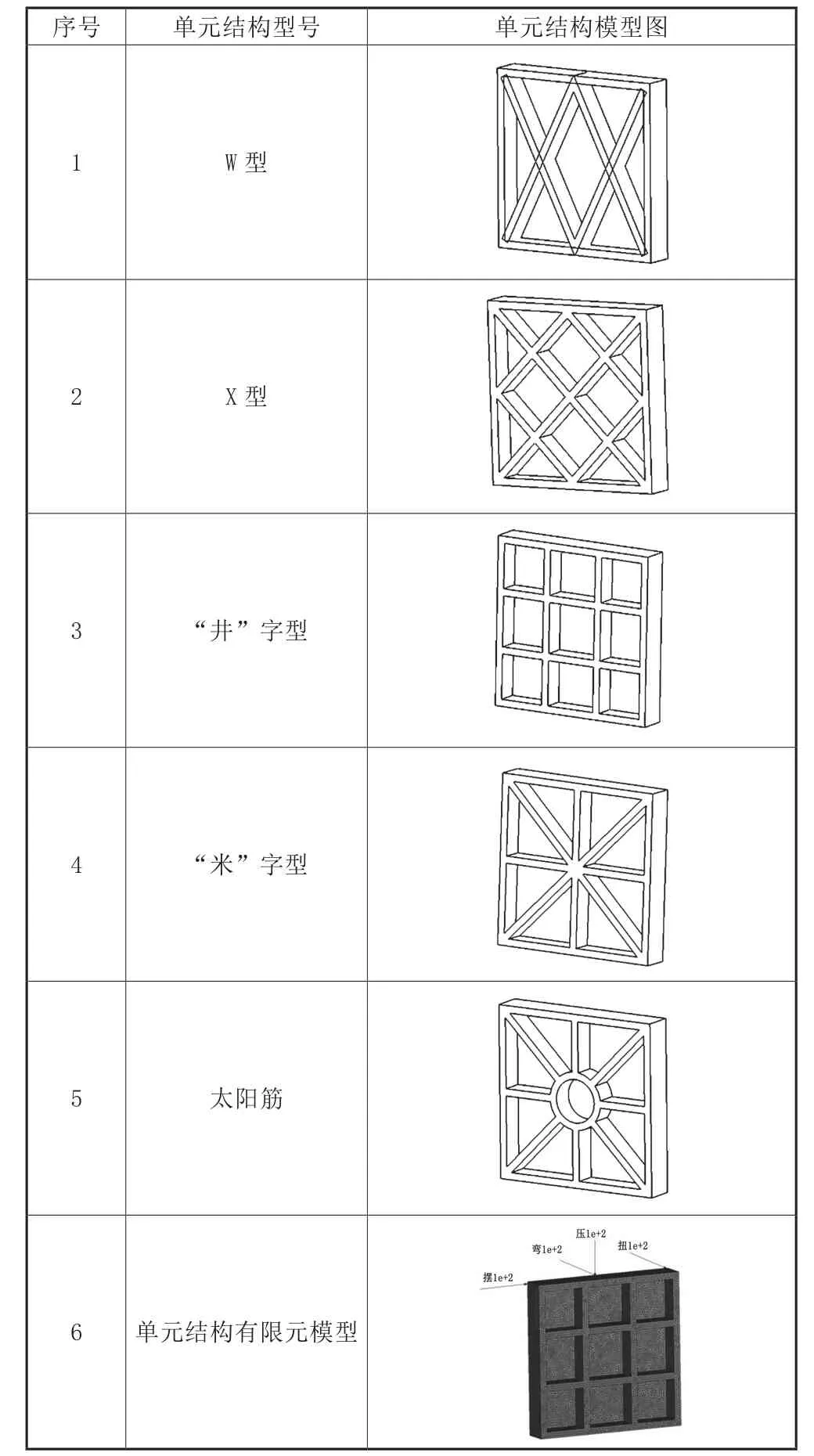
表3 五种单元结构模型图及有限元模型图

筋板单元结构的有限元模型如表3中第6类所示，分别分析5种结构在受压、弯、扭、摆四种工况下的变形情况，考虑材料的影响，各项参数如式（4）、式（5）所示。

式中，Ki表示结构单位体积的刚度值：F为载荷大小；De为载荷作用下元结构变形量；V为元结构体积；Mi表示结构单位体积的固有频率值：M为元结构固有频率，V为元结构体积。Ki值越大，表明单位体积材料的刚度越大，元结构的静态性能越好；Mi值越高，表明单位体积材料固有频率越高，元结构动态性能越好。

五种元结构的Ki、Mi值计算结果分别如表4、表5所示：

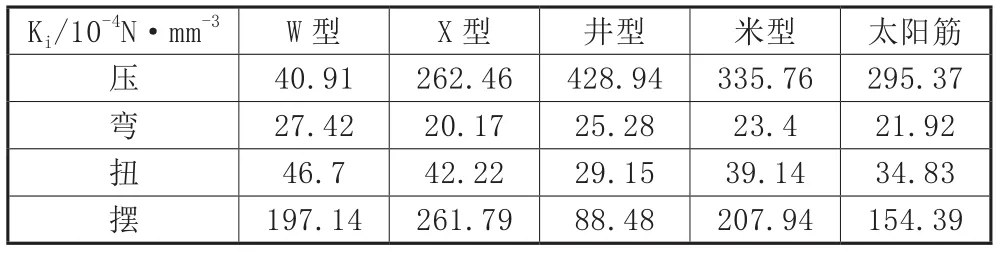
表4 五种元结构Ki值统计表

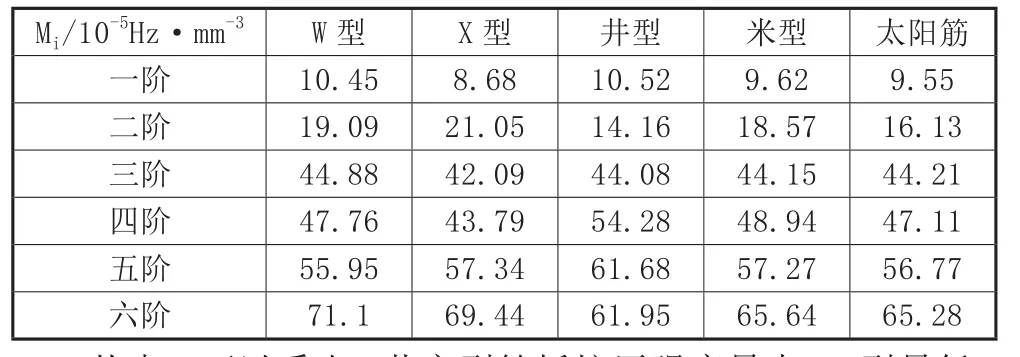
表5 五种元结构Mi值统计表

从表4可以看出，井字型筋板抗压强度最大，W型最低；W型筋板抗弯强度最大，井字型次之，X型最小；W型筋板抗扭强度最大，X型次之，井字型最小；同时X型筋板抗摆强度最大，井字型最小。

从表5中可以看出，井字型筋板是单位体积材料下一阶固有频率最高的，W型筋板次之，X型筋板最低；而二阶固有频率则为X型最高，W型次之，井字型最低。

2.2 立柱筋板的布局

通过对机床实际加工工况进行分析，立柱侧壁面主要承受摆动及扭转载荷，故布置X型筋板。前后壁面主要承受弯曲及扭转载荷，考虑到铸造方便性，布置井字型筋板，同时在立柱底部增加了一圈横筋板，使立柱结构更加完善。改进前后结构如图7、图8所示。

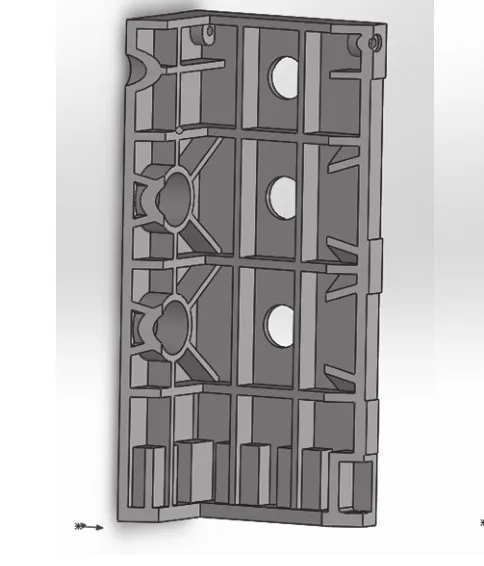
图7 原始立柱筋板结构

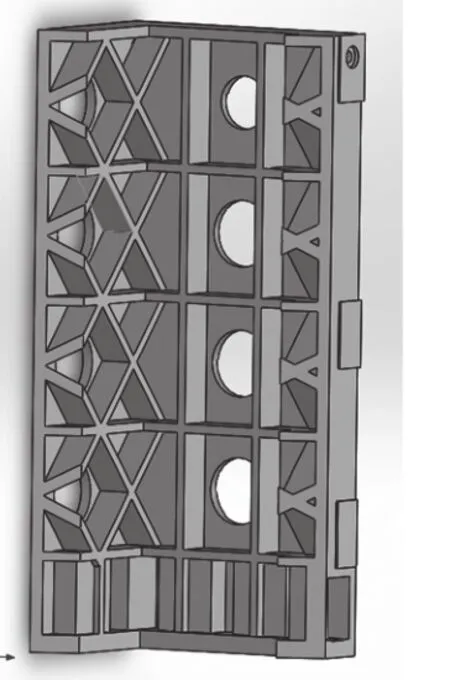
图8 改进型立柱筋板结构

2.3 立柱改进结构分析

对改进型立柱结构进行静力学分析与模态分析，与原始立柱结构的数据对比结果如表6所示。

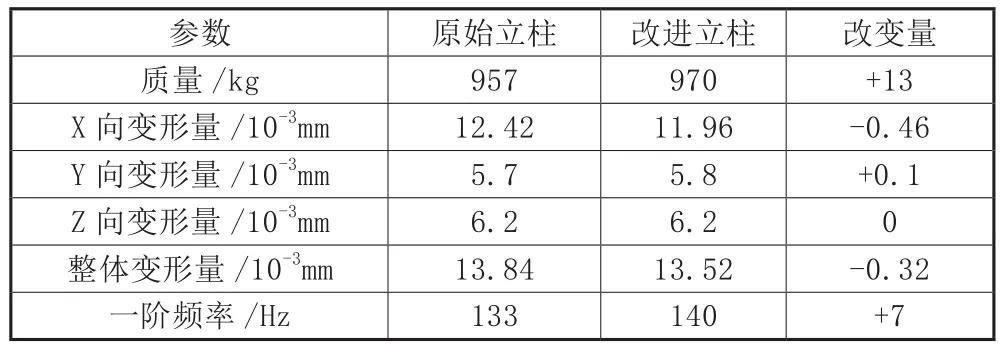
表6 改进型立柱与原始立柱对比结果

从表中可以看出在提高了1.4%质量情况下，立柱变形量减小了2.3%，提升了机床整体静刚度。同时一阶固有频率提升了5.3%，保证了机床的动态性能。

3 结语

本文首先对机床加工时立柱受力情况进行了分析，利用ANSYS Workbench有限元分析软件对立柱进行了静动力特性分析；其次，提取了不同立柱筋板布局的元结构，对不同元结构单位体积材料动静刚度值进行计算，选择满足本文要求的筋板型式；最后，对立柱进行优化设计，重新对立柱筋板进行布置，有效提高了立柱静动力学性能，进一步提升了机床稳定性和加工精度。