城市快速路交织区通行能力分析与仿真

宁波工程学院 浙江 宁波 315031

正文：

0 引言

沿着相当长的路段行驶的两股或多股基本平行的同向交通流，不借助于交通控制设施运行，定义为交织。并且交织区交通流特性对于公路以及城市快速路合流以及分流区域的瓶颈消除有着至关重要的作用。其具体概念为当道路由合流区入口、辅助车道、分流区出口紧密相接时，或者当一条驶入匝道、一段辅助车道、一条驶出匝道紧密连接时，这两种构成形式就形成了交织区。

由于交织区较基本路段相比较复杂，影响其通行能力因素众多，以1950年美国《通行能力手册》的发布拉开了学者们研究交织区的帷幕。HCM2000将交织区构型分成A、B、C三类，给出了在交织区构型、长度、车道数和流量比在不同情况下组合时的通行能力值。Lertworawanich等利用线性规划理论来求解交织区通行能力。我国交通部门将交织区分成Ⅰ类、Ⅱ类、Ⅲ类，通过各种因素对交织区运行特性的影响分析，建立了其通行能力模型。任荔娜根据城市快速路车辆的动态运行规律，得到了交织区内车辆的行为特征及交通流特性，并依据此特征建立了基于元胞自动机的城市快速路交织区跟驰模型及换道模型。蔡雯娟通过定性和定量相结合的方法，分析交织区各个参数的分布规律并建立VISSIM模型，最终推算出设计车速为80km/h时的符合我国西安市驾驶员特征的城市快速路A类三车道交织区通行能力计算公式。

若直接采用实地调查的方式来建立模型，则需要大量的人力物力投入，且受到资金、技术等限制，而在模拟仿真中，交通流参数都是人为输入设定，有时得出的结论与实际背道而驰。因而，本文利用VISSIM模型对交织路段进行仿真实验，将理论模型所得出的数据与部分实测数据相结合，通过改变其输入条件，将各种情况排列组合，得出在不同情况下的通行能力值，确立交织区通行能力模型，最后用宁波市区机场南路交织路段验证此模型的准确性。

1 交织区通行能力影响因素

交织区在道路通行系统中占有重要地位，本文主要研究交织长度，交织车道数，交织区构型，交织流量比四个因素对通行能力的影响。

1.1 交织区长度

主路与匝道车辆在行驶过程交汇并变换一次车道行驶的距离称为交织区长度。HCM2000认为，高速公路一般交织区长度应该在750m以下，由于其车辆类型以及属性、行车类型均不同，所有城市快速路限速和长度一般低于高速公路。本文所研究的交织区长度为500m，对大多数城市快速路交织区来说，此长度下的通行能力较有借鉴意义。

1.2 交织车道数

交织车道数，即交织区段内的车道数，是供车辆完成交织行为的附加车道，一般用N表示。A类交织区中能被交织车辆使用的最大车道数是受限制的，每辆车最多使用车道数约为1.4个车道。我们一般都用车道数来衡量一条道路的通行能力，通常在其他影响因素都适宜的条件下，车道数越多代表通行能力越强，所以交织车道数可以作为影响交织区通行能力的一个重要影响因素。

1.3 交织区构型

交织区构型主要有A、B、C三类，A类交织区中两个交织方向的所有车辆均进行一次变换车道行为;B类交织区是最主要的交织构型，可以有效承载较大交织交通量；C类交织区与B类较为相似，仅较于B类多一条直通车道。本文主要讨论了A类交织区构型的通行能力。

1.4 交织流量比

交织流量比为交织流量与总交通量的比值。车辆在交织区中运行过程中存在交织行为，导致交织区内交通流车头时距增加，导致交织区通行能力会比一般路段的通行能力小。因此，交织流量比是影响交织区通行能力的重要因素，有着举足轻重的地位。

2 确定交织区通行能力模型

2.1 确定模型

由于城市快速路交织区长度大多均为500m，为了得出交织流量比与交织通行能力的关系，根据通行能力与交织区流量比的关系，采用当交织流量比为0.2、0.25、0.3、0.35、0.4时500米A类交织通行能力，并做出如下假设模型：

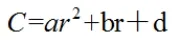
其中：C-----交织区通行能力

r-----交织流量比

a，b，d-----标定参数

3.利用VISSIM仿真

本节利用基于Vissim搭建的仿真平台，构建通用A型交织区仿真路网进行仿真；在城市快速路交织区通行特性的基础上标定仿真参数；基于以上两点来得出仿真结果再由matlab进行数据趋势拟合，与理论的模型进行对比分析，验证理论模型的正确性。

3.1 仿真背景介绍

选取A类快速路交织区一般典型路段作为仿真实验路段，该路段有一个交织区，由一个入口匝道和一个出口匝道构成，如图3-1所示。该实验路段交织区设定车道数为变量，主入进口车道数从两车道开始变化，入口匝道与出口匝道数从单车道开始变化，实验交织区长度作为变量将设置200米到500米作为变化范围。

图3-1 A类交织区仿真路网

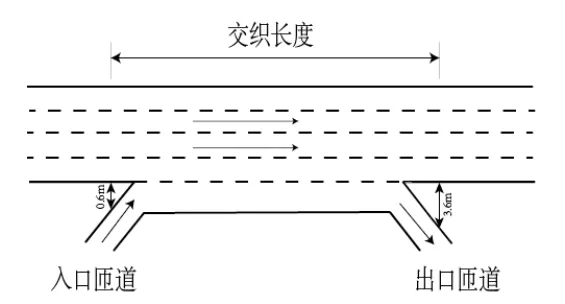
图3-2 交织区路段示意图

3.2 仿真软件参数标定

1.仿真参数设置：本次仿真时间设置为1h，所以将VISSIM中仿真参数设置为3600仿真秒，考虑实际条件，将仿真精度设置为5，根据仿真经验将随机种子设置为42。

2.驾驶行为参数设置：①由于快速路交织区比其他路段更易发生交通问题，交通冲突较其他路段更多，所以应该将驾驶人的最大前视距离设置应由原本的250米增加到257米。②由于快速路交织区的车道变换相比于其他路段更加复杂，在VISSIM软件内不加设置会导致车辆集中堵在下半段区域，所以需要对车辆车道变换模型进行修正，具体设置结果如图3-3所示。

图3-3 车道变换模型修正

3.变道位置设置：在输入车辆后，经过多次仿真，发现未经设置时的车辆变道常发生在交织区下半部分（如图3-4所示），与实际不符，实际调查中车辆变换应该大都发生在交织区前半段所以应该对车道变换距离进行更改。本次仿真将交织区下游的路段连接器的车道变换距离均修改为250m，紧急停车距离修改为10m。

图3-4 初始仿真交织区变道位置图

经过以上参数标定后，虽然无法做到与实际完全等同，但是比之前更加接近与实际情况，更加真实，使得车辆变道更合理有序。

3.3 仿真数据标定系数

在2、3、4车道情况下分别进行五组不同交织流量比的仿真，并得出相应的15组通行能力数据（如表3-1所示），将数据用于模型的系数标定，得出相应的系数。将上表数据引入模型，并标定系数：

表3-1不同交织流量比对应通行能力数据

其中：C —— 交织区通行能力

r —— 交织流量比

3.4 实测数据检验

根据宁波市机场路夏禹路立交北侧的快速路交织区来验证模型的适用性，其长度约500m，交织流量比2.5：7.5，车道数为3，并将这些参数输入通行能力计算模型，可得通行能力计算结果为3993pcu/h，实际观测值与模型得出的通行能力相差不超过5%，因此此通行能力计算模型是有适用性的。

4.结论

本文以典型A类快速路交织区为例，基于假定模型，运用Vissim软件进行快速路交织区的仿真模拟，得到快速路交织区的通行能力并进行分析，得到如下结论：

(1)通过假设交织区通行能力模型，通过VISSIM仿真进行参数标定，分别得到2、3、4车道数下的三种通行能力模型，该模型能更好的模拟实际的交通状况。

(2)对A类交织区进行VISSIM仿真模拟，在不同车道数下VR对该类交织区通行能力的影响进行分析。利用Matlab分别对车道数为2、3、4，交织长度为500m的情况进行拟合，获得不同情况下的城市快速路交织区通行能力模型度。

(3)通过VISSIM仿真模拟，可以反映交织区的通行特性，通过仿真数据与实际数据相比较，认为该模型是具有一定的可行性与适用性的，拥有良好的实用价值。