通过情境提出问题 利用问题串 引发思考
杨帆
【摘要】 正确理解数学概念是学生学会数学的基础,因此,如何生成数学概念在数学概念教学中有着举足轻重的作用.本文以“函数单调性”案例为素材,从学生认知规律出发,探讨了如何设计问题串,创设情境,使得数学概念有效生成,从而逐步加深学生对概念的理解和应用.
【关键词】 概念教学;问题;情境
概念教学的重点在于概念的生成过程,在于关注学生的思维过程.一个好的数学概念教学设计应该能够激发学生学习兴趣,使学生经历概念生成过程,并使其能够概括概念并学会应用概念解决问题.合理地设计问题情境,能够激发学生的学习兴趣和学习动机,以积极的态度主动探索领悟,促成概念的生成.在一次南京市级公开课中,笔者准备的“函数单调性”受到好评.本文以“函数单调性”的教学设计为载体,浅谈如何设计“问题串”,创设情境来优化数学概念教学.
一、课堂实录
(一)创设情境,引入课题
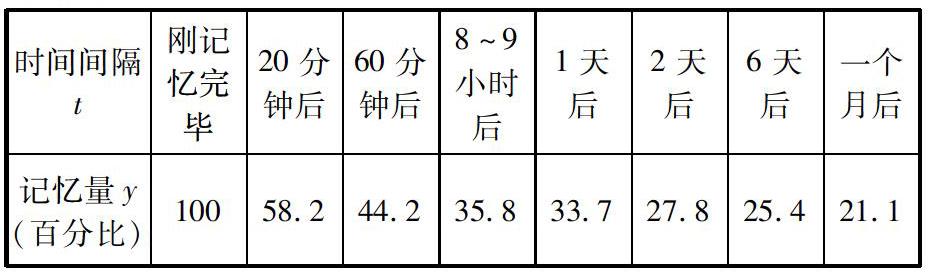
德国有一位著名的心理学家艾宾浩斯,对人类的记忆牢固程度进行了有关研究.他经过测试,得到了以下一些数据:
时间间隔t 刚记忆完毕 20分钟后 60分钟后 8~9小时后 1天后 2天后 6天后 一个月后
记忆量y(百分比) 100 58.2 44.2 35.8 33.7 27.8 25.4 21.1
[问题1]这张表反映了什么问题?
[问题2]能不能用函数的观点来分析一下这张表.这里有没有函数关系的存在?
[问题3]谁是谁的函数?
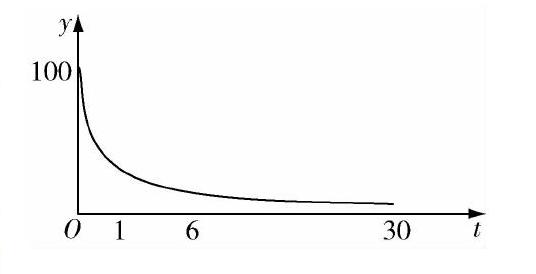
[问题4]从图像的走向来看,我们怎样用图形语言来判断记忆量是在增大还是在减小呢?
设计意图:通过问题串的形式,使学生从表格中抽象出数学中所研究的函数图像.引导学生用图形语言来判断记忆量随时间间隔的变化情况,通过直观感受,学生了解了函数图像上升就是记忆量增加,反之就是记忆量减少.
(二)創设情境,启发定义
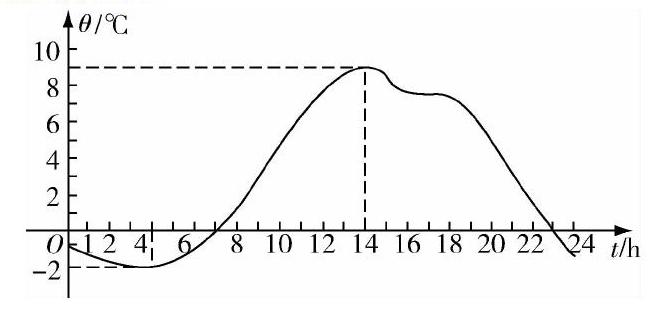
情境:某一天的温度θ关于时间t的函数θ=f(t),t∈[0,24]的图像如下.
[问题5]图像是一直上升或下降的吗?怎样用图形语言描述气温随时间的变化情况?
[问题6]在区间[4,14],函数图像呈什么趋势变化?
[问题7]怎样用数学语言来刻画在[4,14]这个区间,气温随着时间的升高而升高这个特征?
师生活动:学生进行分组探究,给出方案,师生共同讨论研究.
生1:能不能在区间[4,14]上取两个端点值4,14,4<14,若4所对应的函数值f(4)小于14所对应的函数值 f(14) ,就可以说明在[4,14]上,气温随着t的增大而增大?
师:大家觉得他的方案可不可行?讨论一下.
生2:不可行,图像有可能不是一直上升的.
师:那能不能取三个点,例如,4<10<14,有f(4)< f(10)< f(14),是不是就可以说明在[4,14]上,气温随着时间的增大而增大?
生:不可以.应该取无数个点.
师:如果有无数个点在依次增大,这无数个点所对应的函数值也在依次增大,那是不是就可以说,在[4,14]上,气温随着时间的增大在增大,也就是说在[4,14]上,从左往右看,图像一直呈上升趋势?
生:不是,有一个点不满足都不可以.
师:那我们应该怎样取点?
生:取遍区间每一个点,即任意取点.
设计意图:通过提出用数学语言刻画函数图像上升趋势的问题,引发学生思考.使学生感悟由形到数的翻译,由直观到抽象的转变.师生共同合作探究,逐步加深学生对“任意”的理解,使学生学会用数学语言来刻画函数图像上升或下降的趋势,为引出函数单调性概念做铺垫.
(三)认识定义,巩固深化
[问题8]请你给“函数单调性”下个定义.
师生活动:辨析定义,提出能用“所有”与“无数”替换“任意”吗?能将“区间I”换成“定义域”吗,进一步认识定义.
设计意图:通过对关键词“任意”“区间”“都有”的分析,让学生深刻体会到“无数”并不等价于“所有”,函数的单调性是对定义域内某个区间而言的,它反映的是函数的局部性质.从学生已有的认知结构出发,帮助学生形成良好的概念网络,由学生自主概括概念.
(四)例题讲解,巩固新知
例1 画出下列函数的图像,并写出单调区间.
(1)y=-x2+2;
(2)y= 1 x .
思考:可不可以说y= 1 x 这个函数在整个定义域上是单调减函数?
师生活动:学生讨论探究,举反例示范,并引导学生进行归纳.
设计意图:通过问题引发学生思考,使学生更加透彻理解函数在某个区间上是单调增函数(或减函数),但是在整个定义域上不一定是单调增函数(或减函数).
思考:我们可以根据函数来确定单调区间,函数图像带给我们的是直观的感觉,能不能用数学符号语言对你所形成的结论加以证明呢?
例2 证明函数y= 1 x 在(0,+∞)上是减函数.
设计意图:通过定义证明函数单调性,教师板书演示,使学生了解如何用数学语言来严谨地证明函数单调性.让学生感受数学概念的严谨性.
(五)小结回授,感悟数学
[问题9]本节课你学会了用哪些语言来描述函数的单调性?试用自己理解的语言叙述.
[问题10]这节课我们学习了哪些数学思想方法?
设计意图:以问题讨论的方式进行小结,培养学生反思的习惯,鼓励学生运用自己理解的语言对问题进行质疑和概括.抓住概念本质,体现概念升华.
二、教后反思
(一)合理创设情境,激发学生求知欲,促进概念生成
1.创设的情境要直观,体会概念源头
直观的情境,能够使学生更好地进行思考和训练,激发学生学习兴趣,体会概念的源头.例如,本文中采取的艾宾浩斯遗忘曲线和温度变化图两个情境,均以图形的方式展示给学生,加深学生的直观感受,促使学生更容易地用图形语言来形容图像的变化趋势,为后面更好地生成概念做铺垫.
2.创设的情境要有趣味性,加深概念理解
有趣的问题情境不仅能激发学生求知欲和学习兴趣,而且能够加强师生的情感交流,为数学概念教学打下基础.例如,本文中的艾宾浩斯遗忘曲线情境,在上课初始抓住学生兴趣,调动学生自主探索研究,在学生学会自主概括单调性概念以后再回头解决开始的遗忘曲线情境问题,加深单调性概念的理解.
(二)注重问题建设,设计有效“问题串”,加深数学概念理解
1.应当设计阶梯性“问题串”
数学概念有一定的抽象性,学生很难把握重点、难点,设计阶梯性“问题串”,有利于引导学生层层分析、由浅入深、循序渐进,更好地理解数学概念.例如,本文中问题1到4,使学生更好地理解了如何用图形语言来描述图像趋势.问题5到7,使学生逐步学会了用数学语言严谨地刻画图像趋势.
2.应当设计符合学情的“问题串”
要设计以学生为主体的“问题串”,贴近学生实际.以学生已有知识、经验、能力为基础设计的问题,符合学生的认知规律,才能促进知识的同化,才能全面地理解概念的内涵和外延.
高中数学课程指出:“高中数学课程应该返璞归真,努力揭示数学概念、法则、结论的发展过程和本质,把数学的学术形态转化为学生易于接受的教育形态.”所以我们在设计数学概念课时,一定要遵循学生认知规律,合理地设计问题情境,重视概念的形成和发展过程,努力揭示数学本质,使概念教学切实有效.

