一类奇异三阶常微分方程m点边值问题正解的存在性

刘慧

（南京财经大学应用数学学院, 江苏 南京 210023）

常微分方程边值问题的研究有着悠久的历史，其相关理论可以追溯到牛顿和莱布尼兹建立微积分学的最初阶段。最近几十年常微分方程边值问题的研究发展迅速，马如云[1]介绍了二阶常微分方程多点边值问题的正解存在性，此后又有许多学者[2-14]讨论了三阶或四阶常微分方程多点边值问题的正解存在性。常微分方程边值问题主要应用于化工、水流动、热传导、热弹性、血浆流动等多个领域，研究边值问题常用的方法有上下解方法[7-8]、打靶法[9]、单调迭代理论[10]、不动点指数[11-12]，以及各类不动点定理，如 Krasnoselskill 不动点定理[4,13]和Leggett-Williams 不动点定理[14]。

三阶常微分方程边值问题解的存在性在科学技术和生产实践中有着更加重要的实际意义。吴红萍[14]利用 Williams-Leggett不动点定理讨论了非线性三阶三点边值问题得到了至少三个正解的存在性；程德胜[2]运用锥拉伸与压缩不动点定理对一个含参数的三阶三点边值问题在满足超线性或者次线性条件下正解的存在性进行了探究；郭丽君[12]用不动点指数理论得到了一类三阶三点边值问题至少两个正解的若干存在性准则；高婷[13]研究了下面奇异三阶m点边值问题

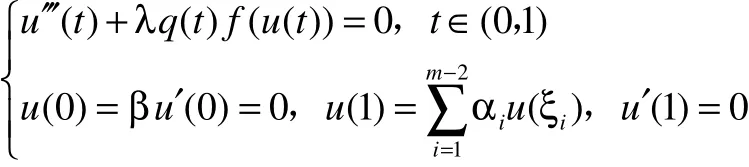
在f满足超线性或次线性的情况下，运用锥拉伸与压缩不动点定理得到了问题正解的存在性；许洁[15]通过与一个线性算子相关的第一特征值的讨论，运用不动点指数定理得到了以下边值问题

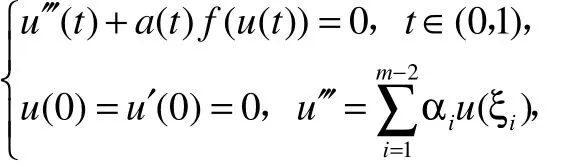
正解存在的结果。

受上述研究内容启发，本文主要研究和文献[15]相同的一类奇异三阶常微分方程m点边值问题

的正解存在性,其中αi≥0,i=1,2,…,m-3,αm-2≥0 且α在0,1 处奇异,ξi∈(0,1)满足 0＜ξ1＜ξ2＜…＜ξm-2＜1。

本文给出了Green函数的另外一种简单的表示形式，并得到了新的性质，最后在f满足超线性或者次线性的条件下运用Krasnoselskill不动点定理研究BVP（1）、（2）的正解存在性。

本文假定以下条件成立：

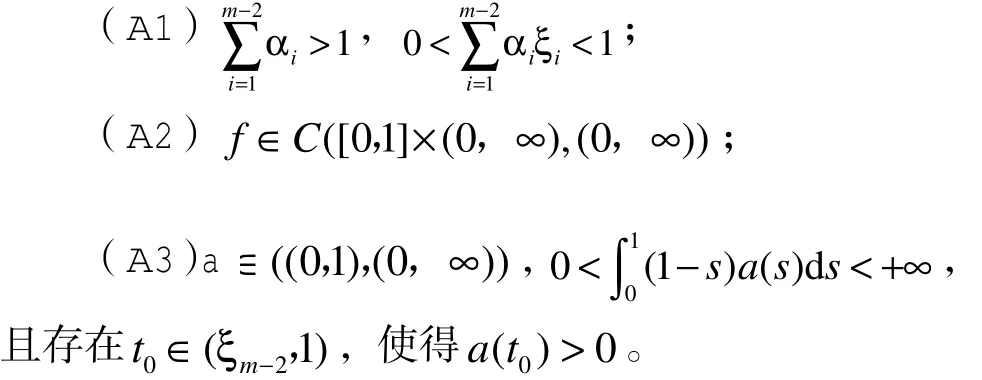
1 预备引理

引理 1（Krasnoselskill不动点定理）：设 E是Banach空间，K⊂E是E中的一个锥。Ω1和Ω2是E的开子集，若全连续算子

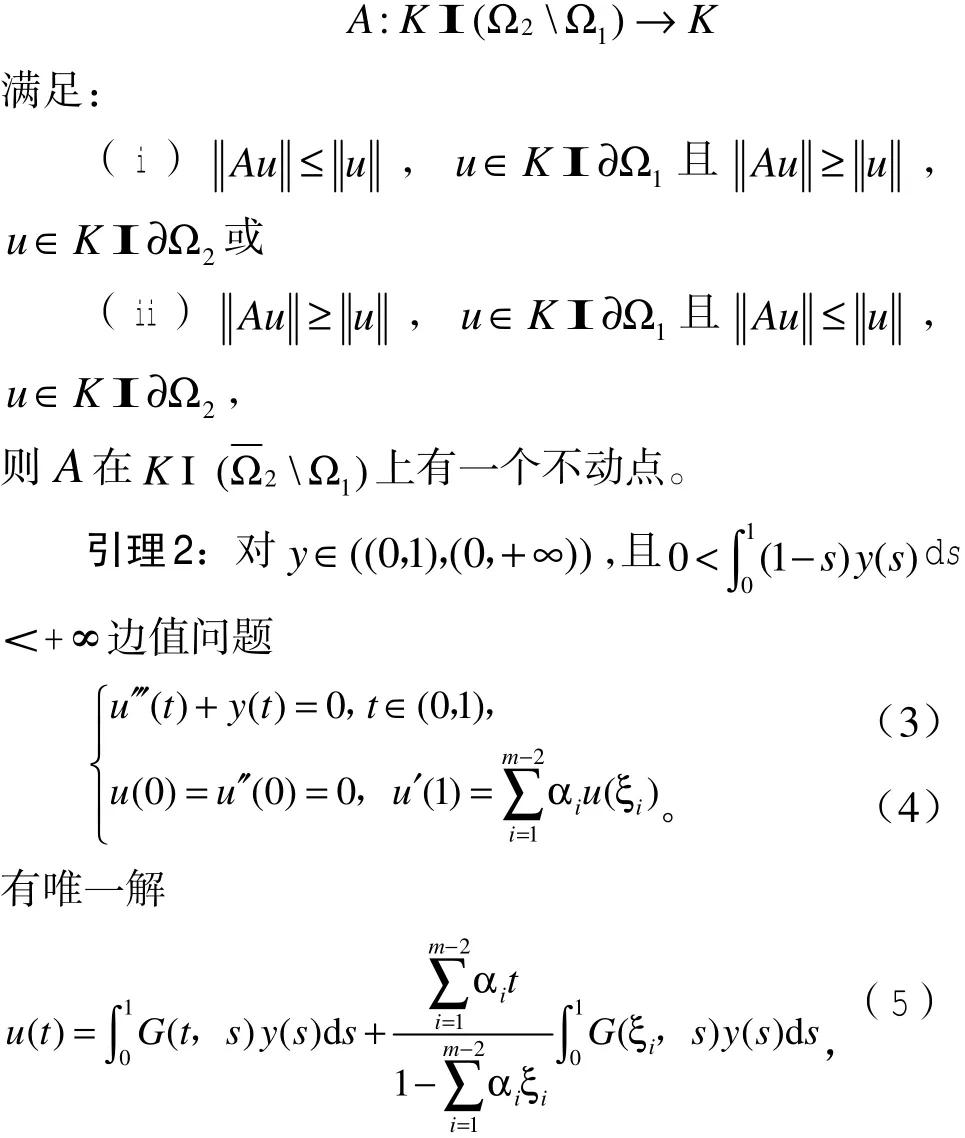
式（5）中

结合边值条件可得到

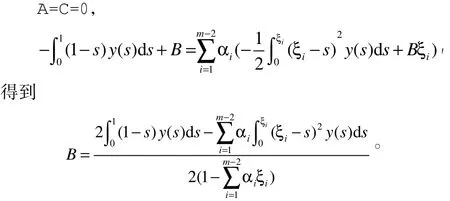
带入有：

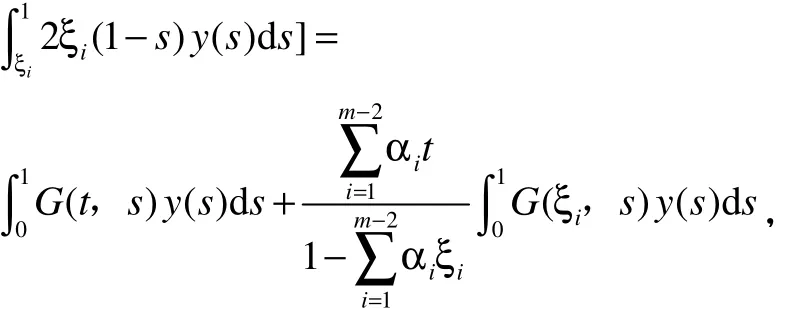
引理2得证。

证明：(1)当st≤时，

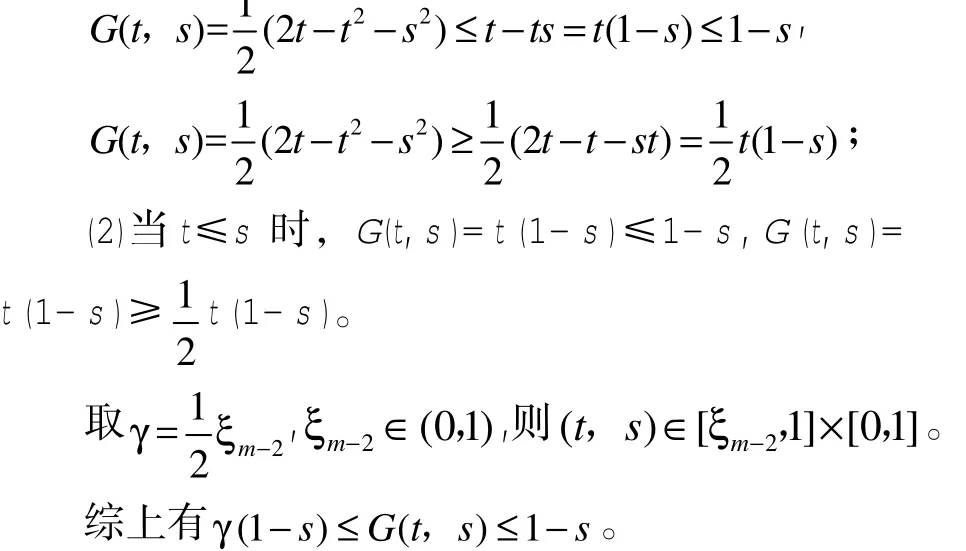
引理3得证。

引理 4：设（A1）成立，y ∈ C((0，1)，(0， + ∞ ))，且 y ≥0则边值问题（3）、（4）的唯一解u满足：

这里γ如引理2定义。

2 主要结果

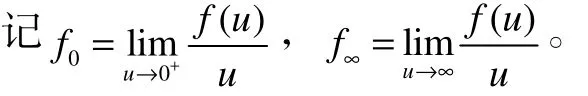
定理1：设（A1）—（A3）成立。设 f满足下列两个条件之一：

（i）00f= ， f∞=∞ (超线性)；

（ii）0f=∞，00f= (次线性)。则BVP（1）、（2）至少有一个正解。

下面运用上述4个引理证明定理1。

根据引理2，BVP（1）、（2）有解 ()u u t= ，当且仅当u是算子方程

的解。

假设

规定它的范数

则E是一个Banach空间。

定义

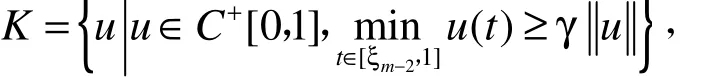
则K是E的一个锥，且由引理3知AK⊂K且易知

A: K→K是全连续算子。

超线性情形： f0= 0 ，f∞=∞。

首先，由 f0= 0 ，可选取 H1> 0 使得 0 < u < H1时，f( u)≤εu，其中ε>0满足：

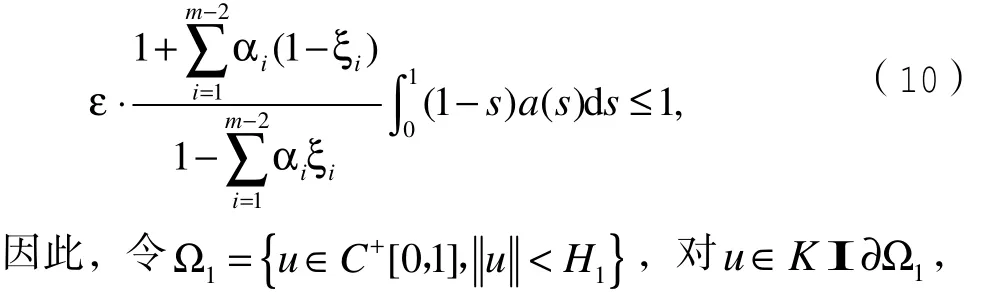
由式(8)和(10)有

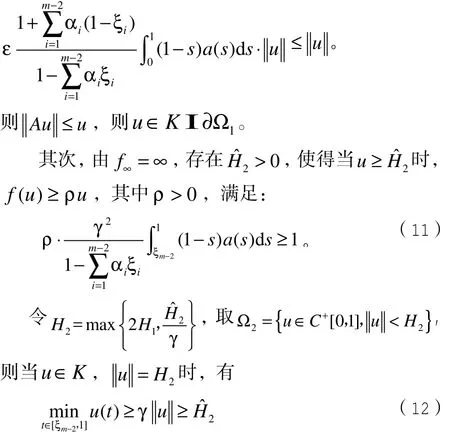
和

根据引理1的第一部分, A在KI(Ω2Ω1)上有一个不动点u满足 H1≤u≤H2。从而定理1在超线性情形下得证，下面证明次线性情形。

次线性情形： f0=∞, f∞= 0 。

首先，由 f0=∞，取 H3> 0 使得当 0 < u < H3，f( u)≥Mu。其中M满足

其 次, f∞= 0 ,故 存 在 Hˆ4> 0 ,使 得 当 u ≥ Hˆ4时,f( u)≤λu,其中λ>0满足：

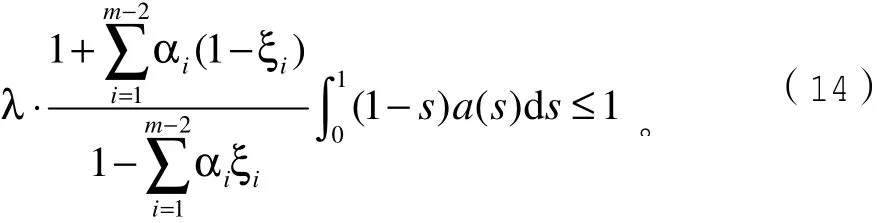
分以下两种情况考虑：

情形1：f有界。即存在N，有()f uN≤。

取

情形2 ：f无界。

综上，定理1得证。

3 结语

（1）本文研究的三阶m点边值与文献[15]研究的边值条件相同，但是本文运用的是Krasnoselskill不动点定理，而文献[15]运用的是不动点指数定理。

（2）本文给出了Green函数的另外一种简单的表示形式，以及选择了一个适当的锥且在f满足超线性或者次线性的条件下得到了该类奇异三阶m点边值问题的正解存在性，而文献[15]是通过与一个线性算子相关的第一特征值的讨论得到了该问题正解的存在性。