基于新改进的SVM不平衡数据集分类算法
刘悦婷,李晓霞,李思璇,朱旭博
(兰州文理学院传媒工程学院,甘肃 兰州 730000)
分类是对输入训练样本分析、学习后得到决策模型,然后预测未知样本,它已成为机器学习领域的重要研究方向。目前,已有众多经典算法可以实现平衡数据的良好分类效果,如支持向量机法、模糊分类算法、代价敏感学习法和决策树算法等[1]。但是,现实中许多应用领域存在明显的不均衡数据,如网络入侵、商业欺诈、文本分类等数据集[2-3],人们很重视少数类的信息。在分类判决时,传统分类器总会偏向多数类,把少数类分到多数类,导致错分率很高,分类器性能不理想[4]。因此,如何提高不平衡数据的分类性能已成为众多学者研究的热点[5]。
目前,不平衡数据分类的方法主要从数据层面和算法层面实现。数据层面完成数据预处理,包括欠采样、过采样和混合采样。欠采样是通过减少多数类样本使数据集均衡,可能造成信息丢失,降低分类器的性能[6-7]。过采样是通过复制、插值增加少数类样本使数据集均衡,但会造成过拟合,增加分类器的空间和时间消耗[8-9]。混合采样是将欠采样和过采样有效结合从而平衡数据集的分布。
算法层面是对分类算法本身进行操作,包括对传统算法的改进、众多算法的集成等。改进算法主要通过调整分类边界、改变概率密度等措施修改算法在数据集上的偏置,使得决策面偏向于少数类,提高少数类的分类性能[10]。Wang Chinheng等[11]提出先由 SVM(Support Vector Machines)确定近邻数目,再由 KNN(K-Nearest Neighbors)算法完成分类;王超学等[12]提出 WSVM(WeightTechnologyandbasedgrading Support Vector Machines)算法,按照聚类权重定性选择出对分类决策面起作用大小的多数样本,将选取的多数类样本与少数类完成SVM组织训练。文献[12-13]提出不平衡数据集的特点:两类数据数量差别很大,类分布比较均匀;两类数据数量相当,但类分布差别较大,如一类比较集中,一类比较分散;两类数据数量和类分布差别都很大。传统分类方法都是基于第一种情况的研究,对后面两种情况不适用。杨扬、李善平[14]提出基于实例重要性的方法解决不平衡数据分类问题,但忽略了类内不均匀对分类精度的影响。
受文献[13-14]的启发,本文提出基于样本密度的平衡法,依据多数类每个样本在距离临界区域内的密度值思选择出对分类决策面起作用大小的样本,将训练集按照样本作用大小分别与相同数目的少数类结合进行重新组织训练,通过实验将本文方法与 ALSMOTE-SVM、WSVM算法和 SVM算法完成了比较,验证了本文算法的优越性。
1 SVM算法
基于统计学习理论的SVM是建立在结构风险最小化原理上,寻求最优分类面。对于原始特征空间中不可分的问题,通过核函数映射到更高维的特征空间中,转化为求解线性约束的二次规划问题。

构造SVM优化模型

为求解式(2)二次规划问题,构造lagrange函数
式(3)分别对 求偏导,并置零,得到式(2)的对偶问题


求得判别函数为


2 基于新改进的SVM算法(IMSVM)
2.1 问题分析
现实中许多不平衡数据集具有分布不均匀,类间边界模糊等特点,或者在数据空间不同区域具有不同的密度,导致传统分类算法难以实现理想的结果。通过图1数据集说明密度不均匀问题,图1数据集中,a、b、c分别代表3个簇所在的范围,由图 1知密度关系a>b>c,传统的分类算法很难找到统一的邻域半径来发现3个类别a、b、c。若邻域半径取值较大,a和b容易被认定为一个类;反之c被视为噪声。要解决该问题,简单方法是人为设定邻域半径值,然而在数据集密度分布情况未知的情况下,人为设定邻域半径值有很大的难度,因此对分布不均匀数据集的正确分类造成很大困难。
一般来说,想得到整个数据集密度分布情况十分困难,所以本文算法考虑通过样本的密度值确定样本所在的区域。而样本的密度值可通过统计距离临界区域包含的样本个数来得到,样本个数越多,密度越大,说明样本间越密集,样本所在区域接近簇类中心;反之,样本个数越少,密度越小,样本间越稀疏,样本所在区域接近类边界。边界区域密度值最小,很容易发生错分,严重影响分类精度,因而对分类结果“作用最大”。靠近边界的样本是单例数据或有助于克服噪声数据的影响,因而对分类结果“作用较大”,其余区域的样本对分类结果“作用较小”。因此采用距离临界区域内样本个数来标识样本的密度信息,从而判定样本在类的区域。
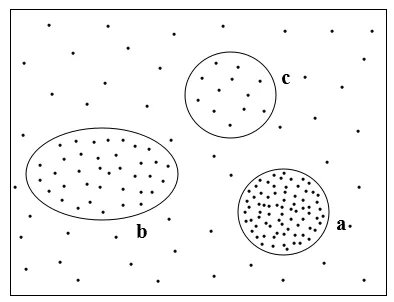
图1 不平衡数据集Fig.1 Imbalanced dataset
2.2 样本的密度值
给定包含 维、 个样本的数据集 ,样本 到样本 ( ∈ 、∈ )的欧氏距离为式(8)。

定义:样本距离临界区域的密度值。样本 距离临界区域的密度值 义为

的距离小于等于 的样本个数,即以 为中心,到 的距离小于等于 的样本数目。
2.3 本文算法流程
本文提出一种新改进的SVM不平衡数据集分类算法。该算法先计算每个样本在距离临界区域内的密度值,再根据密度值的大小分别选出多数类边界区域、靠近边界区域的样本,并且所选样本数目与少数类数目相同,保证样本的均衡性。对分类结果“作用最大”的是多数类的边界区域的样本,对分类结果“作用较大”的是靠近边界区域的样本,对分类结果“作用较小”的是剩余区域的样本。因此,先从多数类样本中选取与少数类数目相等的密度值最小、次最小的两部分样本,再将选取样本分别与少数类样本完成SVM初始分类,从而保证训练样本数量的平衡性,最后用所得支持向量机和剩余的多数类样本对初始分类器迭代优化训练。
IMSVM算法的流程为:
Step1:初始化变量。 少数类样本集合, 少数类样本总数; 多数类样本集合,多数类样本总数;order多数类样本按密度值降序排列的集合;order_behind是order集合中最后 个样本组成的集合;order_behindf是order集合中次最后 个样本组成的集合;order_other是order集合中剩余样本组成的集合。
Step2:对于训练样本,分离出多数类样本集合。
Step3:从集合 中任选样本 ,用式(9)计算样本距离临界区域的密度值。依次类推,计算集合N中所有样本的密度值,以密度值降序排列集合 中的所有样本,得到集合order。
Step4:判断 的关系。若 < ≤2 ,可认为训练样本是平衡样本,用传统SVM训练样本,得到分类结果;若 >2 ,可认为是不平衡样本,转入Step5。
Step5:集合P和order_behind组成的两类平衡集合PN1,用PN1训练 SVM,得到支持向量机PN1,多数类支持向量个数neg1,少数类支持向量个数npos1。
Step6:集合P和order_behindf组成的两类平衡集合PN2,用PN2训练 SVM,得到支持向量机PN2,多数类支持向量个数neg2,少数类支持向量个数pos2。
Step7:在不影响分类精度的同时,使用支持向量集取代训练样本集进行训练可以降低训练时间。由支持向量机PN1、PN2和order_other组成集合 MPN3,从
PN3中提取全部支持向量(pos1+pos2+neg1+neg2)个,提取与支持向量相同数目的多数类,完成SVM分类器迭代训练,并完成支持向量的更新。当满足式(10)的 <0.9时,返回到 Step4执行;当满足 ≥0.9时,迭代训练停止,输出分类结果。

3 实验分析
3.1 评价指标
针对不均衡数据集的特点,传统分类器的性能指标存在严重的缺陷。经研究学者们提出以下指标[15]:不均衡数据集中少数类别的样本为正类 ,多数类别的样本为负类 ,其中,
TP:实际为正类被预测为正类的样本个数;
FN:实际为正类被预测为负类的样本个数;
FP:实际为负类被预测为正类的样本个数;
TN:实际为负类被预测为负类的样本个数。
(1)查全率:少数类样本的正确率。

(2)特异度:多数类样本的正确率。

(3)查准率:被正确分类的正类样本占被分为正类的全部样本比值。
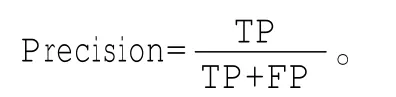
(4)G-mean:综合考虑少数类和多数类两类样本的分类性能,若分类器分类偏向于某一类,则会影响另一类的分类正确率。

(5)F-measure:是查全率和查准率两个评价方式的结合,能有效反应分类器对少数类样本分类性能的敏感程度。

(6)AUC:计算 ROC(Receiver Operating Characteristic)曲线下的面积作为不平衡数据的评价方式,它能全面地描述分类器在不同判决阈值时的性能。
3.2 各算法实验结果比较
为验证本文算法的可行性,用Matlab2014a编写程序,选人工数据集Dataset和UCI数据集为实验对象,将测试结果与文献[9]ALSMOTE-SVM(Active Learning Smote Support Vector Machines)、文献[12]WSVM算法和SVM算法比较。
图2所示Dataset是密度不均匀的人造数据集,包含1018个数据点。
从UCI库中选取不平衡较轻Iris、Glass Identification数据集和高不平衡率Spectf Heart、Ecoli数据集进行实验,如表1所示。
SVM分类器参数设置为选取高斯函数为核函数,参数取值如表2所示,实验迭代运行20次,4种算法在5个数据集上运行得到G-mean、F-measure和CPU运行时间(表 3)。
在人工数据集 Dataset、GlassIdentification和Spectf Heart上运行4种算法,得AUC变化曲线分别如图3-5所示。

图2 人工数据集DatasetFig.2 Artificial dataset

表1 实验数据集Tab.1 Experimental dataset

表2 参数取值Tab.2 Parameter value

表3 实验结果比较Tab.3 Comparison of experimental results
由表3可知:
(1)对于不平衡性较轻的 Glass Identification、Iris数据集,每个样本成为支持向量的可能性较大,故本文算法较 ALSMOTE-SVM、WSVM算法在 F-measure、G-mean性能值提高地较小,CPU运行时间相差较小。
(2)对于不平衡率较高的人工数据集、Spectf Heart和Ecoli数据集,SVM分类器较易忽略少数类,因而分类性能较差。ALSMOTE-SVM和WSVM算法针对不平衡数据集适用性良好,但是较本文算法差,因为本文算法通过样本密度将多数类进行划分排序,保证每次参与分类器训练的多数类与少数类个数平衡,而且充分考虑类边界的样本信息。
(3)对于 Spectf Heart数据集,本文算法较其他算法的 G-mean提高了 5.59%,F-measure提高了6.43%,CPU运行时间降低了13%,表明本文改进策略使分类器的精度有较大的提高。
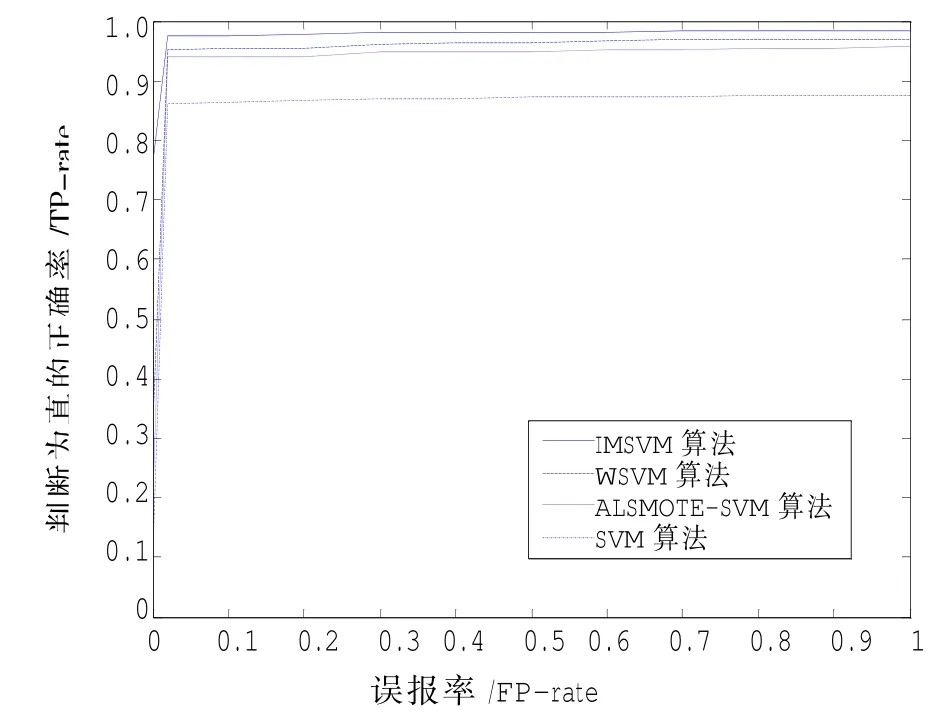
图3 4种算法在Dataset人工数据集上运行对应的AUC曲线Fig.3 The AUC curves of the four algorithms on the artificial dataset

图4 4种算法在Glass Identification数据集上运行对应的AUC曲线Fig.4 The AUC curves of the four algorithms on the Glass Identification dataset

图5 4种算法在Spectf Heart数据集上运行对应的AUC曲线Fig.5 The AUC curves of the four algorithms on the Spectf Heart dataset
AUC值,即ROC曲线与横轴围成区域的面积值,AUC大小可以反应分类器的性能。曲线越接近(0,1)点,且与横轴围成面积越大,分类器效果越好。由图3-5可以看出:
(1)对于均匀性较差的人工数据集Dataset,IMSVM算法得到AUC值为0.968,与SVM模型获得AUC值0.77要高出很多。
(2)对于不平衡性较轻的Glass Identification数据集,SVM算法的AUC值为0.877,其余3种改进SVM算法的AUC值都较高,说明改进SVM算法分类器性能良好,但IMSVM算法性能更好,从而证明在距离临界区域内的样本密度值划分多数类与相同数目的少数类完成SVM分类器训练的可行性。
(3)对于不平衡性较重的Spectf Heart数据集,SVM算法的AUC值为0.80,其余3种改进SVM算法的AUC值相差较大,IMSVM算法得到AUC值为0.971,说明用基于密度划分多数类,将边界区域的样本定义为对分类器“作用最大”,将靠近边界的样本定义为对分类结果“作用较大”的策略对于不均匀平衡数据集的分类效果良好。
(4)当4条不同曲线不相互交错的时候,位于上方ROC曲线对应分类器的性能优于位于下方分类器的性能,从曲线分布可知对于每个数据集,IMSVM建立的分类器性能优于其他算法模型分类器的性能,验证IMSVM算法的可行性。
3.3 对算法结果的影响
的选择决定样本局部密度的大小,如果取得太大或太小,都会降低 的区分度,严重影响分类精度。为证明 的大小对实验结果的影响,本文采用不同大小的 在不同的数据集Dataset、Glass Identification和Spectf Heart上实验,结果如图6-8所示。

图6 在人工数据集Dataset上,F-measure随 变化曲线Fig.6 F-measure variation curve with dcon the artificial dataset

图7 在Glass Identification数据集上,F-measure随变化曲线Fig.7 F-measure variation curve with dcon the Glass Identification dataset
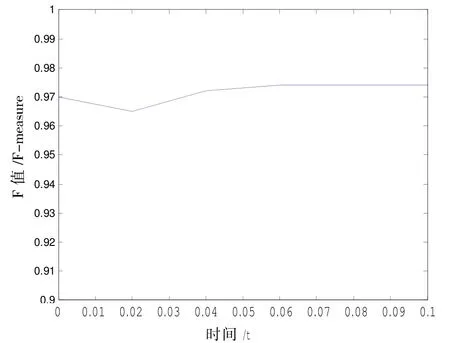
图8 在Spectf Heart数据集上,F-measure随 变化曲线Fig.8 F-measure variation curve with on the Spectf Heart dataset
从图6-8可知:不同数据集下 对分类结果的影响不一样。人工数据集Dataset和Spectf Heart数据集都有最优的 ,人工数据集Dataset比Spectf Heart数据集不均匀性高,因此所得F-measure曲线变化幅度更大些。Glass Identification数据集不均匀性较轻,分类结果F-measure为0.985,基本不受 的影响。所以针对不同的问题应选择合适的 参数。
4 小结
(1)本文针对传统分类方法对不均匀分布、边界信息模糊的不平衡数据集识别性能较低,提出基于新改进的SVM算法,即IMSVM。该算法先计算每个样本在距离临界区域内的密度值,再根据密度值的大小分别选出多数类边界区域、靠近边界区域的样本,且所选样本数目与少数类数目相同,保证训练样本的平衡性。将选取样本分别与少数类样本完成SVM初始分类,最后用所得的支持向量机和剩余的多数类样本对初始分类器迭代优化。
(2)实验结果表明IMSVM对不平衡数据集分类性能良好,证明了该算法的可行性和有效性。如何更好地协调相关参数的取值和降低时间复杂度是今后需要进一步研究的目标。

