基于融合函数构建的GPS车辆轨迹地图匹配算法

陈 滨

(闽江学院 现代教育技术中心，福建 福州 350108)

地图匹配算法是以GPS、北斗导航卫星等定位系统获得的轨迹数据及高精度路网信息作为输入，以此来识别车辆正在行驶的正确路段并确定车辆在路段上的位置[1].地图匹配算法主要有几何匹配算法、拓扑匹配算法、概率匹配算法、高级匹配算法[2]等，这些算法各有优缺点和使用范围，而如果要满足实际的路网需求，就必须寻求新的匹配算法.

1 匹配因素分析

影响地图匹配效果的因素很多，主要有：GPS定位点与候选道路之间的距离、航向差以及路网拓扑结构等，其中航向差因素是最重要的一个影响因子[3].

1.1 距离因素

GPS定位点到候选道路的距离是地图匹配的基本依据，也是最简单的一种匹配方式.其基本原理是由定位点向附近候选道路作垂线，定位点到垂足之间的距离d越小，匹配的可能性就越大[4].假设定位点为A(xa,ya)，垂足为B(xb,yb)，由两点间距离公式知

(1)

特殊情况下，由P点向候选道路作垂线，垂足不在道路上，而在道路的延长线上,这时就要比较P点与道路两个端点的距离，距离较小的端点即为匹配点.

则距离因子D可以由公式(2)量化，

(2)

由于实验所用导航仪的精度为10 m，根据概率分布的三倍标准差原则，所以这里的阈值则分别选取10 m和30 m.

1.2 航向差因素

航向差指车辆行驶方向与候选道路方向间的角度差值[5].为简明阐述航向差因素对地图匹配的影响，将以正北方向为方向角起点，以顺时针方向为旋转正方向，车辆当前航向和正北方向的夹角定义为车辆方向角α；同理，候选道路方向与正北方向的夹角定义为道路方向角β.则航向差θ定义为

θ=min(|α-β|,|α-β+π|)，

(3)

则航向差因子W可以由公式(4)量化，

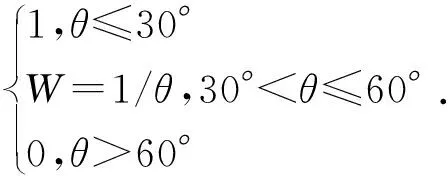
(4)

根据车辆行驶的实际情况，当航向角在30°以内时，车辆行驶方向与道路走向基本一致；当航向角大于60°时，车辆是偏离道路行驶的，匹配的可能性几乎为0.

1.3 路网拓扑结构因素

全局匹配算法的准确率一般会高于实时匹配算法，原因是全局匹配算法考虑了路网的拓扑结构T.在道路交通网络中，路网拓扑结构指候选道路与历史轨迹之间的连通性情况[6].

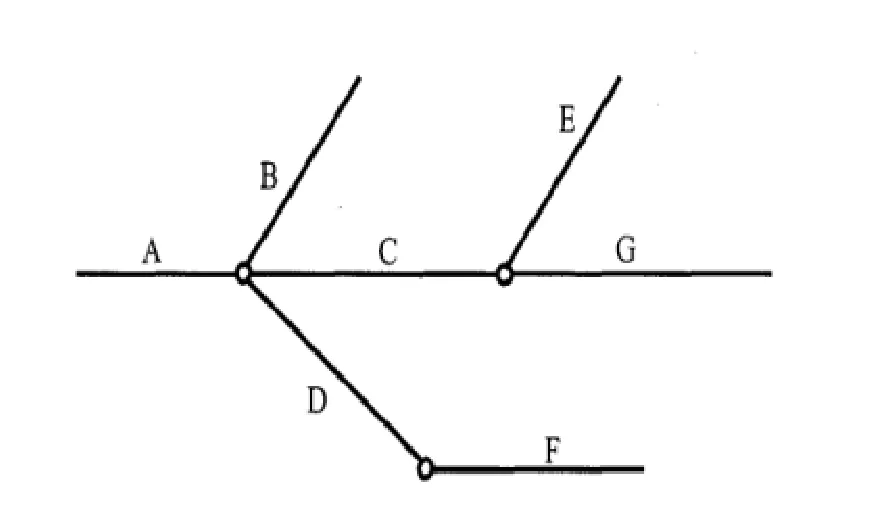
图1 路网拓扑结构示意图

如图1，假设前一时刻车辆行驶在A道路上，根据GPS采样点时间间隔以及车辆正常行驶速度推算可知，下一时刻车辆只可能行驶在B、C或者D道路上，而不可能跑到E、F和G道路上.因此，我们在下一时刻道路匹配时，候选道路只能在B、C和D中选择，就能减小候选道路的数量，提高匹配效率.如果候选道路与前一时刻轨迹相连通，T取1，否则取0.

基于拓扑结构的匹配算法，最大优点是在匹配之前，先利用路网的拓扑关系，筛选出可能的匹配道路，提高匹配效率.但是，该算法在使用过程中有一个前提条件，就是用来进行匹配的电子地图的精确度一定要足够高[7].

2 融合函数构建

从分析可知，距离、航向差以及路网拓扑结构因素都可以和接收的GPS定位点进行地图匹配，但这些匹配方法只能应用于一些特殊路段.随着道路交通网络的不断完善，在实际车辆行驶过程中，可能会遇到不同情况的路网结构，而依据单一的影响因子来判断匹配点往往具有片面性和局限性.因此，本文构建了以距离因子D、航向差因子W、道路拓扑因子T为变量的融合函数F(D,W，T)，融合函数具体表达式为

F(D，θ，T)=AP/D+AHW+ATT，

(5)

其中，AP(>0)是距离参数，投影距离D越小，权重越大，实验表明AP取任何一个正数都可以得到很好的结果；AH为航向角参数，根据实验取25有较好的匹配效果；AT为拓扑结构参数，当路网结构复杂时取1，否则取0.

2.1 定义域的确定

实验采取定义误差椭圆的方式确定融合函数的定义域，以降低计算复杂度.误差椭圆由公式(6)(7)(8)计算.

(6)

(7)

(8)

其中，Φ是误差椭圆的长半轴和Y轴正方向的夹角，a和b分别是椭圆的长半轴和短半轴，σx是GPS定位数据正东方向误差的标准差，σy是GPS定位数据沿着Y轴正方向误差的标准差，σxy和σ0分别是协方差和单位权值的方差.

2.2 融合函数流程图

为展现基于融合函数构建的地图匹配算法的工作原理，融合函数流程图如图2.首先将接收到的GPS数据进行预处理，以缩小数据处理量.然后核对GPS定位点是否在候选道路上，如果在就直接匹配；不在则分别依据距离因素、航向差因素以及拓扑结构因素判断候选道路；如果都无法确定，则依据融合函数来确定候选道路并匹配定位点.

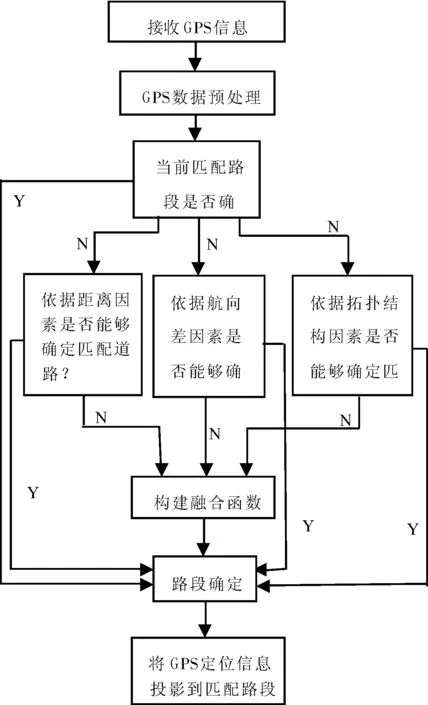
图2 融合函数匹配流程图

3 实验验证

为了对融合函数算法进行验证，本文进行实验仿真.实验过程中，采用南京市出租车GPS定位数据为实验数据，以matlab软件为仿真工具，同时结合Google Earth来显示电子地图.实验中，我们首先把某段时间内接收到的带有误差的GPS数据导入到Google Earth中绘制成原始的行车路线图，如图3所示，其中黑色线条为道路交通网络，黑色圆点为该段时间内接收到的车辆定位信息.车辆是自西向东行驶，经过一个路口后继续向西，然后在第二个十路路口右拐.可以看出，原始定位信息是有一定偏差，尤其在交叉路口会出现信号漂移的现象.

下面我们运用地图匹配算法对这些定位信息进行修正.首先，我们对原始数据进行预处理，剔除漂移点等不良信息.然后，运用融合函数匹配算法将剩余的GPS信号和电子地图网络之间进行匹配.最后，将匹配后的数据重新导入到Google Earth中，显示出匹配后的路线效果，如图4所示.可以看出，该算法能很好地去除信号漂移点，并且在十字路口、平行路段以及拐弯路段都有较好的匹配效果.

4 结语

地图匹配算法较好解决了车辆导航系统定位的不确定性问题，有助于修正导航系统的定位误差.融合函数的匹配算法实时有效，综合考虑了距离、航向差及道路拓扑结构等因素，得到了最优的位置估计信息，对于交叉路口的匹配具有较高的匹配精确度.

图3 原始轨迹图

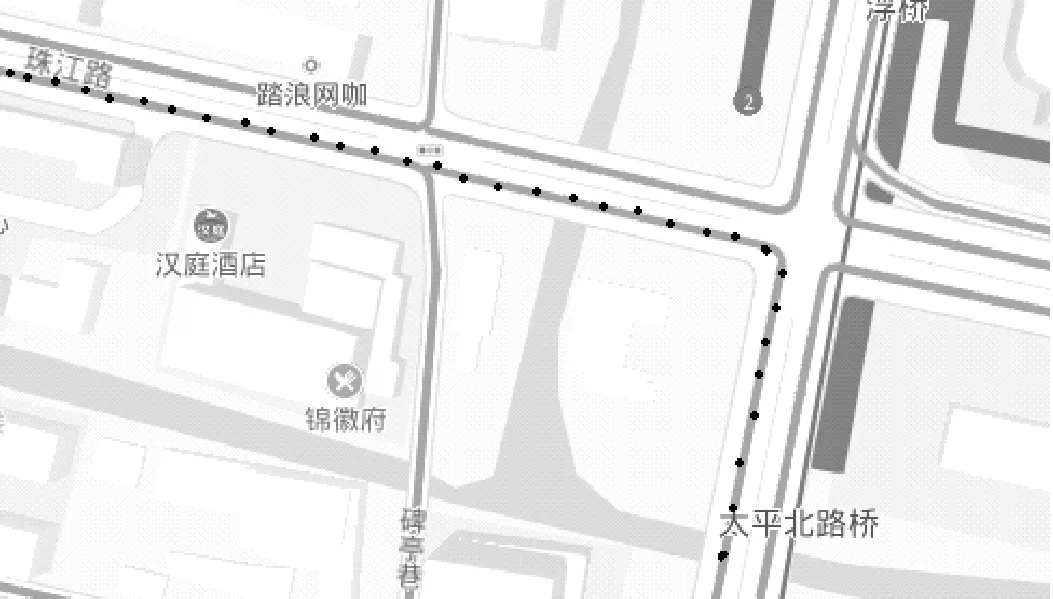
图4 融合函数匹配算法