与三角形面积有关的最值问题的求解策略

文/代润达

解三角形相关知识点是高考考查的重要内容，也是高考命题的热点部分，而且这部分内容往往易于和其他知识相结合，特别是三角函数、平面几何、解析几何、平面向量相结合，尤其是解三角形中的与面积有关最值问题和范围问题，结合正弦定理、余弦定理，常常利用三角函数的有界限性、基本不等式、函数求值域来求得最值，在高考各种题型中均有出现，如选择题、填空题、解答题，其试题难度属于中高档题，下面通过具体实例加以说明。

一、与三角函数相结合求最值

解三角形的面积问题，常常给出一些边和角的量，这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系，从而达到解决问题的目的.其基本步骤是：第一步：定条件，即确定三角形中的已知和所求，在图形中标出来，然后确定转化的方向；第二步：定工具，即根据条件和所求合理选择转化的工具，实施边角之间的互化；第三步：求结果，解题的关键是利用三角函数的有界性进而得解。

典例1.如图，在ΔABC中，角A, B, C的对边分别为a,b,c, a=b(sinC+cosC).

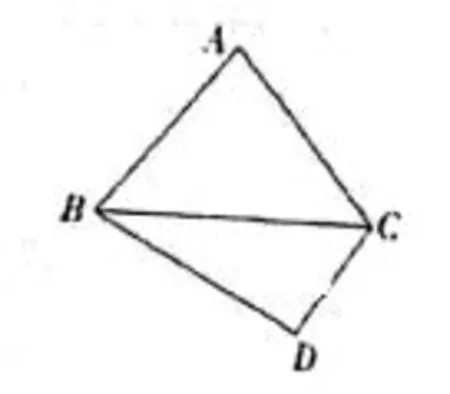
(1)求角B的大小；

试题分析：(1)先根据正弦定理将条件转化为角的关系sinA=sinB(sinC+cosC),再利用三角形内角关系、诱导公式及两角和正弦公式化简得cosBsinC=sinBsinC,即得，由余弦定理得，将数据代入可得利用配角公式得，最后根据三角形有界性可得四边形ABCD的面积最大值。

【评注】在解三角形中求最值范围问题往往需要转化为角的问题，利用辅助角公式，结合角的范围，利用三角函数的有界性求得最后结果。在边角互化中，注意化简和诱导公式的运用。

典例2. 源:学科在ΔABC中，三边a,b,c所对应的角分别是A, B, C，已知a,b,c成等比数列.

(2)若ΔABC外接圆的面积为4π，求ΔABC面积的取值范围.

(2)∵ΔABC外接圆的面积为4π，∴ΔABC的外接圆的半径R=2，

由余弦定理b2=a2c22accosB，得，又b2=ac，

由正弦定理，得b=4sinB.

【方法点睛】本题主要考查正弦定理及余弦定理的应用以及三角形面积公式.在解与三角形有关的问题时，正弦定理、余弦定理是两个主要依据. 除了直接利用两定理求边和角以外，恒等变形过程中，当条件中同时出现ab及b2、a2时，往往用余弦定理，而题设中如果边和正弦、余弦函数交叉出现时，往往运用正弦定理将边化为正弦函数再结合和、差、倍角的正余弦公式进行解答.

二、与基本不等式相结合求最值

有关解斜三角形面积问题，除了上面例题中利用正弦定理和余弦定理进行边化角，将求范围或最值问题，利用三角函数式恒等变形转化为某个角的三角函数式，根据角的范围研究函数值的范围，还有另一种方法是角化边，利用基本不等式求范围或最值。

典例3.在ΔABC中，已知a,b,c分别是角A, B, C的对边，且a=2。

试题分析：(1)由题意结合正弦定理可得ΔABC是等腰直角三角形，则；

(2)结合余弦定理得到面积的表达式，然后利用均值不等式的结论可得ΔABC的面积的最大值是1.

所以ΔABC的面积的最大值为。

【评注】：第一步利用正弦定理进行“边转角”化为三角函数关系，借助两角和公式进行恒等变形，求出角的余弦值，进而求出角；第二步利用余弦定理，转化为E与E的关系，然后利用基本不等式“等转不等”，求出E的范围，进而求出面积的范围。

三、利用二次函数求最值

在三角形的边角关系中，如果将三角形的面积转化为含有一个变量的函数关系，可借助函数求值域的方法求最值。

(2)记ΔABD与ΔBCD的面积分别是S1与S2，求的最大值

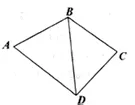
试题分析：)在ΔABD,ΔBCD中,分别用余弦定理,列出等式，得出的值；(2)分别求出S1,S2的表达式，利用)的结果，得到是关于C的二次函数,利用三角形两边之和大于第三边,两边之差小于第三边,求出BD的范围,由BD的范围求出C的范围,再求出的最大值。

解法二：

【评注】有关解斜三角形问题，常用正弦定理、余弦定理、面积公式等，多用正弦定理和余弦定理进行“边角转化”，求范围或最值问题常用方法有两种，第一边化角，利用三角函数式恒等变形转化为某个角的三角函数式，根据角的范围研究函数值的范围，另一种方法是化边，利用基本不等式或函数求值域方法求范围或最值。