基于层次分析法的危险品运输路径选择模型研究

李祖勤 田树新 曲庆龙 李书鹏

（91829部队 大连 116041）

1 引言

近年来，危险品的运输需求日益增多，在货物运输中的比重超过50%，其中80%左右通过道路运输完成［1～2］。通过科学的规划运输路线，能有效地选择事故风险低、成本小的路线进行运输，以减少道路危险货物运输的风险和可能产生的事故后果，并确保及时、畅通、高效地提供运输任务。

影响危险品运输的风险因素众多，其中既有定性指标也有定量指标，并具有系统化、层次化的特征，具有典型的多属性目标决策的特点。层次分析法（AHP）是一种决策使用方法，它是对多个方案、多个指标系统进行分析的一种结构化方法，通过使用数学方法来描述哲学的思维过程，以建立决策过程的数学模型，具有简单、有效的优点［3］。

文章利用层次分析法构造模型，充分考虑影危险品运输的各个因数，选择最优的运输路径，具有较强的现实意义。

2 AHP的基本步骤

应用AHP法解决问题的基本思路是：首先，把要解决的问题层次化，即根据问题的性质和需要达到的目标，将问题分解为不同的组成因素，然后按照因素之间的相互影响和隶属关系将其分成聚类组合，形成一个递阶的、有序的层次结构模型；其次，对模型中每一层各因素的相对重要性，依据人们对客观现实的判断给予定量表示，再利用数学方法确定每一层全部因素相对重要性的权重值，得到最低层（备选方案层）相对于最高层（总目标）的相对重要性排序的权重值，并以此作为评价和选择方案的依据［4］。

用层次分析法分析决策问题，大体要经过以下四个步骤［5～6］：建立层次结构模型；构造判断矩阵；层次单排序与一致性检验；层次总排序与一致性校验。

2.1 建立层次结构模型

经过调查研究找出与探讨问题牵连的主要因素，将这些因素按目标、准则、子准则、方案等分类，然后分层排列，构造一个反映各因素关联隶属关系的递阶层次结构模型，如图1所示。其中，最高层往往只有一个元素，表示分析问题的预定目标，称为目标层。最低层的元素往往是不同的决策方案，称为方案层（或要素层）。中间层次一般是准则层（或子系统），再下面是子准则层（或项目）。

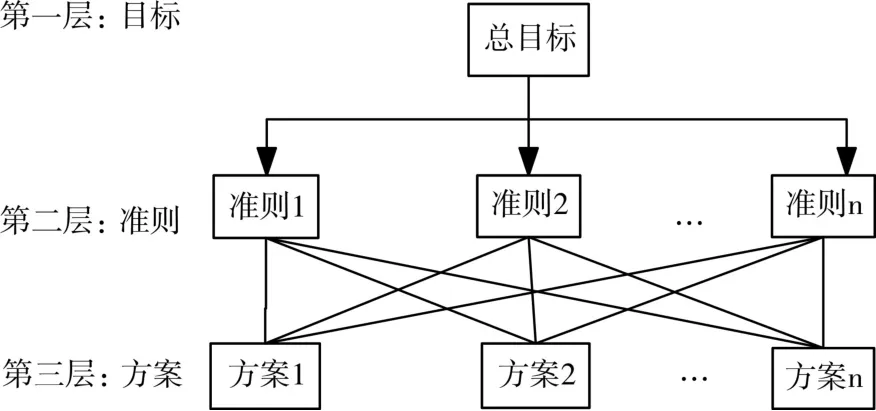
图1 层次结构模型

2.2 构造判断矩阵

在明确上层和下层元素间的隶属关系，进而建立起递进的层次结构，然后明确在单一准则支配下的上层元素后，下一层次元素权重的计算方法如下：

假设以顶层元素A为准则，其支配的下一阶层元素为 B1，B2，…，Bn。则判断矩阵为

式中，aij为元素Bi与Bj相对于A的重要性的1-9标度量化值，由表1量化得出。

表1 1-9标度量化值

2.3 层次单排序

层次单排序是指每一个判断矩阵各因素针对其准则的相对权重，其本质是计算权向量，方法通常有特征根法、和积法、方根法和幂法等，其中方根法算法步骤如下：

1）计算判断矩阵中各行元素的乘积Mi

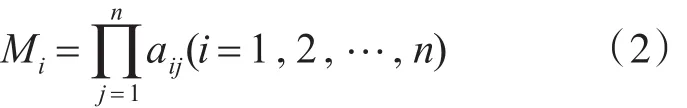
2）计算 Mi的 n次方根ωi

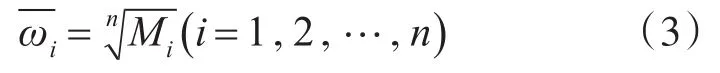
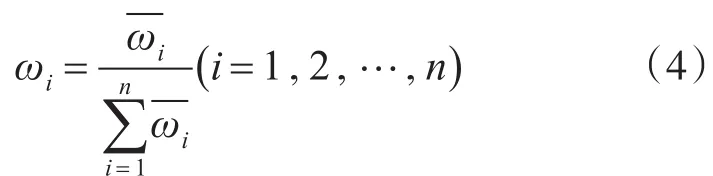
2.4 一致性检验

一致性检验是对判断矩阵的逻辑性进行检验，避免出现逻辑错误的一个过程，具体步骤如下：

1）一致性指标的计算。

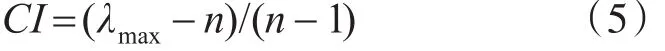
其中λmax为判断矩阵的最大特征根，计算方法如［7］式（6）

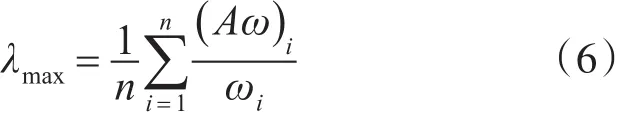
(A ω)i表示Aω的第i个分量。

2）平均随机一致性指标RI的获得，可通过表2查找得到。

表2 平均随机一致性指标

3）一致性比例CR的计算。

当CR＜0.1时，即要求专家判断的一致性与其他非专业人员随机判断的一致性之比小于10%时，认为一致性判断是可以接受的，反之，当CR≥0.1时，应当对判断矩阵适当修正，以保持一定程度的一致性［8］。

2.5 层次总排序

确定某层所有因素对于总目标相对重要性的排序权值过程，称为层次总排序。这一过程是从最高层到最底层依次进行的［9］。对于最高层而言，其层次单排序的结果也就是总排序的结果。

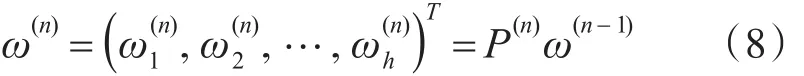
3 算例分析

3.1 建立层次结构模型

明确危险品运输路线的优化目标是确定运输路线的前提。道路运输危险品的特性决定了运输过程的特殊性，根据危险品运输对于安全的特殊需求，在运输路径的选择上，运输距离最短不是最重要的原则，而安全因素更为重要［10］。目标层确定后，准则层借助各方面专家的知识和经验来完成，本文采用德尔菲专家调查表法建立危险品运输路径选择层次结构模型，如图2所示。

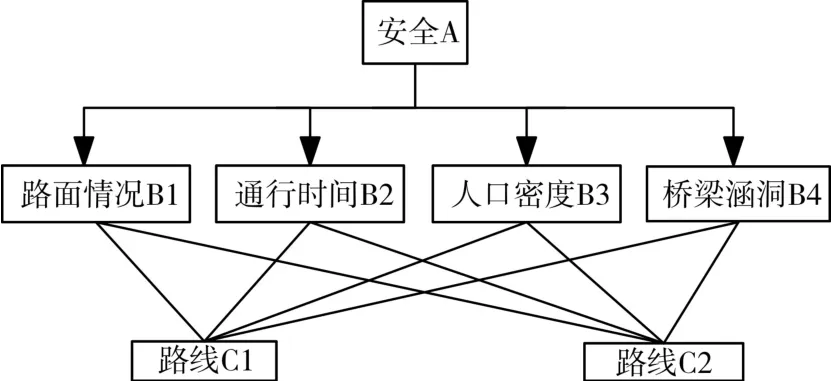
图2 危险品运输路径选择层次结构模型

其中路面情况B1是考虑包括道路是否平坦、宽阔，是否是水泥路等信息；通行时间B2既反映路途远近，也在一定程度上反映运输难易程度；人口密度B3考虑将群众生活不便降到最低；桥梁涵洞B4是指协调警力，避免不法分子蓄意破坏等因素。路线C1的情况：道路宽阔双向4车道，最近几年新铺设柏油路面，路途约25km，有大学2所，坐落较分散，沿途有上下坡，坡势比较平缓，有轻轨高架桥1座，汽车行驶约60分钟；路线C2的情况：道路较窄双向2车道，水泥路面，经常维护，路途约10km，有中学1所，路途平坦，汽车行驶约40分钟。

3.2 构造判断矩阵

邀请专家依据1-9标度量化法，可得判断矩阵A，B1，B2，B3和B4如下：

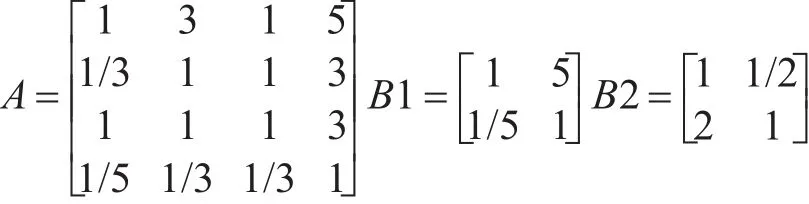
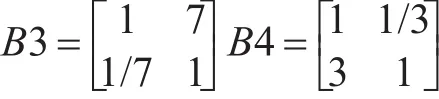
3.3 层次单排序

由式（2）、（3）和（4）可得各矩阵的特征向量为

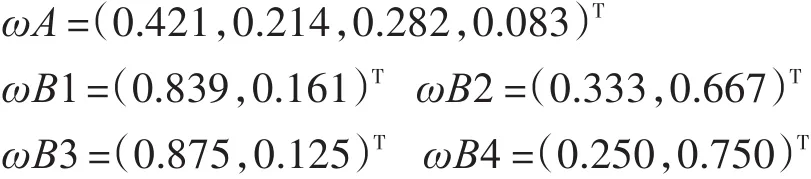
3.4 一致性检验

由式（6）可得 λmaxA1=4.11，λmaxB1=2，λmaxB2=2，λmaxB3=2，λmaxB4=2。

由式（5）可得 CIA1=0.037，CIB1=0，CIB2=0，CIB3=0，CIB4=0。

由式（7）可得 CRA1=0.043＜0.1，CRB1=CRB2=CRB3=CRB4=0，所有判断矩阵均通过了一致性检验。

3.5 层次总排序

由式（8）可得

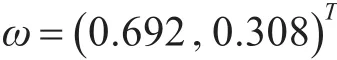
由此可见，路线C1的安全性远大于路线C2，与实际工作经验一致，说明文章建立的路径选择模型较好地反映了客观现实，为危险品运输的路径选择提供了决策依据。

4 结语

危险品运输过程中的路径选择是确保危险品安全的重要环节，文章采用层次分析的方法建立了评估模型，仿真结果表明，该方法简单、模型结构合理。