沥青路面表面纹理的多重分形特征及其磨光行为

周兴林 肖神清 刘万康 黄晓明 肖旺新

(1武汉科技大学汽车与交通工程学院, 武汉 430070)(2东南大学交通学院, 南京 210096)(3淮阴工学院交通工程学院, 淮安 223003)

沥青路面表面纹理对抗滑性能有着极其重要的影响.在交通荷载磨光作用下,表面纹理逐渐被磨光,路面抗滑性能逐渐下降,进而影响道路行车安全.沥青路面表面纹理磨光包括普遍磨光(general)和差异磨光(differential polishing)[1],集料软硬程度的不同导致产生这2种磨光现象.软硬程度不同的集料掺配有望成为抗滑表层选材技术的新方向[2].在磨光试验方面,研究主要集中于室内加速磨光模拟.首先,对磨光机(如德国Wehner-Schulze磨光机、亚琛磨光机等[3])施加特定荷载、速度及时间等磨光条件,将试件进行加速磨光;然后,分析不同磨光阶段试件表面的摩擦系数或纹理系数的变化,以揭示磨光行为.

表面纹理系数是路面抗滑性能的间接量化表征.通过激光扫描[4]或机器视觉[5]等方法重构出表面一维、二维乃至三维形貌,引入量化表面粗糙程度的参数[6-7],如表面几何参数、断面深度、分形维数以及功率谱等.然而,现有的表面纹理系数大多仅从整体考虑路面表面纹理的粗糙程度(如表面纹理的分形维数),只能反映整体的粗糙程度,缺乏对局部纹理的精细描述,故无法很好地反映出表面纹理的磨光行为.前期对多重分形理论的研究,将其从一维表面轮廓[8]向二维集料颗粒分布[9]有益转化,发现相对于简单分形,多重分形能够表达表面纹理更加丰富的信息.基于此,本文将多重分形表征方法由二维向三维表面形貌进一步深入,验证沥青路面表面纹理的多重分形特性,以谱参数来量化交通载荷下沥青路面表面纹理的变化,从而更加全面地反映出交通荷载作用下的沥青路面磨光行为,为探索路面磨光机理奠定基础.

1 表面三维形貌的多重分形特征参数计算

分形几何学广泛应用于图形图像的分析处理,并已经较多地运用到道路工程领域中.多重分形是分形的一种延伸,具有多重分形特性的对象可分为多个区域的复杂分形结构.采用投影覆盖法(PCM)[10],以不规则平面面积作为研究物理量.如图1 所示,用边长为εL的正方形网格(ε为尺度,且0<ε≤1)来覆盖边长L的图像,通过网格4个顶点对应的高程进行计算,得到第i行j列的网格对应的不规则平面面积Sij(ε),计算公式为

(1)

(a) 盒覆盖法 (b) 覆盖盒子对应的投影面

由式(1)可知,投影面高差越大,则平面越陡,Sij(ε)也越大.随着尺度ε越小,投影面积越来越大,表面越来越复杂.通过双对数下Sij(ε)与ε的拟合直线的斜率,可由下式求得分形维数D[11]:

lnSij(ε)=(2-D)lnε+C

(2)

式中,C为常数;2-D表示拟合直线的斜率.

构建不同尺度下网格的概率测度Pij(ε)为

(3)

式中,∑Sij(ε)为尺度ε下所有网格对应面积之和.对于多重分形的对象,概率测度Pij(ε)可用奇异性标度指数αij来表征,二者满足如下关系式:

Pij(ε)∝εαij

(4)

式中,αij为奇异性标度指数,反映了第i行j列网格面积的奇异程度.根据盒维数法的定义,可以统计出相同奇异性标度指数α的网格(概率子集)数目Nα(ε).将具有相同α的概率子集的分形维数定义为f(α),则

Nα(ε)∝ε-f(α)

(5)

式(4)和(5)表明,多重分形谱中大奇异指数αmax及对应的分形维数f(αmax)反映的是小概率测度平坦区域的性质;反之,小奇异指数αmin及对应的分形维数f(αmin)则反映的是大概率测度陡峭区域的性质.多重分形谱宽Δα和两侧高差Δf分别为

Δα=αmax-αmin

(6)

Δf=f(αmin)-f(αmax)

(7)

由式(6)可知,Δα反映了整个分形结构上概率测度分布不均匀程度,Δα值越大,整体上表面概率测度分布越不均匀,相对陡峭的差距越大,表面也就越粗糙不平.由式(7)可知,高差Δf用来统计最大概率子集数目与最小概率子集数目的相对数量,当Δf>0时,主要反映了表面陡峭区域的占优程度,反之则反映的是表面平坦区域占优程度.

对概率测度Pij(ε)的q次方进行加权求和,构成配分函数族χq(ε),即

χq(ε)=∑Pq(ε)

(8)

式中,q为概率测度的阶数.式(8)可作为验证研究对象是否具有多重分形特性的依据[12].在实际计算中,常采用文献[13]中的方法进行计算,即

(9)

式中,u(q,ε)为正交化的函数族.则多重分形谱的计算公式为

(10)

将α(q)和f(q)分别作为自变量和因变量对应在α-f(α)坐标上,即可得到多重分形谱图像.对应的谱宽Δα和高差Δf可通过式(6)和(7)求得.

2 表面纹理磨光试验

2.1 材料特性

试验材料选取秦皇岛产地的石灰岩集料与70#基质沥青,沥青的基本性能参数见表1,粗集料部分物理力学指标见表2.参照规范[14-15],各项指标参数均符合规范要求.试件采用AC-13典型级配类型(见表3),油石比为4.8%.级配关键性筛孔通过率大于40%,属于细型密级配.主要体积参数通过马歇尔试验(试件直径为101.6 mm,双面各击实75次)获取,分别采用塑封真空法和表干法测得混合料理论密度和毛体积密度,进一步计算得到混合料的空隙率为4.66%.

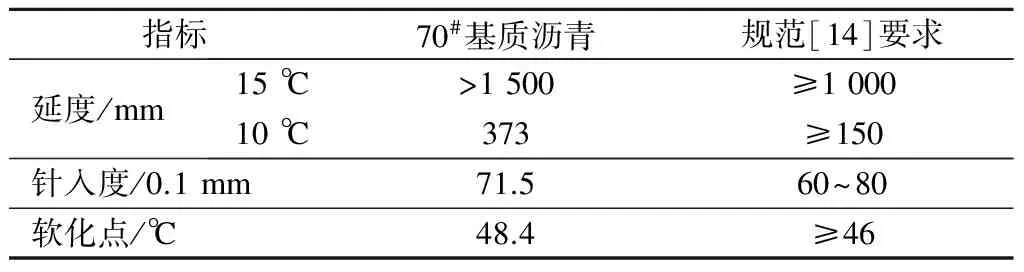
表1 秦皇岛70#基质沥青性能

表2 粗集料物理力学性质

表3 沥青混合料级配

2.2 磨光试验

按照规范[14]成型尺寸为300 mm×300 mm×50 mm的车辙板试件,然后采用内径为250 mm的钻芯机得到圆柱形试件,将试件洗净、常温晾干.采用自主研发的平板磨光机(见图2(a),其原理类似于Wehner-Schulze磨光机),3个锥形磨光头橡胶轮呈120°分布,圆心位置为砂-水混合物喷嘴(见图2(b)).六边形柱体的镂空结构(见图2(c))可按试件大小细微调节,沥青混合料圆柱形试件直径约为250 mm,磨光环形带内径约为100 mm,外径约为225 mm.进行磨光前,通过计算机控制伺服电机使磨光头下降至接触试件表面,然后设置相应的磨光参数:磨光荷载设为标准轴载100 kN,转速设为500转/min(汽车低速行驶速度约为20 km/h),磨光转数w=0,2×104,4×104,6×104,8×104,1×105.

(a) 平板磨光机

(b) 磨光部件

(c) 试件放置

图2沥青混合料磨光试验

2.3 数据采集

对同一块磨光试件选取4个区域进行定点观察.当磨光转数到达预设值后,采用手持的三维激光扫描仪FreeScan X3(见图3,Z向测量精度达0.03 mm)对磨光表面进行扫描,利用Digimetric软件将获取的数据点经GREC Pro模块自动拼接,实现表面形貌三维重构.为重点分析磨光区域不同磨光阶段的表面纹理变化情况,采用反光标志点(内径6 mm,外径10 mm)进行标识,方便MATLAB软件对三维数据进行二次提取.

(a) 手持三维激光扫描仪

(b) 三维形貌获取

3 磨光结果分析与讨论

3.1 表面纹理的多重分形特性

为验证沥青路面表面纹理的多重分形特性,以磨光前w=0时4 cm×4 cm方形测量区域为例(见图4),设定高程最低点所在水平面为基准面,其高程设为0.根据式(8),利用MATLAB软件编写多重分形程序,计算得到q在-100～100间尺度ε与配分函数χq(ε)的关系,结果见图5.由图可知,不同阶数q下,散点近似构成一条直线,说明三维形貌具有分形标度特征.各阶q下直线斜率明显不同,说明三维形貌还具有多标度特征.因此,表面

图4 沥青路面三维表面纹理

图5 配分函数χq(ε)与尺度ε的关系

三维形貌具有多重分形特性.实际上,沥青路面表面纹理一维轮廓、二维颗粒分布具有的多重分形特性是三维形貌的低维表现,这里所述的三维,通过数字矩阵形式表示,并不是严格的三维空间,而是一种准三维空间.

3.2 结果分析

3.2.1 磨光表面的构造深度变化

为比较直观地反映表面纹理各磨光阶段的高程变化,将获取的数字相对高程以云图形式表示.图6(a)～(f)反映了测点1在不同磨光阶段的相对高程情况,将各云图中表面最低点高程设为0,各图例中高程范围相同.由图6可知,随磨光转数的增加,表面纹理构造深度逐渐减小,表面渐趋于平坦.

3.2.2 磨光表面的分形参数变化

为量化每个磨光阶段表面纹理的变化,图7给出了4个测点在不同磨光转数下的表面纹理多重分形谱.由图可知,各测点的多重分形谱均呈右钩状,形状较为相似,说明随着表面高程的减小,表面纹理保留了整体的形状特征.各磨光状态下的谱宽明显发生变化,但高差基本变化不大.投影覆盖计算方法采用的是二维平面覆盖,得到的多重分形谱峰值为2,这是一个期望的结果[13].多重分形谱右侧主要反映的是小概率测度(极平坦区域)的变化情况,当q<0时,小概率测度比大概率测度变化明显,当q逐渐减小趋于负无穷时,右侧值出现聚集,此时q的变化已对多重分形谱影响不大;同理,多重分形谱左侧则反映了大概率测度(极陡峭区域)的变化情况.

图8绘出了各磨光阶段测点的分形维数D、谱宽Δα、高差Δf等分形特征参数变化情况.由图8(a)可知,磨光前各测点的分形维数比较接近(约为2.250),而后随磨光作用分形维数均逐渐减小,在w=1×105时分形维数约为2.175,变化率为3.3%左右,变化较小,说明单从分形维数的角度来分析表面纹理磨光行为是不够的.为此,进一步分析了分形特征参数的变化情况.如图8(b)～(c)所示,各测点的谱宽Δα和高差Δf变化存在差异,测点2的谱宽和高差衰减趋势最为明显,测点1和4谱宽变化明显,但其高差变化较小.

(a) w=0

(b) w=2×104

(c) w=4×104

(d) w=6×104

(e) w=8×104

(f) w=1×105

(a) 测点1

(b) 测点2

(c) 测点3

(d) 测点4

(a) D的变化

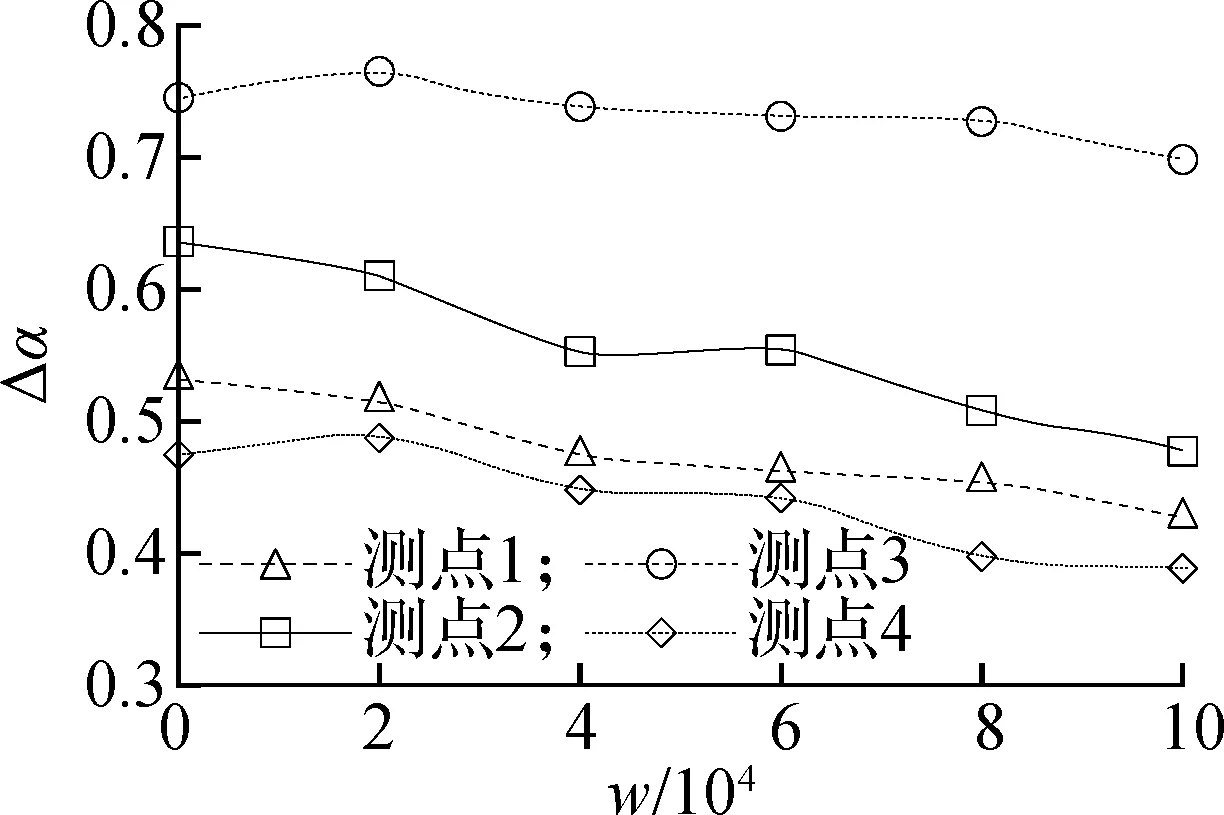
(b) Δα的变化

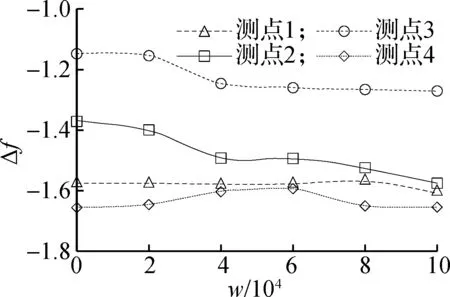
(c) Δf的变化

谱宽Δα反映了概率测度分布的不均匀程度,是区别于构造深度的表征参数,与高程值并无直接联系.Δα越小,说明大概率和小概率测度越相近,即表面纹理表现多为光滑的平坦区域;反之,Δα越大,表面则表现为尖锐突出的粗糙区域,即表面相对粗糙.沥青路面形貌随磨光作用总是趋于磨平的结果,陡峭区域逐渐被削弱,整体趋于平坦,故Δα出现了明显的下降趋势.另一方面,各测点间的磨光衰减程度并不一致,测点3和4在磨光过程中谱宽Δα略有上升,说明磨光后的局部区域相对表现得更陡峭尖锐,这种越磨越糙的表面纹理变化结果也符合差异磨光的磨光机理.

高差Δf反映了大概率测度(极陡峭区域)与小概率测度(极平坦区域)的数目相对情况,其值越小,说明小概率测度越占优,表面也就相对平坦、光滑.理想情况下的二维平面,并无陡峭与平坦区域之分,高差Δf的理论值为0,表示陡峭区域与平坦区域数目相等.但在图8(c)中,各测点的高差Δf衰减情况并不一致,也没有趋于0的变化趋势,而是总体表现为小幅度波动并逐渐趋于稳定.这可以解释为,分布在集料表面的沥青薄膜是不均匀的,加上集料形状的无规则性以及磨光作用的差异性等因素,表面粗糙在磨损过程中又会产生新的粗糙,如混合料内部的闭口空隙成为表面的开口空隙,从而无法形成理想状态下的二维平面,表面总是以平坦区域占优.

4 结论

1) 基于多重分形理论验证了沥青路面表面纹理具有多重分形特性,其多重分形谱能较全面反映表面纹理特性.多重分形谱宽Δα反映的是表面相对粗糙的整体特征,高差Δf则量化了陡峭区域(或平坦区域)占优的局部特征.

2) 多重分形谱参数能进一步量化表面纹理的磨光行为.随着荷载磨光作用,表面构造深度减小,路面纹理逐渐被磨平,分形维数D变化较小,无法很好地描述磨光作用的差异性,而谱宽Δα随磨光作用呈现较为明显的衰减规律,同时表面平坦区域占优程度渐趋于稳定.

3) 多重分形作为量化磨光行为的一种新方法,后续可以进一步验证其实用性.例如通过不同软硬程度的集料掺配,研究表面纹理磨光的多重分形特征参数变化规律,侧重分析越磨越糙的表面纹理变化,从而给出普遍磨光与差异磨光的定量解释,结合工程抗滑性能指标,得到满足路面性能要求的优选组合.

)

[1] Tourenq C, Fourmaintraux D. Road surface roughness and the properties of aggregates[J].BulletindeLiaisondesLaboratoiresdesPontsetchaussées, 1971,51: 61-69.

[2] 李菁若,张东长,谭巍.粗集料的抗滑耐磨性能评价新方法[J].公路交通科技,2016,33(12):76-82. DOI:10.3969/j.issn.1002-0268.2016.12.012.

Li Jingruo, Zhang Dongchang, Tan Wei. A novel method for evaluating skid-resistance and wear-resistance performance of aggregates[J].JournalofHighwayandTransportationResearchandDevelopment, 2016,33(12): 76-82. DOI:10.3969/j.issn.1002-0268.2016.12.012.(in Chinese)

[3] Chen X, Dai S, Guo Y, et al. Polishing of asphalt pavements: From macro-to micro-scale[J].JournalofTestingandEvaluation, 2015,44(2): 20150271. DOI:10.1520/jte20150271.

[4] Cui X, Zhou X, Lou J, et al. Measurement method of asphalt pavement mean texture depth based on multi-line laser and binocular vision[J].InternationalJournalofPavementEngineering, 2015,18(5): 459-471. DOI:10.1080/10298436.2015.1095898.

[5] El Gendy A, Shalaby A, Saleh M, et al. Stereo-vision applications to reconstruct the 3D texture of pavement surface[J].InternationalJournalofPavementEngineering, 2011,12(3): 263-273. DOI:10.1080/10298436.2010.546858.

[6] Kogbara R B, Masad E A, Kassem E, et al. A state-of-the-art review of parameters influencing measurement and modeling of skid resistance of asphalt pavements[J].Construction&BuildingMaterials, 2016,114: 602-617. DOI.org/10.1016/j.conbuildmat.2016.04.002.

[7] Chen X H, Wang D W. Fractal and spectral analysis of aggregate surface profile in polishing process[J].Wear, 2011,271(11): 2746-2750. DOI:10.1016/j.wear.2011.05.024.

[8] 周兴林,肖神清,肖旺新,等.粗集料表面纹理粗糙度的多重分形评价[J].华中科技大学学报(自然科学版),2017,42(2):29-33. DOI:10.13245/j.hust.170206.

Zhou Xinglin, Xiao Shenqing, Xiao Wangxin, et al. Multi-fractal evaluation on roughness of coarse aggregate surface texture[J].JournalofHuazhongUniversityofScienceandTechnology(NaturalScienceEdition), 2017,42(2): 29-33. DOI:10.13245/j.hust.170206.(in Chinese)

[9] 周兴林,肖神清,冉茂平.基于多重分形理论的沥青路面集料离析评价方法[J].武汉科技大学学报(自然科学版),2016,39(4):284-288. DOI:10.3969/j.issn.1674-3644.2016.04.009.

Zhou Xinglin, Xiao Shenqing, Ran Maoping. Evaluation of aggregate segregation of asphalt pavement based on multifractal spectrum[J].JournalofWuhanUniversityofScienceandTechnology(NaturalScienceEdition), 2016,39(4): 284-288. DOI:10.3969/j.issn.1674-3644.2016.04.009.(in Chinese)

[10] Miao Y, Song P, Gong X. Fractal and multifractal characteristics of 3D asphalt pavement macrotexture[J].JournalofMaterialsinCivilEngineering, 2014,26(8): 04014033. DOI:10.1061/(asce)mt.1943-5533.0000912.

[12] 王维锋,严新平,肖旺新,等.路面纹理的多重分形特征描述与识别方法[J].交通运输工程学报,2013,13(3):15-21.

Wang Weifeng, Yan Xinping, Xiao Wangxin, et al. Approach of multifractal feature description and recognition for pavement texture[J].JournalofTraffic&TransportationEngineering, 2013,13(3): 15-21. (in Chinese)

[13] Chhabra A B, Meneveau C, Jensen R V, et al. Direct determination of thef(α) singularity spectrum and its application to fully developed turbulence[J].PhysicalReviewAGeneralPhysics, 1989,40(9): 5284-5294. DOI:10.1103/physreva.40.5284.

[14] 交通运输部公路科学研究院.JTG E20—2011公路工程沥青及沥青混合料试验规程[S].北京:人民交通出版社,2011.

[15] 交通运输部公路科学研究院.JTG F40—2004公路沥青路面施工技术规范[S]. 北京:人民交通出版社, 2004.