一种新的非奇异积分型Terminal滑模控制

廖怡娜，金朝永

（广东工业大学应用数学学院，广东广州510520）

研究非线性不确定系统时，滑模变结构控制是一种非常实用的工具,在通常情况下，滑模面函数的选取一般都是线性的，这个线性切换函数能够确保系统在有限时间内到达滑模面，并且进入滑模阶段后系统会渐进稳定到平衡点或者跟踪误差收敛到零，但是不能保证收敛到平衡点的时间有限。为了获得更好的控制性能，Venkataraman［1］提出了Terminal滑模控制策略，即在滑模面的设计上引入非线性函数，这样不但可使系统在有限时间内到达滑模面，而且可以在有限时间内稳定到平衡点。有限机理Terminal滑模就是在这种背景下发展起来的。但是文献［2］指出，Terminal滑模控制中容易产生奇异问题，目前有两类方法来解决控制结构中出现的奇异问题，第1类是间接法［3］，即将原来Terminal滑模分为两部分，并且部分增加为线性或非线性的形式；第2类是直接法［4］，即采用其他非线性函数来替换原来Terminal滑模函数的非线性部分，以确保控制器的非奇异性。

滑模变结构控制对系统内部的参数和外部干扰具有很好的鲁棒性，为解决系统内部参数摄动和外界干扰引起的稳态误差和增强鲁棒性，Chern［5］在传统的滑模面设计上引入误差积分项来削弱稳态误差和提高鲁棒性，后来，将这种积分滑模运用在永磁同步电机设计控制中，但在比较大的初始误差值下，较大的超调及积分饱和效应就会出现了，甚至会造成系统的不稳定［6］。为了防止发生饱和效应，李鹏等［7］通过改进积分滑模面函数，在边界层外用调节因子来衰减积分项，以避免初始误差较大的情况下饱和效应的产生引起的超调较大，在边界层内的稳态误差采用传统积分来减少。之后，李鹏等［8］提出一类具有“小误差扩大，大误差饱和”无穷可导的非线性饱和函数来完善传统的积分滑模控制。

本文在文献［7-11］的基础上改进全局快速Terminal滑模控制的滑模面，避免了变结构控制奇异问题的产生，另一方面，各误差项用各状态量代替，所设计变结构控制器只需被跟踪信号已知即可，并不需要连续信号的可导条件。

1 问题提出

首先，研究一类二阶不确定非线性系统

其中，x=［x1，x2］T为系统的状态变量；f（x）和b（x）≠0且为x的光滑非线性函数；g（x）为不确定性干扰且满足为控制输入。

考虑全局快速Terminal滑模（GFTSM）的切换函数

其中，α，β为正实数，p 和 q 为正奇数，且 p＞q。

当系统状态到达滑模面（2）上时，状态x1（t）≠0收敛到平衡点的时间为

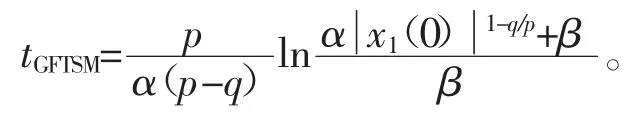
控制器设计为

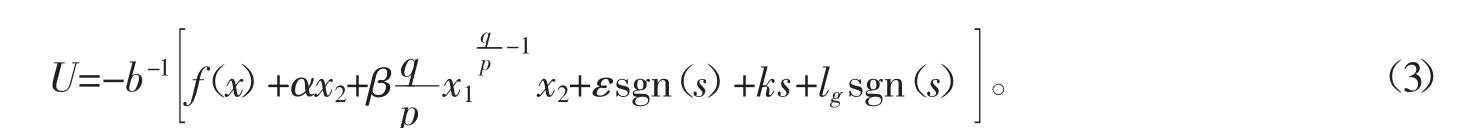
从滑模面（2）可以看出，在远离平衡点时系统收敛到滑模面的速度由决定，在趋近于平衡点时系统收敛到滑模面的速度由αx1决定，在线性滑模面上引入吸引子虽然加快了滑模控制的收敛速度，但是引入的吸引子却容易产生奇异问题。分析如下：对于Terminal滑模（2）所设计的控制器（3）中含有 x1q/p-1x2项，因为 p，q 为正奇数，且 p＞q，所以 q/p-1＜0，在 x1=0，x2≠0 时会产生奇异问题。当 s=0 时，即在理想的滑模面上，有 x2=-αx1-βx1q/p，x1q/p-1x2=-αx1q/p-βx12q/p-1，如果规定 1＜p/q＜2，就可避免奇异问题发生。但当s≠0时，即在到达终端滑模面的阶段，当x1=0时，x2=s≠0。在上述控制律U下，系统（1）到达Terminal滑模面之前，并不能保证x1=0和x2≠0的状态不出现，否则，便会有奇异问题产生，此外，由于计算误差等不确定因素，在到达Terminal滑模面之后也可能产生奇异问题，尤其是在x1=0，x2=0平衡点附近，会不定时地产生奇异问题。若考虑奇异问题，采用间接法或直接法所得到的状态在滑动模态上的收敛时间就会增长，为了避免奇异问题，缩短系统到达滑模面上的时间，本文将设计一种新的滑模切换函数。

2 Terminal滑动模态控制的设计

在滑模变结构控制中，控制分两步进行：一是保证滑模阶段的存在，系统状态稳定收敛到滑模面s=0上；二是使得系统在滑模面上收敛到期望动态或者误差零点［12］。

为了克服GFTSM存在的奇异问题［13］，本文提出一种新的Terminal滑模控制器，设计一个新的如下Terminal滑模函数（简称GFITSM）

其中，α＞0，β＞0，p 和 q 为正奇数，且 p＞q。

s沿解的时间导数为

取指数趋近律，即

则

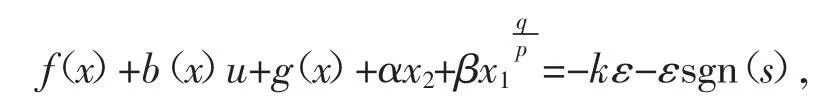
化简后，设计新的控制律为

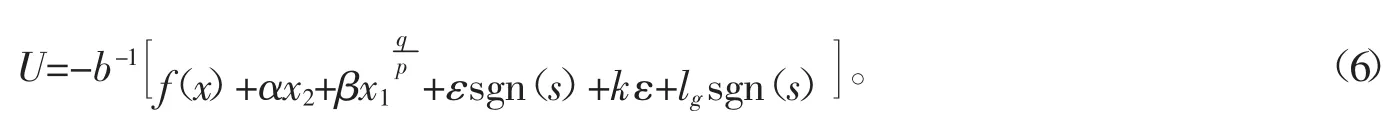
定理1 对非线性系统（1），取滑模面函数（4），在控制律（6）的作用下，则系统状态能够在有限时间内渐进稳定到达滑模面s=0上。

证明 系统稳定性分析：选取Lyapunov函数，即

对Lyapunov函数求导，则

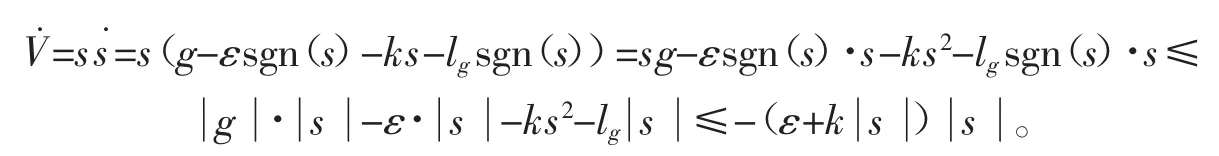
由于 ε＞0，k＞0，于是V觶≤0，证明系统滑动模态的存在。

设s（0）≠0到s=0时间为tr，当t=tr时，s（tr）=0。

由

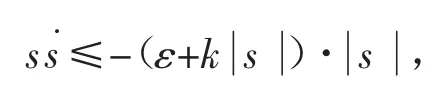
当 s≥0 时，有

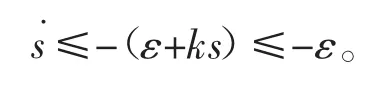
注1为了系统抖振能更好地削弱，一般采用sat（s）饱和函数来替代sgn（s）平滑控制量，即

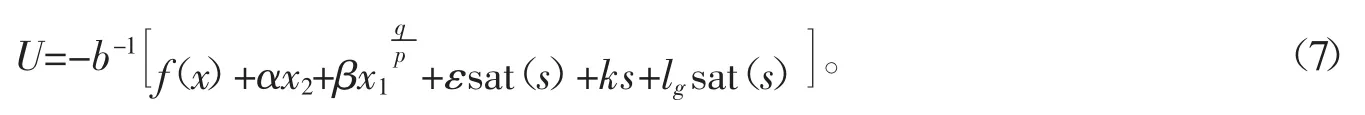
这里的sat（s）为饱和函数，定义为

其中，φ为很小的正数。替换后的控制量（7）使得滑动模态存在并依然可到达。

定理2 对于非线性系统式（1）和控制策略式（6），系统状态在滑模面式（4）上是全局渐进稳定到平衡原点。

证明 系统稳定性分析：当系统状态变量进入滑模面s=0，此时也有觶=0，即取Lyapunov函数，即

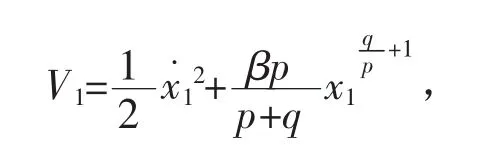
V1是正定的，而

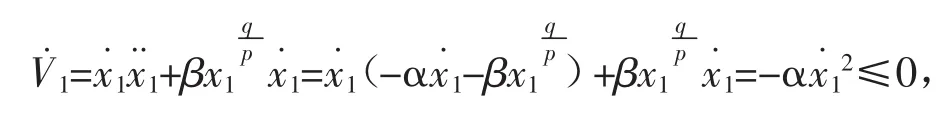
3 设计改进的滑动模态控制器

令y=x1，ym=xm为跟踪期望信号，定义跟踪误差为

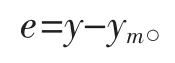
对于系统（1），为了减少稳态误差和提高系统的鲁棒性［14］，在传统的滑模面表达式上加入误差的积分项其滑模面设计如下［7］

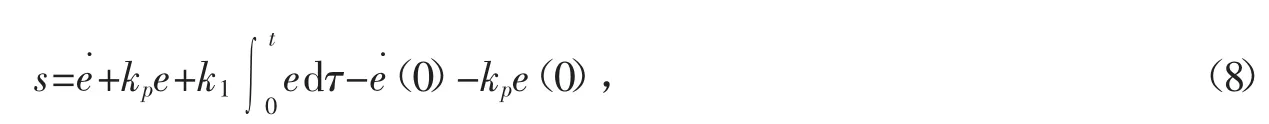
其中，kp＞0，k1＞0。对于滑模面（8），使得在初始状态系统就处于滑动模态上，消除了到达过程。然而在比较大的初始误差值下，较大的超调及积分饱和效应就会出现了，甚至会造成系统的不稳定。李鹏等［8］提出一类具有“小误差扩大，大误差饱和”无穷可导的非线性饱和函数来完善传统的积分滑模面控制。文献［11］各误差项用各状态量代替，所设计变结构控制器只需被跟踪信号已知即可，并不需要连续信号的可导条件。

因此，设计新的滑模面为

其中，α＞0，β＞0，p 和 q 为正奇数，且 p＞q。

定理3 对于非线性不确定系统式（1），取式（9）定义的滑模面，若控制律为

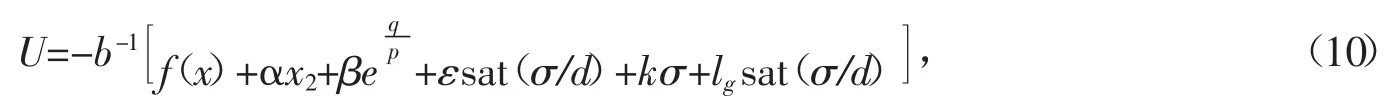
其中，d为边层厚度，则滑动模态变量σ能在有限时间内进入边界层。证明 当滑动模态变量σ不在边界层内时，式（10）可以写成

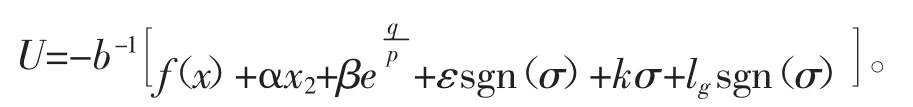
选取Lyapunov函数，即

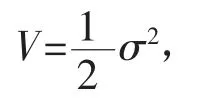
对Lyapunov函数求导，则

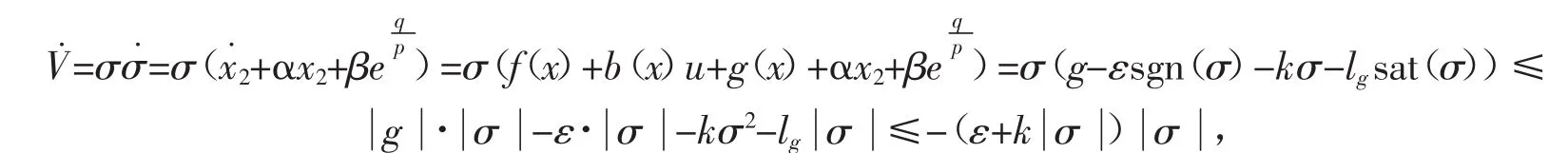
由于 ε＞0，k＞0，于是V觶≤0，说明系统滑动模态存在。

所以，σ能够在有限时间tr内到达边界层内，tr为

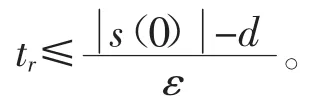
注2在控制器U的表达式中可以看出，只需要期望输出值ym，并不需要各阶的导数。边层法可以让系统状态收敛到以滑模面为中心的边层内。

定理4 对于系统（1）和控制策略式（10），假设输入的期望信号具有一阶可导且β满足

则系统在滑模面上的跟踪误差e收敛趋近于0。证明 取Lyapunov函数，即

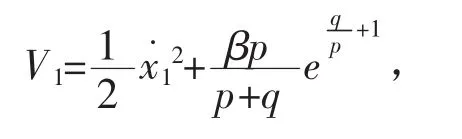
V1是正定的，而

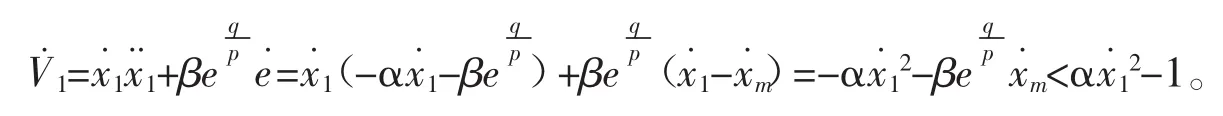
4 仿真结果及分析

为了验证本文提出的全局快速非奇异积分型Terminal滑模控制方法的有效性，这里的simulink仿真将与全局快速Terminal滑模控制（2）进行比较。

考虑一个简单的二阶非线性不确定动态系统

其中，f=0.1sin（20t），g=0.12sint；参数选择为 p=5，q=3，α=1，控制律中的参数 lg=0.015，ε=0.20，k=5。

选取全局快速Terminal滑动模态的控制方法，这种滑模对应的切换函数记为GFTSM，则滑模函数为

选取全局快速非奇异积分型Terminal滑模的控制方法，对应的切换函数为GFITSM，则滑模切换函数为

结合以上两种Terminal滑模的控制方法，所设计的控制器形式如下：

（1）GFTSM控制器为

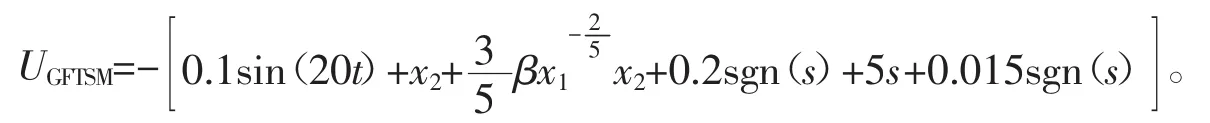
（2）GFITSM控制器为

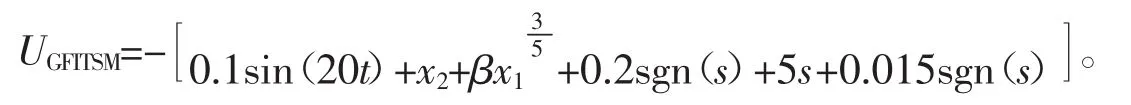
结论1本文提出的GFITSM控制器可以保证全局快速Terminal滑模在非奇异的前提下，实现系统的快速收敛。为了与全局快速终端滑模GFTSM控制器作比较，选取系统的初始状态为x1（0）=0.5，x2（0）=0，β=4，如图1~3所示，GFTSM控制器的状态变量x2和控制u都产生很大的抖振，而本文设计的控制器却能达到稳定状态，并且状态变量越趋近于平衡点（x1（0）=0，x2（0）=0），参数β选取越大，GFTSM的状态变量x2（t）及控制u抖振得越厉害。

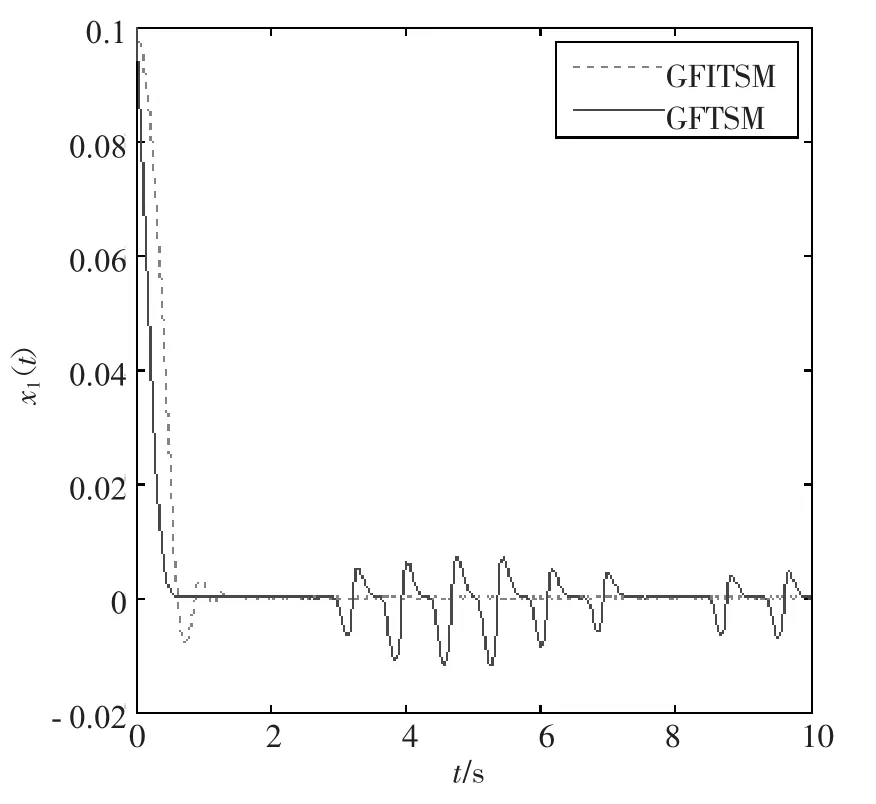
图1 2种滑模控制器下状态x1（t）的抖振研究曲线

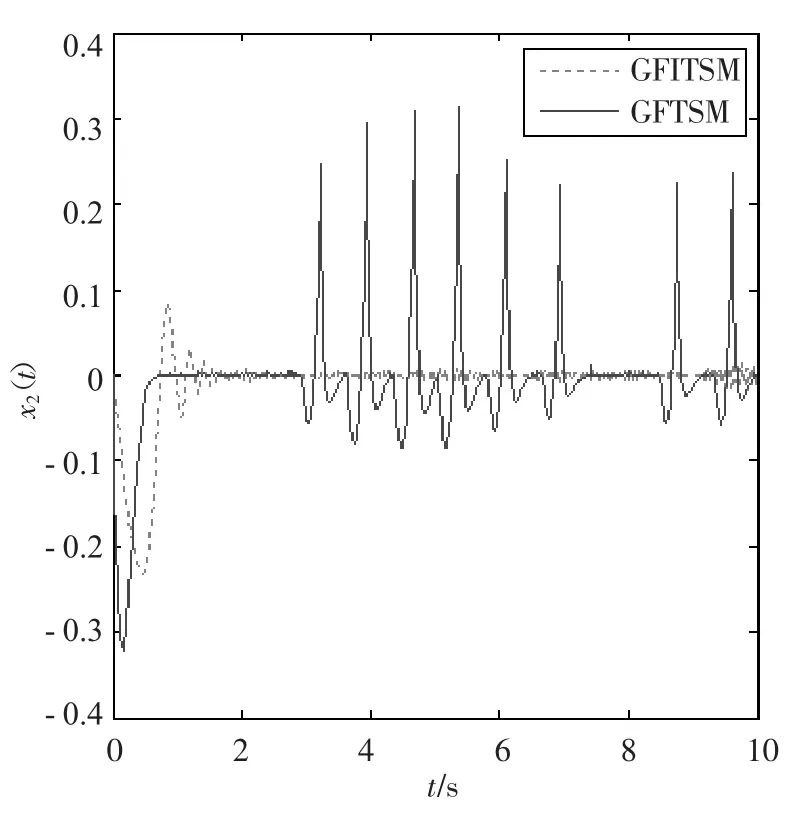
图2 2种滑模控制器下状态x2（t）的抖振研究曲线

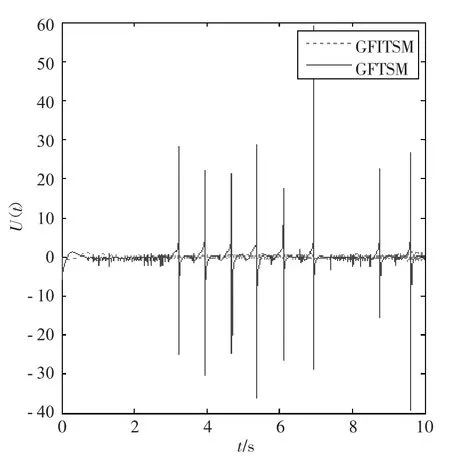
图3 2种滑模控制器下控制输入的抖振研究曲线

结论2观察图4~6的仿真结果，在两种控制器的作用下，两种滑模面都可以在有限时间内收敛到平衡点，而本文提出的全局快速非奇异积分型Terminal滑模控制比GFTSM具有更快的速度收敛到平衡点。这里初始状态x1（0）=1，x2（0）=5，参数其余参数保持不变，系统从初始值分别进入区域的收敛时间如表1所示，从表1可看出，与控制器GFTSM相比，本文提出的GFITSM控制器的状态变量x1（t）收敛速度快约20.2%，而状态变量x2（t）的收敛速度快约13.3%。因此，本文提出的新的控制器是最有效的。

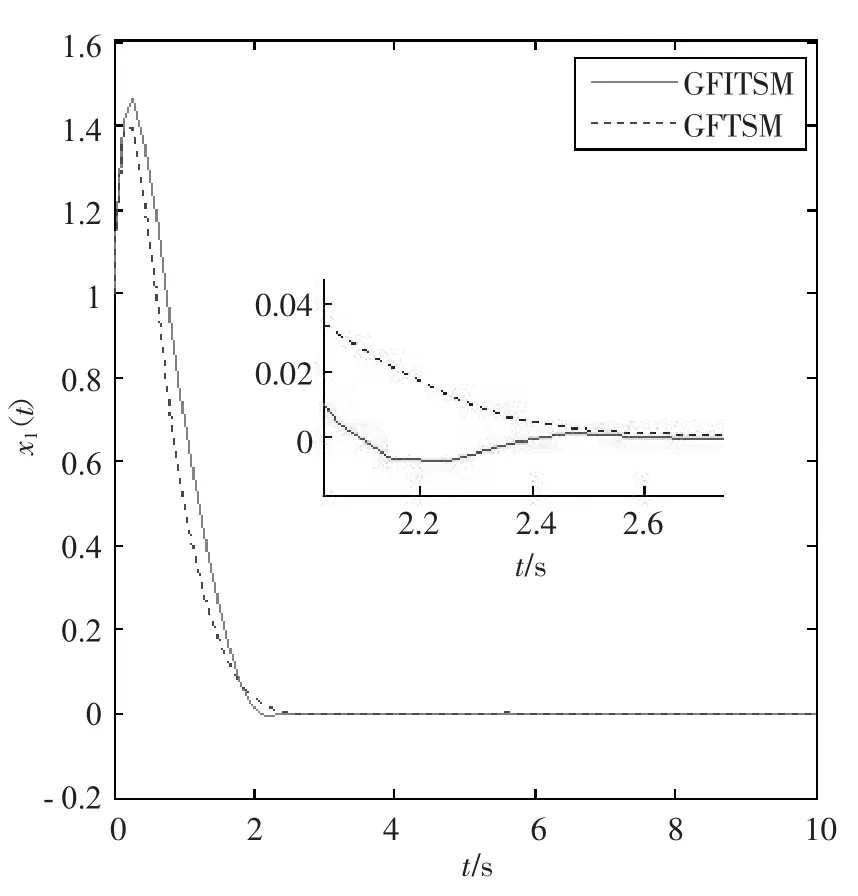
图4 2种滑模控制器下状态x1（t）的收敛速度曲线

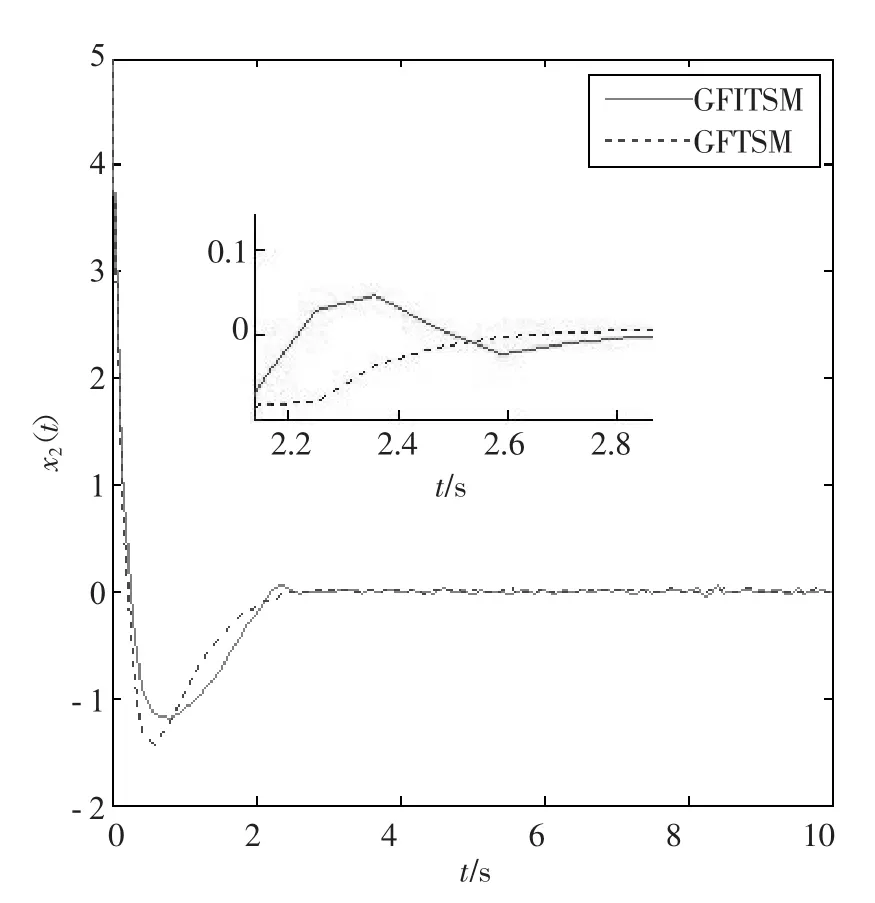
图5 2种滑模控制器下状态x2（t）的收敛速度曲线

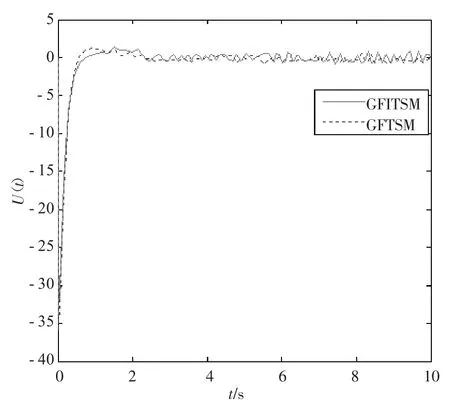
图6 2种滑模控制器下控制输入的收敛速度曲线

表1 2种滑模控制器下系统状态变量的收敛时间

5 结论

针对一类SISO二阶不确定非线性系统，本文设计了一种新的非奇异Terminal滑模控制，并和原有的全局快速Terminal滑模控制相比，可以避免奇异问题，削弱状态变量及控制器的抖振。根据Lyapunov稳定性定理，证明了系统在有限时间达到滑模面且在有限时间收敛到平衡点。仿真结果表明［15］，本文提出的非奇异积分型Terminal滑模控制可以在更短的时间内收敛到平衡点。

［1］VENKATARAMAN S T,GULATI S.Terminal slidingmodes:a newapproach to nonlinear control systems［C］//Proceedings of the 5th IEEE International Conference on Robotics and Automation.WashingDC:IEEE,1991.

［2］KANG B P,LEE J J.Comments on“A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators”［J］.IEEE Trans on Automatic Control,1996,41（5）:716-762.

［3］ZOU A,KUMAR K D,HOU Z,et al.Finite-time attitude tracking control for spacecraft using terminal sliding mode and chebyshev neural network ［J］.IEEE Transactions on Systems,Man,and Cybernetics-Part B:Cybernetics,2011,41（4）:950-963.

［4］CHIU C.Dervative and integral terminal sliding node control for a class ofMIMO nonlinear systems［J］.Automatica,2012,48（2）:316-326.

［5］CHERN T L,WU Y C.Design of integral variable structure controller and application to electrohydraulic velocity servosystems［J］.IEEE Proceedings-D,1991,138（5）:439-444.

［6］SLOTINE J J.Application Nonlinear Control［M］.NewJersey:Prentice-Hall,1991.

［7］李鹏,马建军,李文强,等.一类不确定非线性系统的改进积分型滑模控制［J］.控制与决策,2009,24（10）：1463-1466.

［8］李鹏,郑志强.非线性积分滑模控制方法［J］.控制理论与应用,2011,28（3）:421-426.

［9］张巍巍,王京.基于指数趋近律的非奇异Terminal滑模控制［J］.控制与决策,2012,27（6）:909-913.

［10］郭建国,贾齐晨,周军.一种非线性系统积分Terminal滑模的控制系统设计［J］.河南师范大学学报,2015,43（6）:1-7.

［11］管成.非线性系统的滑模自适应控制及其在电液控制系统中的应用［D］.杭州:浙江大学,2005.

［12］FENG Y,YU X,MAN Z.Non-singular terminal sliding mode control of rigid manipulators［J］.Automatica,2002,38（12）:2159-2167.

［13］熊柯,夏智勋,郭振云.倾斜转弯高超声速飞行器滚动通道的自适应全局积分滑模控制［J］.国防科技大学学报,2012,34（2）：114-118.

［14］KHOO S,XIE L,MAN Z.Integral Terminal Sliding Mode Cooperative Control of Multi-robot Networks［C］//IEEE/ASME International conference on advanced intelligent mechatronics.Washington D C:IEEE Society,2009:969-973.

［15］刘金坤.滑模变结构控制MATLAB仿真［M］.2版.北京:清华大学出版社,2012:12-43.