HPM视角下的初等数论绪论课教学设计
杜先存+李玉龙+杨慧章
摘要:从HPM的视角研究了关于初等数论绪论课的课堂教学设计。首先从初等数论的课程价值及教学现状出发,介绍了初等数论的主要内容及学科发展简史。其次,简单介绍了几个重要数论难题,了解这些难题的研究状况。最后,通过数学名著及相关人物,介绍了我国古代数学的伟大成就及国外古代数学的成果,让数学史料融入初等数论的教学中,使学生能从整体上对初等数论有个初步认识。
关键词:HPM;数学史;初等数论;数学教学
一、 引言
初等数论以整除为基础,研究整数性质和方程(组)整数解,是近代数学中最典型、最基本的概念、思想、方法和技巧。初等数论课程是我校小学教育(理科方向)和数学教育专业的专业必修课,学生通过本课程中基础知识的学习,掌握初等数论的基础内容,即算术基本理论和最大公约数理论;掌握初等数论的核心,即同余理论的基本知识;并能运用整除理论和同余理论来求解几类最基本的不定方程;掌握连分数等有关概念和性质及其应用;通过观察、实验、猜测、分析、计算、推理等学习活动,发展学生的演绎推理能力,体会数学的基本思想和思维方式;了解初等数论的价值,为学生以后继续学习数论或从事教学工作打下基础。然而,初等数论教材重在阐述数论理论知识的结果,忽视介绍知识的背景、发生与形成过程,某种意义上影响了该课程的教学质量。
针对初等数论课程的性质,在绪论课中结合数学史知识,在HPM的视角下进行绪论课的教学设计,HPM视角下的绪论课教学的目的在于将初等数学与数学史等其他知识衔接起来,尽量消除数学教学的枯燥性,提高学生学习的积极性,让学生体验初等数论的价值,进而增强学生的使命感和目标感,吸引更多的学生热爱数学,变被动学习为主动学习。HPM指的是数学史与数学教育的关系,其研究的最终目标是提高数学教育水平,具体方法是通过在数学教学中恰当地运用数学史。
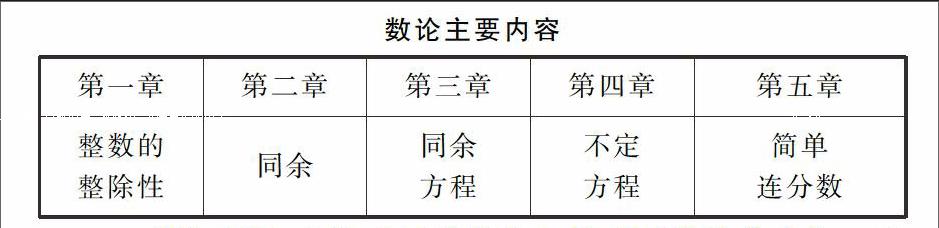
二、 初等数论的主要内容
1. 整除理论:整除理论是数论中最重要的基本内容。本章首先简要介绍自然数与数学归纳法,然后引进整除的概念,利用带余除法和辗转相除法这两个工具,建立最大公约数与最小公倍数的理论,进一步研究素数的基本性质和极具重要性的算术基本定理。这一理论的主要成果有:算术基本定理、数的十进制、高斯函数、费马数、梅森数、完全数等。
2. 同余理论:同余是初等数论的又一基本概念。同余概念的引入,使许多数论问题的讨论得到简化,极大地丰富了数论内容,因而同余在数论中占有极为重要的地位.涉及内容有同余及其基本性质,剩余类与剩余系,欧拉定理和费马定理及其在循环小数和公开密钥问题上的应用。
3. 不定方程:不定方程是数论中的一个古老分支,它有悠久的历史与丰富的内容.古希腊数学家丢番图于3世纪初就研究过这样的方程,所以不定方程又称丢番图方程.但实际上,我国对不定方程的研究从勾股方程的商高定理和费马大定理等低次代数曲线对应的不定方程已经延续了数千年。
4. 连分数理论:引入了连分数概念和算法等等。特别是研究了整数平方根的连分数展开。主要成果:循环连分数展开、最佳逼近问题等。
三、 初等数论的发展简史
对数的崇拜和好奇是促使人们去研究数的原始推动力,这样一门以整数的结构和性质为研究对象的学科也就诞生了,这就是数论。目前大多数人大致赞同数论的研究在内容上是从数的可约性开始的。若“可约”,则它是一个整除性问题;若“不可约”,则为余数问题。因此,整除理论被称为是数论中最古老的内容。早在两千多年前的古希腊欧几里德的《几何原本》中论述了数论的知识,例如欧几里得证明了质数个数是无限的,提出了求最大公约数的方法(即所谓欧几里得算法)。我国古代在数论方面取得过辉煌的成就,现在一般数论书中被称为“中国剩余定理”的孙子定理就起源于我国古代《孙子算经》(约公元400年)中的下卷第26题。
初等数论从早期发展起来后的近两千年时间里,发展几乎停滞不前,直到15世纪,费马、欧拉、拉格朗日、勒让德和高斯等作了初等数论的研究工作,特别是德国数学家高斯在前人研究的基础上,发表了著作《算术探究》,在研究整数性质过程中引进并推广了统一的符号,提出了同余理论,发现了二次互反律,开始了现代数论的新纪元。
自二十世纪以来,由于现代信息技术的发展以及抽象数学和高等分析的应用,进一步促进了数论的发展,并出现了代数数论、解析数论、几何数论等新的研究分支,开拓了应用范围,如在计算机科学、组合数学、代数编码、计算方法等领域内都得到了广泛的应用。
四、 几个著名的数论难题
历史上遗留下来没有解决的数论难题主要有:哥德巴赫猜想;费尔马大定理;孪生素数问题;完全数问题等。
1. 哥德巴赫猜想:1742年德国人哥德巴赫提出了任何不小于6的偶数均可表示为不同的两个奇质数之和(所谓的1+1)的猜想。后人称之为”哥德巴赫猜想”,此猜想表述简单,但证明的难度远远超出人们的想象,比喻为“数学王冠上的明珠”。1900年德国大数学家希尔伯特在国际数学会议上将“哥德巴赫猜想”列为第8个问题(23个数学难题)的一部分。1973年中國数学家陈景润用自己提出的方法证明了命题(1+2),即:一个足够大的偶数可以表示为一个素数和一个不超过两个素数的乘积之和,在世界数学界引起了强烈反响,这就是著名的“陈氏定理”。
2. 费尔马大定理:费马大定理又称费马最后的定理,由法国数学家费马于1637年前后提出,费马在阅读丢番图《算术》时在第Ⅱ卷第八命题旁写道:“一个立方不可能写成两个立方的和,一个四方不可能写成两个四方的和。一般地,每个大于2的幂不可能写成两个同次幂的和。”现在的表述方法为:“方程xn+yn=zn(n≥3)无非零整数解。”
该数论难题由英国数学家Andrew Wiles于1994年攻克。
3. 孪生素数猜想:存在无穷多个素数p,使得p+2也是素数。素数对(p,p+2)称为孪生素数。1849年法国数学Alphonse de Polignac 提出猜想:对于任何偶数2k,存在无穷多组以2k为间隔的素数。对于k=1,这就是孪生素数猜想,而k等于其他自然数时就称为弱孪生素数猜想。2013年5月,华人数学家张益唐在孪生素数研究方面所取得的突破性进展,他证明了孪生素数猜想的一个弱化形式。endprint
4. 完全数问题:完美数又称为完全数,最初是由毕达哥拉斯的信徒发现的,他们注意到,数6有一个特性,它等于它自己的因子(不包括它自身)的和,如:6=1+2+3。下一个具有同样性质的数是28,28=1+2+4+7+14。接着是496和8128。他们称这类数为完美数。
欧几里德在大约公元前350-300年间证明了:若2n-1是素数,则2n-1(2n-1)是完全数。目前已发现的完全数都是偶完全数,有没有奇完全数至今尚无定论。
五、 我国古代数学的伟大成就
1. 周髀算经:《周髀算经》成书不晚于公元前2世纪西汉,是中国古代完整地流传至今最早的一部天算著作。大约从东汉末期开始,人们已经把这部书当成是专门论述中国古代三大宇宙学说之一——盖天说的理论著作。主要成就为提出了著名勾股定理的一个特殊情况——“勾三股四弦五”,并将勾股定理应用于天文测量中。
2. 孙子算经:《孙子算经》原名《孙子算数》,作者名不详,成书年代约为公元400年。现在传本的《孙子算经》共上中下三卷。该书上卷是关于筹算法则的系统介绍,下卷则有著名的“物不知数”问题(西方数学史称其为”中国剩余定理”),亦称“孙子问题”,后发展为更一般的“大衍求一术”。
3. 算数书:《算数书》成书于公元前3世纪,是中国目前已发现的成书年代最早的算学著作,大约比现有传本的《九章算术》还要早近200多年。《算数书》在内容、体例等方面对《九章算术》的产生有直接的影响。《算数书》是一本数学问题集,共有69个题名,完整的算题92个,单独成题的6个。其主要成果为分数约分、加减乘除四则运算、比例等算术知识,也有面积公式、体积公式等几何知识。
4. 九章算术:中国古代数学专著《九章算术》成书于东汉时期,全书共方田、粟米、衰分、少广、商功、均输、盈不足、方程、勾股九章,涉及分数、面积体积、勾股定理等246个数学问题,问题后有相应解答。是中国古代数学体系形成的标志,自此,中国数学家,大多是以《九章算术》作为教材、范本开始学习和研究数学知识。《九章算术》以算筹为工具,以算法为主要内容,以应用问题集为形式,与古希腊数学完全不同的独立体系。标志着中国传统数学的知识体系已初步形成,其思想方法对我国古代数学产生了巨大的影响。
5. 海岛算经:中国数学家刘徽注解经典数学名著《九章算术》之后附了一份问题集,后整理成《海岛算经》,书中9题算例,涉及测高望远及其计算问题。
六、 外国古代数学的丰硕成果
1. 莱因德纸草书:《莱因德纸草书》成书年代约为公元前1650年,是古埃及数学典籍,属于世界上最古老的数学著作之一。纸草书主要讲述了古埃及的乘除法、单位分数的用法,求圆面积问题及一些数学的实际应用等。
2. 几何原本:古希腊数学家欧几里得所著《几何原本》成为古西方应用逻辑典范而影响深远。该书共分13卷。书中包含了5条“公理”、5条“公设”、23个定义和467个命题。第Ⅶ、Ⅷ、Ⅸ三卷是数论,分别有39、27、36个命题,也完全用几何的方式叙述,第Ⅶ卷第1命题是欧几里得辗转运算法的出处。第Ⅸ卷第20命题是数论中的欧几里得定理:素数的个数无穷多。
《几何原本》从5个“不证自明的”公理和点、线等少数几个原始定义出发,通过逻辑推理得出整个几何体系,成为人类历史上的科学杰作。
3. 算术:《算术》是古希腊数学家丢番图的一部代数著作,成书于公元3世纪。《算术》是一本问题集,书中主要涉及一次或多次方程和二次不定方程代数问题以及数论方面的问题及解题方法,代表了古希腊代数思想的最高成就。该书丢番图自称共有13卷,但现仅存6卷,共有189题,几乎一题一法,各不相同。并且,这部著作中引用了S、△r△、Kr等许多缩写符号。17世纪法国数学家韦达正是在丢番图缩写代数的启示下才做出了符号代数的贡献。
4. 代数学:阿拉伯数学家花拉子米著作《代数学》,书中给出了一元二次方程的一般解法及几何论证,引进了移项、合并同类项等代数运算,指出了二次方程无(实)根的条件等等。全书由三部分组成,分别讲述了初等代数、实用算术问题和有关遗产继承问题。全书不使用代数符号,而是用语言叙述。
5. 几何学:法国数学家笛卡尔1637年出版著作《更好地指导推理和寻求科学真理的方法论》,其中一个附录《几何学》共分三编,提出了方程和曲线的思想,《几何学》也成为了解析几何经典之作而被人们所接受。
6. 几何基础:德国数学家希尔伯特1899年出版著作《几何基础》,从此奠定了现代公理化方法。
参考文献:
[1]韩灵娟,阮佶主编.初等数论[M].长春:吉林大學出版社,2016.
[2]张楠,罗增儒.对数学史与数学教育的思考[J].数学教育学报,2006,15(3):72-75.
[3]汪晓勤,张晓明.HPM研究的内容与方法[J].数学教育学报,2006,15(1):16-18.
[4]王进明.初等数论[M].北京:人民教育出版社,2008.
[5]孙宏安.孪生素数猜想[J].中学数学教学参考,2004(6).
[6]姜靖.华人数学家张益唐:敲开世纪数学猜想大门[J].科技致富向导,2014(2).
[7]钱宝琮.算经十书·孙子算经提要[M].北京:中华书局,1963.
[8]盛文林.人类在数学上的发现[M].北京:北京工业大学出版社,2011(10).
[9]崔智超.《莱因德纸草书》研究[D].辽宁师范大学,2006(5).
作者简介:杜先存,李玉龙,云南省蒙自市,红河学院教师教育学院;
杨慧章,云南省蒙自市,红河学院数学学院。endprint

