高考中三视图还原几何体的对策研究
广东省雷州市第八中学(524232) 魏欣 邓春梅
在近几年的高考考察中,利用三视图求直观图体积或表面积的题型屡见不鲜,这种题型的本质即为由三视图还原直观图,所以要求学生掌握由三视图还原直观图的解题技巧显得尤其重要.画简单几何体的三视图对大部分学生来说并不困难,但是,由三视图还原出几何体,对学生的空间想象能力和综合分析能力提出了较高的要求,出现错误的机会明显增加.本文针对出现的问题“对症下药”,给出确定的三视图还原直观图的方法,让学生有迹可循,为学生空间观念的培养打好基础,进而培养学生的空间想象能力和逻辑思维能力.
一、熟悉基本概念
正视图是指光线从几何体的前面向后面正投影得到的投影图;侧视图是指光线从几何体的左面向右面正投影得到的投影图;俯视图是指光线从几何体的上面向下面正投影得到的投影图.其规律为:一个几何体的正视图和侧视图高度一样,正视图和俯视图长度一样,侧视图与俯视图宽度一样.简称:长对正,宽相等,高平齐.如下图所示,正四棱锥的三视图,从中我们可以看出,三视图还原原几何体的线段很清晰对应着.

二、熟悉基本的几何体的三视图特点
1.直棱柱的三视图特点:正视图与左视图是矩形(可以有若干条平行于矩形一条边实线或虚线),俯视图为多边形.如图1.2.

图1

图2
2.直棱锥的三视图特点:主(正)视图与左(侧视图)视图是三角形(可以有若干条从顶点到底边的实线或虚线),俯视图为多边形(可以有若干个共同顶点的三角形).如图3.4.
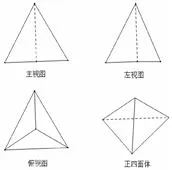
图3

图4
3.棱台的三视图特点:主(正)视图与左(侧视图)视图为若干个上下底共线的梯形排成的大梯形;俯视图为若干个梯形,其上下底分别围成多边形,形成网状.如图5.6.
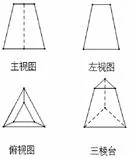
图5

图6
4.圆柱的三视图特点:主(正)视图与左(侧视图)视图为全等的矩形,俯视图为圆.如图7.

图7

图8
5.圆锥的三视图特点:主(正)视图与左(侧视图)视图为全等的三角形,俯视图为圆.如图8.
6.圆台的三视图特点:主(正)视图与左(侧视图)视图为全等的梯形,俯视图为两个同心圆.如图9.

图9

图10
7.球体的三视图特点:三个视图均为全等的圆.如图10.
8.斜棱柱的三视图特点:主(正)视图为平行四边形,左(侧视图)视图为矩形,俯视图为矩形(可以有若干条平行于矩形一条边实线或虚线).如图11.

图11
为了方便记忆,由以上八种熟悉的基本的几何体的三视图特点,可以总结出破解此类题型的“高考秘诀”为:
两视矩形,看柱体,另为圆,则圆柱;另为多边形,则棱柱.两视三角形,看锥体,另有曲,则圆锥;另全直,则棱锥.两视梯形,看台体,另为同心圆,则圆台;另网状,则棱台.三视为圆则为球.
三、三视图还原的基本方法
方法 1.定型式—先底面,再顶点
例1(2016年新课标全国III文科第10题)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )


解析 由斜棱柱的三视图特点,正视图为平行四边形,侧视图为矩形,俯视图为矩形,则还原图为斜四棱柱,上下底面为正方形,其面积:3×3×2;前后面为两个平行四边形,其面积:3×6×2;左右侧面为矩形,其面积:3×35×2.则该多面体的表面积为
3×3×2+3×6×2+3×35×2=54+185,所以选择B.
变式1(2016年四川文科第12题)已知某几何体的三视图如图所示,则该几何体的体积等于.

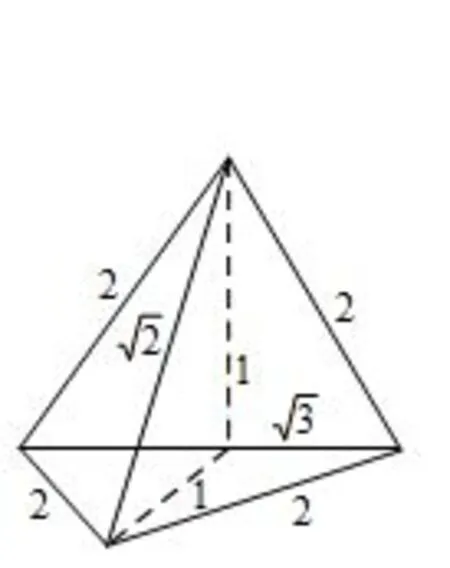
解析 由“高考秘诀”,三个视图都是三角形,则该几何体为三棱锥.由该几何体的三视图还原三棱锥的直观图,易知底面与一个侧面垂直,如图所示.且底面积为高为1,所以该几何体的体积为

根据“高考秘诀”,一般可以先由俯视图确定几何体底面的形状,俯视图通常情况下与几何体底面全等,再由正(主)视图、侧(左视图)视图、俯视图确定其它顶点的位置,从而画出原几何体的直观图.
方法 2.切割式—补外壳,再切割
例2(2014年全国I第12题)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )

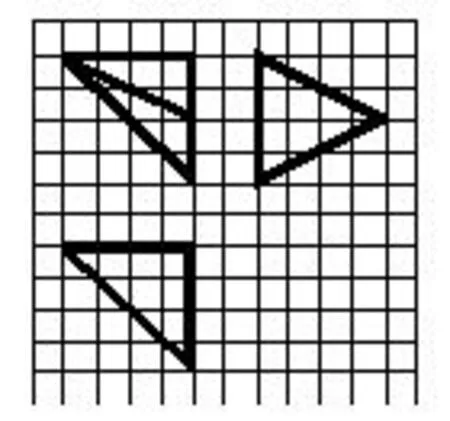

解析 认真分析三视图,你会发现它们的横边,竖边均为4,所以猜测此几何体寄居在正方体内;故先画正方体,根据三视图(先俯视图,后正视图、侧视图)找出满足题意的直观图,该几何体是如图所示的棱长为4的正方体内的三棱锥E-CC1D1(其中E为BB1的中点),其中最长的棱为
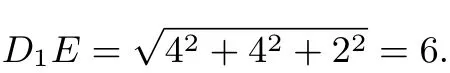
故选B.
变式2(2017年北京文科第6题)某三棱锥的三视图如图所示,则该三棱锥的体积为( ).
A.60 B.30 C.20 D.10


解析 认真分析三视图,发现该几何体的正视图的横边为5,竖边为4,侧视图的横边为3,所以猜测此几何体寄居在长方体内;故先画长方体,根据三视图(先俯视图,后正视图、侧视图)找出满足题意的直观图,该几何体是如图所示的长为5、宽为3、高为4的长方体内的三棱锥S-ABC,

若能在三视图中发现原几何体是由我们熟悉的几何体如正方体、长方体、直三棱柱等进行切割加工而成的,即原几何体“寄居”在这一“母体”内,则可以先由各个视图的外形确定其外壳,再由各个视图内的有关线段确定其加工的过程,从而确定原几何体的形状.特别注意是,在补形后的三视图所对应的几何体中,抓住关键点对应的投影点.
方法 3.组合式—先猜想,再验证
例3(2016年新课标全国II文科第7题)如图是圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为().
A.20π B.24π C.28π D.32π

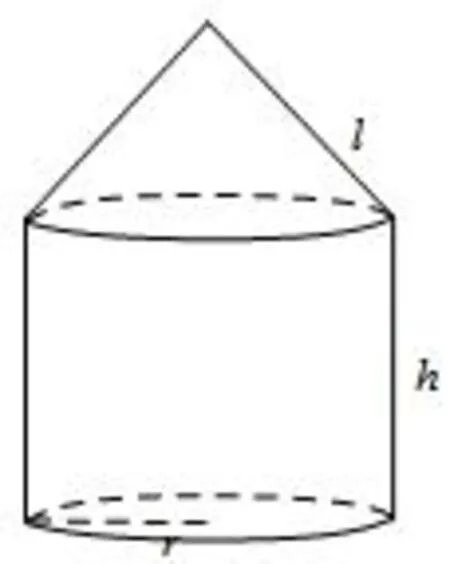
解析 该几何体为组合体,上面是圆锥,下面是圆柱,如图所示.设圆柱底面圆半径为r,周长为c,圆锥母线长为l,圆柱高为√h.由三视图得:r=2,c=2πr=4π,由勾股定理得,l
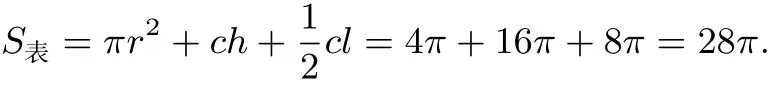
故选C.
变式3(2014年浙江理科第3题)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )
A.90cm2B.129cm2C.132cm2D.138cm2

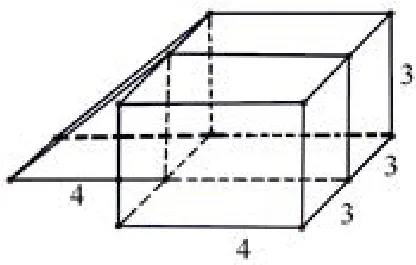
解析 由三视图可知该几何体由一个直三棱柱与一个长方体组合而成(如图),其表面积为

+2×4×3+2×4×6+3×6=138(cm2)
所以选择D.
对于组合体问题,最好能根据三视图的性质,猜想组成组合体各个部分的几何体形状,然后加以验证,从而得到原几何体的直观图,解答时将其分解为若干个简单几何体,然后再根据“高考秘诀”,各个击破.
三视图的实质是从正、侧、俯三个角度平行的投影几何体,得到的投影图;三视图还原出几何体直观图的高考题目中,培养学生构造正方体或长方体为母体的解题意识很重要,这样可以化陌生为熟悉,体现等价转化的数学思想.因此在掌握三视图实质的同时,再注意培养构造正方体或长方体为母体的意识,就可以以不变应万变,自信面对高考.

