(2+1)-维Toda-like晶格方程的对称变换和精确解

吕 娜，张 静，邱旭东

(1.大连民族大学 理学院，辽宁 大连 116650；2.北方民族大学 数学与信息科学学院，宁夏 银川 750021)

1 引论

微分差分方程存在于很多领域，并具有广泛的应用，例如计算机科学、生物数学、经济学、组合学、数学物理、离散几何、量子物理，等等。对于微分差分方程的研究最初是从Fermi等人在1950年的工作开始的。1991年，D. Levi和P. Winternitz[1]将李群方法推广到离散方程，并得到了这些方程的对称。近来科学家们对于微分差分方程的对称性质和构造精确解以及相应的物理现象愈发感兴趣，许多有效的分析方法相继产生[2-5]。2005年，楼森岳[6]在CK直接法的基础上巧妙地构造了一种修正的直接法，称为“楼直接法”，该方法不涉及群论思想，结果形式简单，易于使用。

楼直接方法的主要思想为：对于给定的非线性微分方程

F(xi,u,uxi,uxixj,…,)=0,i,j=1,2,…,n,

(1)

设方程(1)具有如下形式的解

u(x1,x2,…,xn)=W(x1,x2,…xn,U(ξ1,ξ2,…ξn))。

(2)

式中：ξ1是(x1,x2,…,xn)的函数，且U(ξ1,ξ2,…,ξn)满足与(1)形式相同的另一个方程

F(ξi,U,Uξi,Uξi,ξj,…,)=0,i,j=1,2,…,n。

(3)

将(2)代入到(1)，并结合(3)进行整理和化简，得到一个关于W和ξi的确定方程组。通过逐步化简来求解这个方程组，从而确定W和ξi的具体表达式，进而通过关系式(2)得到方程(1)的对称变换。本文主要利用楼直接方法研究一个微分差分方程的对称变换，并给出该方程的新精确解和数值算例。

2 (2+1)-维Toda-like晶格方程的对称变换

考虑如下的(2+1)-维Toda-like晶格方程[7]

(4)

式中：vn=vn(x,t)。引入变换

(5)

则方程(4)变为

(6)

为了获得方程(6)的对称变换，令

un=A+B·U(n,ξ,τ)。

(7)

式中：A、B、ξ和τ都是关于n、x、t的函数。令U(n)≡U(n,ξ,τ)，使其与晶格方程(6)有相同的形式，但关于新的独立变量ξ,τ，有

U(n)ξτ=U(n)τ(2U(n)-U(n-1)+U(n+1))。

(8)

将(7)式带入方程(6)，然后利用(8)消去U(n)ξτ，得到

B(n,x,t)ξtξxU(n)ξξ+B(n,x,t)τtτxU(n)ττ+V1(n,x,t,U(n-1),U(n),U(n+1),U(n)ξ,U(n)τ)=0。

(9)

式中：V1是一个与U(n)ξξ,U(n)ττ无关的复杂函数。方程(9)对于任意解U成立，当且仅当U的各阶导数项的系数为零。从方程(9)可以看出ξtξx=0,τtτx=0,不失一般性，假设

ξ=ξ(n,x),τ=τ(n,t)，

(10)

将(10)代入方程(6)，有

B(n,x,t)tξxU(n)ξ+V2(n,x,t,U(n-1),U(n),U(n+1),U(n)τ)=0。

(11)

式中：V2是一个与U(n)ξ无关的函数。消去U(n)ξ的系数，可以看出B(n,x,t)与t无关，设B(n)=B(n,x)，所以(7)可以化简为

un=A(n,x,t)+B(n)·U(n,ξ(n,x),τ(n,t))。

(12)

下面将(12)代入晶格方程(6)中，由于U(n),U(n-1),U(n+1)是方程(8)的任意解，收集U(n),U(n+1),U(n-1)和其导数项的系数，可得关于可微函数A,B,ξ和τ的确定方程组

τt[2A(n)B(n)-A(n-1)B(n)-A(n+1)B(n)-B(n)x]=0,

B(n)τt[ξx-B(n-1)]=0,B(n)τt[ξx-B(n+1)]=0,2B(n)τt[ξx-B(n)]=0,

B(n-1)At=0,B(n)At=0,B(n+1)At=0,

A(n)xt-2A(n)tA(n)+A(n)tA(n-1)+A(n)tA(n+1)=0。

(13)

式中：A(n)=A(n,x,t)。

求解上述方程组得到

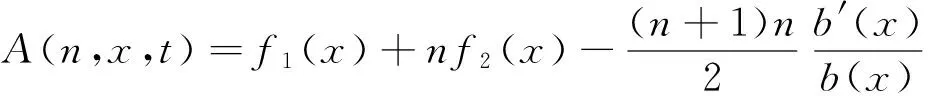
(14)

式中：f1(x),f2(x),b(x),h1(n),τ(n,t)是任意函数；n是任意常数。

结合(14)式，(7)化为

(15)

因此得到了关于Toda-like晶格方程的一个定理。

定理1 如果U(n)=U(n,x,t)是方程(6)的一个解，那么由(15)确定的un也是其一个解。

利用文献[8]中的方法，获得方程(6)的一个双曲函数解，

(16)

式中：φn=dn+kx+G(t)+c，且d,k,c,δ是常数，F(x),G(t)是任意函数。

根据定理1，

(17)

是方程(6)的一个新的类孤子解，其中

(18)

3 数值算例

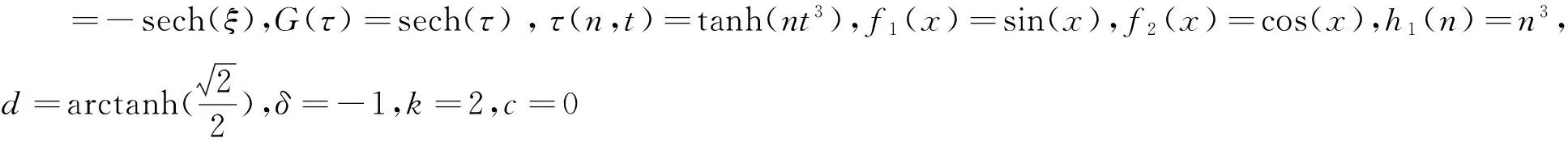
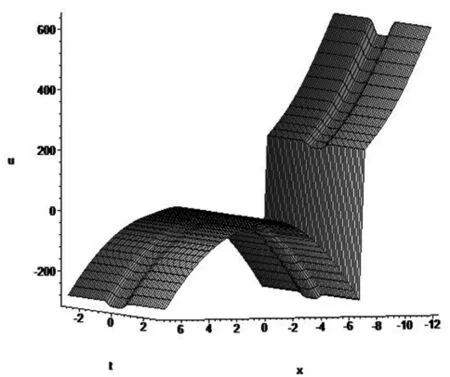
图1 类孤子解(17)在n=5时的图像

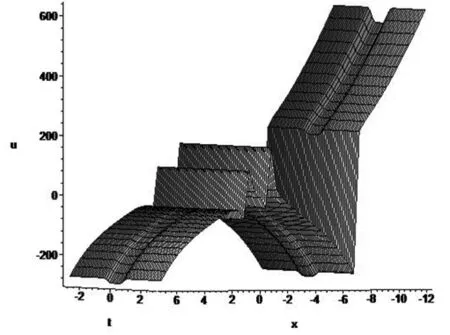
图2 类孤子解(17)在n=5时的图像

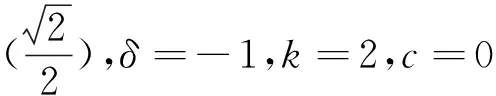
图3 类孤子解(17)在n=3时的图像

图4 类孤子解(17)在n=7时的图像

4 结 语

本文利用楼直接法得到了(2+1)-维Toda-like晶格方程的对称变换，并给出这个方程一个新的类孤子解。若想直接获得微分差分方程带有丰富任意函数的精确解，往往计算过程比较复杂，而借助于对称变换则可以较轻易地达到这个目的。因此对称变换是获得微分差分方程丰富精确解的有效工具。

[1] LEVI D, WINTERNITZ P. Continuous symmetries of discrete equations[J]. Physics Letters A, 1991, 152(7): 335-338.

[2] CHOU K S, QU C Z. Generalized conditional symmetries of nonlinear differential- difference equations [J]. Physics Letters A, 2001, 280(5): 303-308.

[3] SHEN S F. Clarkson-Kruskal direct similarity approach for differential- difference equations [J]. Commun. Theor. Phys.(Beijing, China), 2005, 44: 964-966.

[4] SAHADEVAN R, KHOUSALYA S, DEVI L N. Nonlocal symmetries and recursion operators: Partial differential and differential-difference equations[J]. Journal of mathematical analysis and applications, 2005, 308(2): 636-655.

[5] LI H J, WANG D S, WANG S K, et al. On geometric approach to Lie symmetries of differential-difference equations[J]. Physics Letters A, 2008, 372(37): 5878-5882.

[6] LOU S Y, MA H C. Non-Lie symmetry groups of (2+1)-dimensional nonlinear systems obtained from a simple direct method[J]. Journal of Physics A: Mathematical and General, 2005, 38(7): L129.

[7] MARTINA L, LAFORTUNE S, WINTERNITZ P. Point symmetries of generalized Toda field theories: II. Symmetry reduction[J]. Journal of Physics A: Mathematical and General, 2000, 33(36): 6431-6446.

[8] ZHANG S, ZHANG H Q. Variable-coefficient discrete tanh method and its application to (2+1)-dimensional Toda equation[J]. Physics Letters A, 2009, 373(33): 2905-2910.