基于优化调度的用户侧电池储能配置及控制方法

林俊豪，古雄文，马 丽



基于优化调度的用户侧电池储能配置及控制方法

林俊豪，古雄文，马 丽

（珠海派诺科技股份有限公司，广东 珠海 519000）

为提高用户侧电池储能系统的经济性及使用寿命，提出一种基于能量优化调度的储能配置及控制方法。首先，建立用户侧储能应用的成本及收益的经济性分析模型，综合考虑电池容量在不同最大放电深度下的衰减特性，以及负荷与可再生能源发电的不确定性，得到净收益最佳的储能容量配置方案。其次，在运行阶段，采用模型预测控制进行能量管理，跟踪设备出力变化，求解系统的最优调度决策，以保证用户收益及电池循环寿命。算例分析比较了数种类型电池，包括梯次利用电池的经济性，体现了所提储能联合规划与运行方法对优化用户侧储能经济价值的重要性。

用户侧储能；电池储能系统；优化调度；容量配置；经济性分析

分布式储能是构建智能电网与能源互联网的关键元素[1-2]。用户侧电池储能系统是安装于配网侧或终端电力用户的分布式储能装置，可提供削峰填谷、可再生能源配比、后备电源、调频调压等电能服务，提高供电质量及可靠性，并带来经济效益[3]。

用户侧电池储能的应用需要解决经济性及使用寿命的问题，现有研究工作对此问题的探讨可归纳为以下3个方面。①储能容量配置优化与经济性分析：通过建立用户侧储能应用的成本收益分析模型，检验储能投资的经济性，确定最佳的电池储能配置与运行方案[4]。现有工作主要考虑的收益类型包括削峰填谷及需量控制；在成本计算方面，现有工作主要考虑电池的投资成本、运行成本以及运行寿命[4-6]，较少有研究考虑运行期内电池容量衰减导致的成本或收益变化。②系统能量管理与优化控制：在储能系统接入后，一方面，需要考虑与电网及终端用户系统的其它设备，如分布式可再生能源发电、负荷等，共同协调运行，以优化电池储能的实际收益[7-8]。另一方面，需要考虑对多个储能系统或模组间的充放电功率分配及均衡控制，从而优化电池效率及寿命[9-10]。③储能应用领域的拓展：通过增加用户侧电池储能系统的功能与服务类型，提高电池储能应用的收益。例如，利用数据中心的后备电源提供削峰填谷服务[11]，集聚分布式电池以提供需求响应、频率调节服务[12]等。

在以上研究范畴之内，本文重点讨论面向单个终端电力用户，如工商企业、数据中心、家庭等的电池储能系统优化配置及控制方法，从而为用户提供经济性最优的电池储能投资及运行策略。

在规划阶段，对储能系统的容量和额定功率配置进行优化非常重要。优化配置保证了储能系统与用户的用电规模相匹配，使储能在投入运行后，可实现最佳的经济效益，不出现容量、功率的缺配、超配情况。这要求优化模型对规划和运行阶段进行综合考虑，才能使规划阶段对储能经济性的预估尽量接近未来的实际运行结果，从而保障用户的储能投资的收益可靠性。

然而，在现有关于储能优化配置的研究工作中，虽然大部分文献会在规划模型中考虑系统的运行情况，但规划模型中对复杂多样的运行情况的简化可能会使得预期的收益分析结果在实际运行中并不可达。文献[4]提出的经济性分析模型中，以电池的全寿命周期进行成本及收益折算，但对收益估算方法过于简化，不考虑系统可能的运行情况，可能造成收益估算结果与实际偏差较大。文献[5]对梯次利用电池在快速充电站应用的经济性进行了分析，虽然其通过估算梯次利用电池的容量衰减来预测系统的运行期，但并未将容量衰减造成的成本或收益变化计入规划模型中。文献[6]使用二层规划方法，上层模型优化储能容量配置，下层模型优化储能运行收益，但没有考虑在运行期间电池容量的逐渐衰减带来的收益损失。

用户侧电池储能能量管理的研究工作的主要目的为优化储能应用的经济性及电池的整体寿命。考虑电力市场机制和电池的循环寿命模型，文献[7]提出了电池储能系统参与频率调节服务的最优运行策略。文献[8]采用分层控制架构，提出一种整合多个分布式电池储能系统的能量管理方法，使各储能系统动态响应电网调度信号及电力市场信号进行充放电，同时维护其电池寿命。文献[9]研究多个分布式储能系统的功率分配策略，考虑各个储能系统的能量状态和效率的差异，使多个储能系统总体的能量效率得到优化。文献[10]对异质电池系统之间的荷电状态均衡问题进行深入探讨，提出了一种新的模组分布式均衡策略，以优化异质电池的整体容量。本文借鉴现有的能量管理工作，着重研究对单个电力用户的储能经济性优化方法，同时解决负荷及可再生能源发电的不确定性，以保证所配置的电池储能系统得到高效利用。

基于以上分析，本文在现有的规划模型基础上，提出一种基于能量优化调度的储能配置及控制方法，综合设计储能系统的规划与运行阶段的优化模型，从而提升储能应用全周期的经济最优性。本文的贡献如下：①综合分析储能系统规划与运行阶段的异同，将运行阶段中直接影响成本及收益的因素计入规划模型中，使规划阶段的收益估算尽量接近实际运行时的收益；②考虑电池容量的动态衰减模型，在能量调度时对电池充放电曲线进行优化，在保证储能收益的同时，维护和延长电池的使用寿命；③为解决负荷及可再生能源发电的不确定性，在规划模型中采用随机优化方法，在运行模型中采用模型预测控制方法，保证经济性分析结果的准确性及实际运行收益。

1 系统框架与建模

1.1 系统框架

考虑单个终端电力用户系统，其结构如图1所示，系统中包含电网供电、本地负荷、可再生能源发电设备、电池储能系统。本文假设可再生能源发电设备和电池储能系统都配有相应的接入及潮流控制装置，可保证系统稳定运行，并接受调度指令实现功率控制。

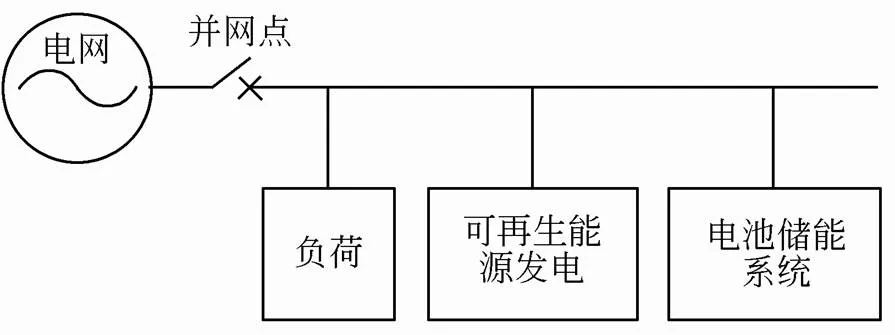
图1 单个终端电力用户系统的结构示意图

本文的优化问题框架如图2所示，采用优化调度方法来解决储能的配置与控制问题。规划与运行阶段的优化调度目标的组成互有异同，在第2节和第3节做具体说明。

图2 优化问题框架图

1.2 系统潮流模型

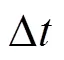
1.2.1 电池储能系统模型

为表述简洁，本文只考虑单个电池储能系统，但若需要，所提模型及方法可直接推广到多个储能系统。

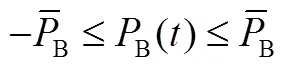
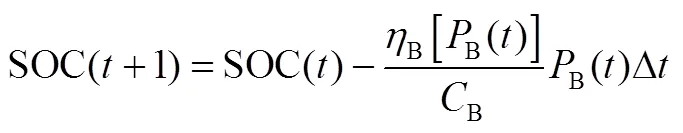
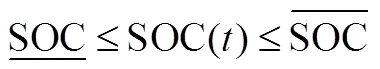
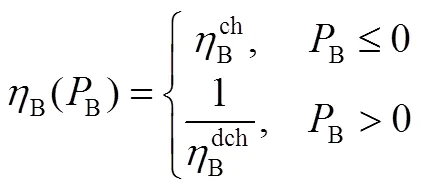
1.2.2 可再生能源发电模型

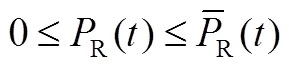
1.2.3 并网点功率平衡

2 电池储能的经济配置方法

对电池隧道储能系统进行容量和额定功率的经济性最优化配置，对成本和收入采用年化计算方式。

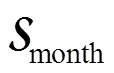
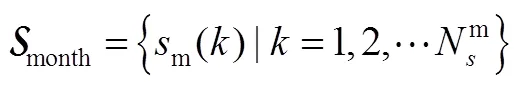
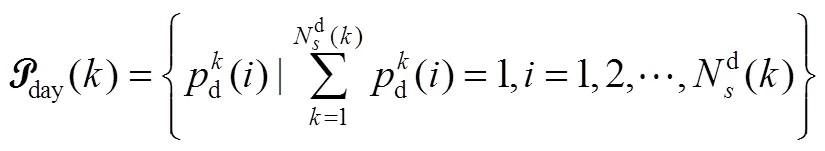
2.1 优化目标

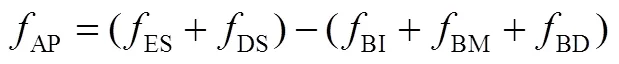
2.1.1 电度电费节省收益

储能可通过削峰填谷实现峰谷价差套利，从而减少电度电费，为用户带来收益。采用随机优化方法，每年电度电费节省收益的计算公式见式(13)

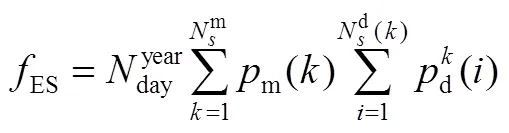
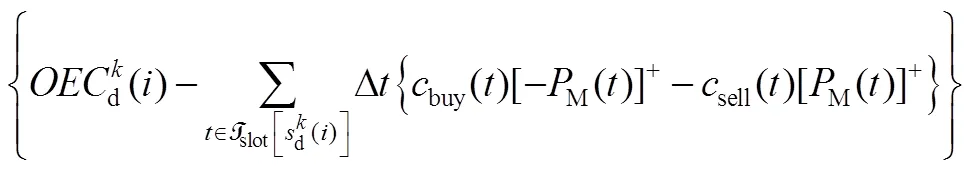
2.1.2 需量电费节省收益

储能可通过降低用户的负荷峰值，即最大需量，来减少用户的需量电费，为用户带来收益。采用随机优化方法，每年需量电费节省收益的计算公式见式(14)

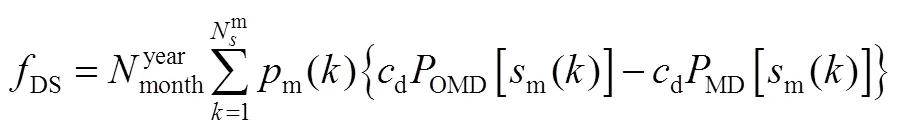
2.1.3 初始投资成本

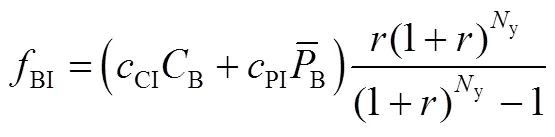
2.1.4 运维成本

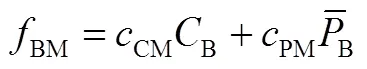
2.1.5 电池容量衰减成本

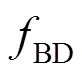
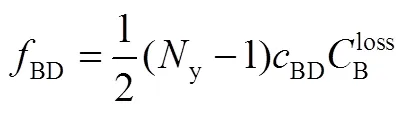
电池的循环寿命主要由放电深度及循环次数决定[5,7,13]。在最大放电深度（DOD，depth of discharge）一定的情况下，电池的容量衰减量与循环次数有近似线性关系[5]。本文采用的电池容量衰减的估算方法见式(18)

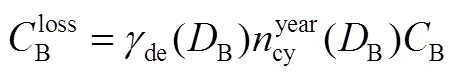
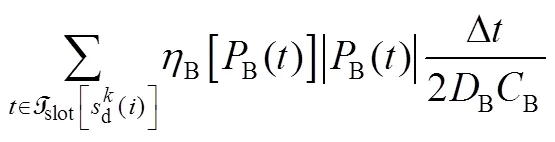
2.2 最优配置问题

结合以上模型，用于电池储能经济性分析的最优配置问题设计如式(20)～式(24)所示

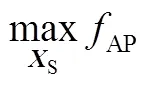
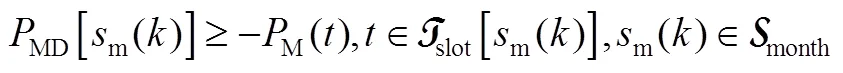
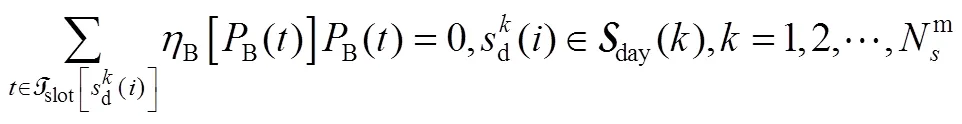
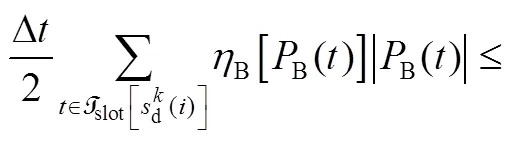
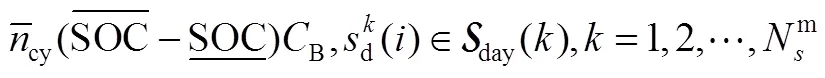
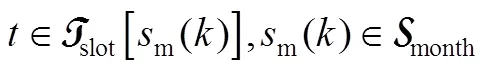
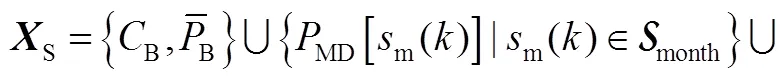
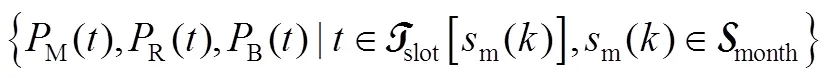
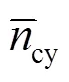
式(20)～式(24)定义的最优配置问题可转化为线性规划问题。通过求解最优配置问题，可得到经济性最优的电池储能系统的容量和额定功率配置，以及对应的最优每年净收益。

3 能量管理与控制方法

在系统运行时，对储能系统、光伏等设备的出力进行优化控制，在保证系统的电费开销最小的同时，维护电池循环寿命及平滑并网点的功率交换。

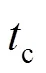
图3 模型预测控制的示意图

3.1 优化目标

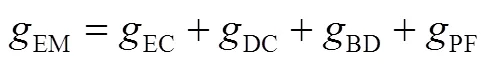
3.1.1 电度电费

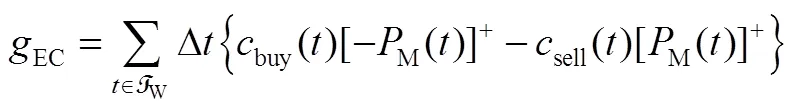
3.1.2 需量电费

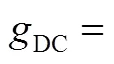
3.1.3 电池容量衰减罚函数

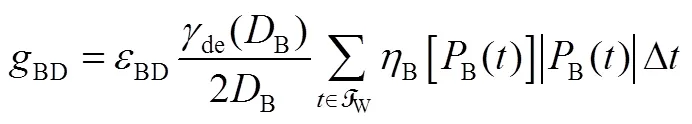
3.1.4 并网点功率波动平滑

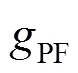
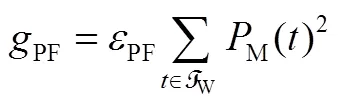
3.2 最优控制问题

结合以上模型，用于电池储能系统运行的最优控制问题设计见式(31)～式(35)

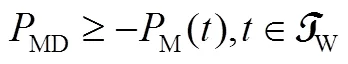
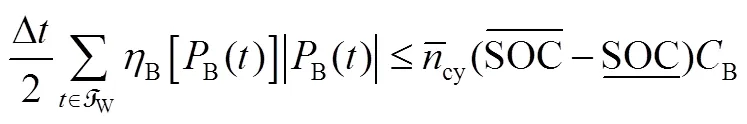
年份对于葡萄酒的重要性是不言而喻的。而符合葡萄酒“大年”的条件都在2015年一一组合，为此，本刊记者专访了波尔多列级庄联合会（UGCB）主席奥利维·贝尔纳（Olivier Bernard）。

式(31)～式(35)定义的最优控制问题可转化为二次规划问题。通过求解最优控制问题，可有效跟踪可再生能源发电和负荷的变化，得到系统总开销最小的运行策略。

4 算例分析

本节将分析对比常规铅炭电池、常规及梯次利用磷酸铁锂电池在用户侧储能应用的经济性，用数值结果检验本文所提的优化配置及控制方法的 效果。

4.1 模型参数说明

考察的三种电池的模型所需参数的设置如表1所示。电池参数值设定参考了电池厂家[14-15]和学术文献[5,16]资料。参考储能逆变器的厂家资料[17-18]，逆变器的转换效率设为0.97。

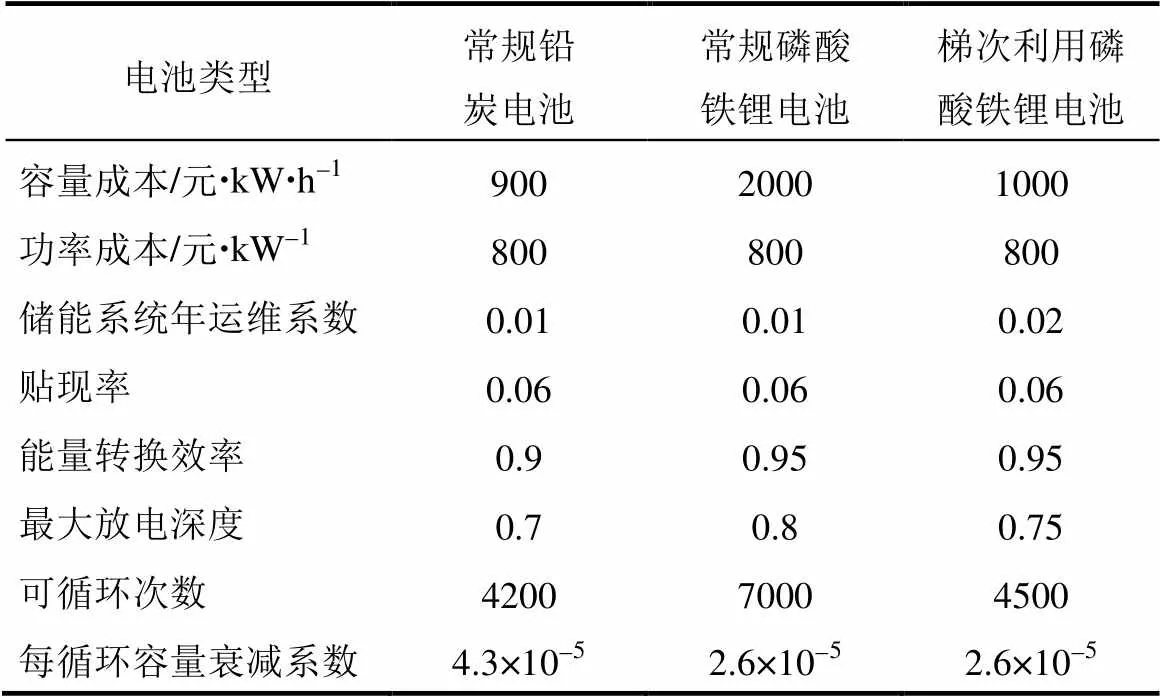
表1 3种电池的模型所需参数设置

实验所用的负荷数据取自广东省珠海市某工业企业于2015年及2016年两年的用电负荷数据，期间最大负荷为224 kW。对负荷数据采用聚类算法[19]，提取典型负荷曲线，作为优化模型的输入。所用的可再生能源发电数据来源为比利时电网公司Elia的光伏发电的公开数据[20]，用于仿真光伏发电的波动。对光伏数据等比例缩放至装机容量为56 kW，即与最大负荷的比例为25%。

用电价格采用广东省珠海市现行的1～10 kV大工业用电电价收费标准[21]，具体的需量电价和 峰谷平电度电价如表2所示。本实验假设用户的光伏发电全部自发自用，且只向电网购电，不向电网售电。

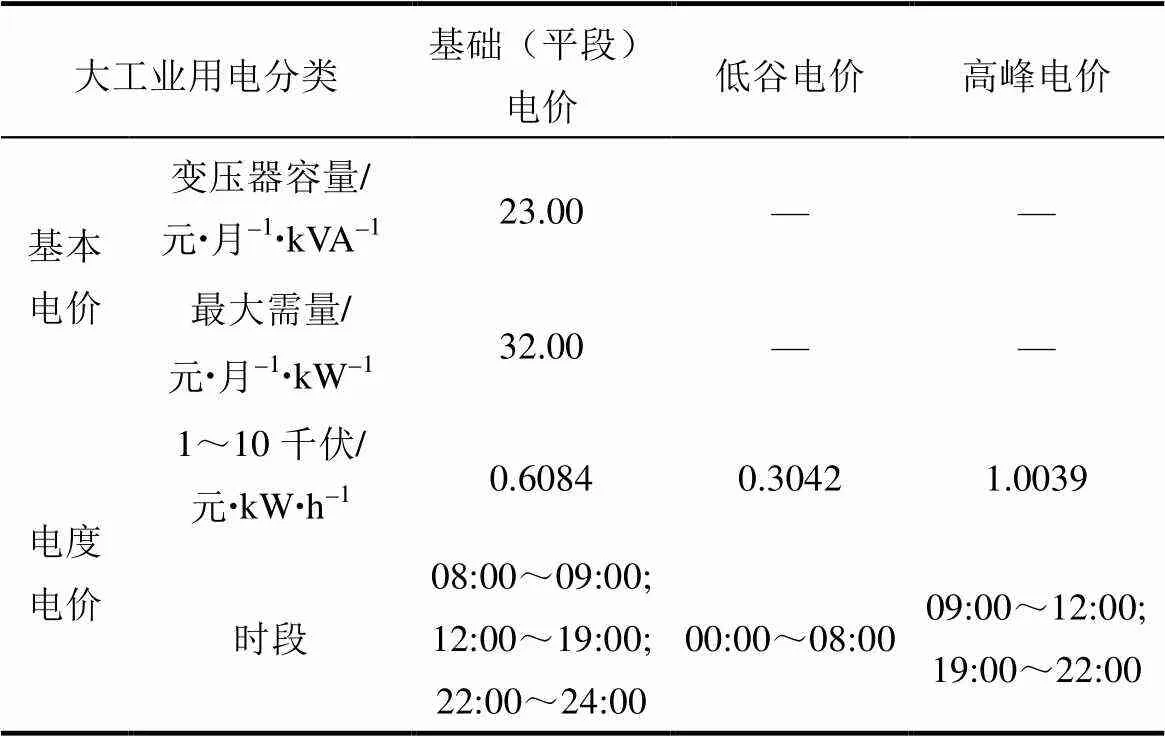
表2 广东省珠海市电价价目表

4.2 储能经济配置结果

将考察以下两种条件下分别的储能经济配置结果：①年均净收益最优；②在一定的投资回收期年限以内，年均净收益最优。

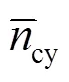
在仅考虑年均收益最优的情况下，电池储能经济配置的方案及收益如表4所示。其中，最后一行成本绩效指数为年均收益与年化成本的比值。由表4可见，常规铅炭电池和梯次利用磷酸铁锂电池的年均净收益明显高于常规磷酸铁锂电池。梯次利用磷酸铁锂电池在设置为每天循环一个周期以内时，年均净收益为所有配置方案中最高，表4中已加粗显示此配置方案。另一方面，对同一类型电池，当日循环周期限制增大时，年均净收益下降，但投资回收期也会缩短，表4中已加粗显示投资回收期最短的两组配置方案。可见，针对实验所考虑的电价曲线，电池每天的第一个循环周期的收益效率要明显高于第二个循环周期，但增加每日的循环周期可以加快成本收回的速度，这可能对一些用户在进行投资决策时存在吸引力。

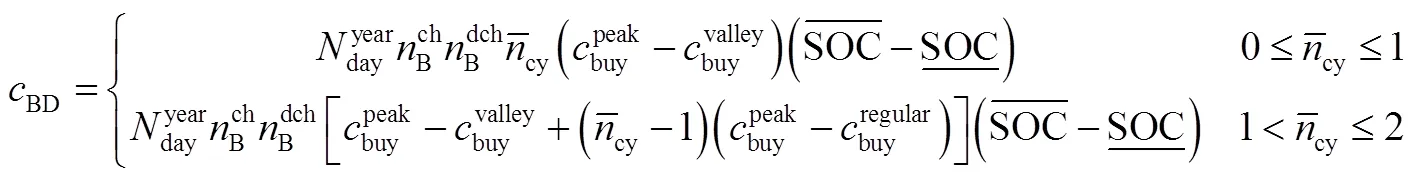
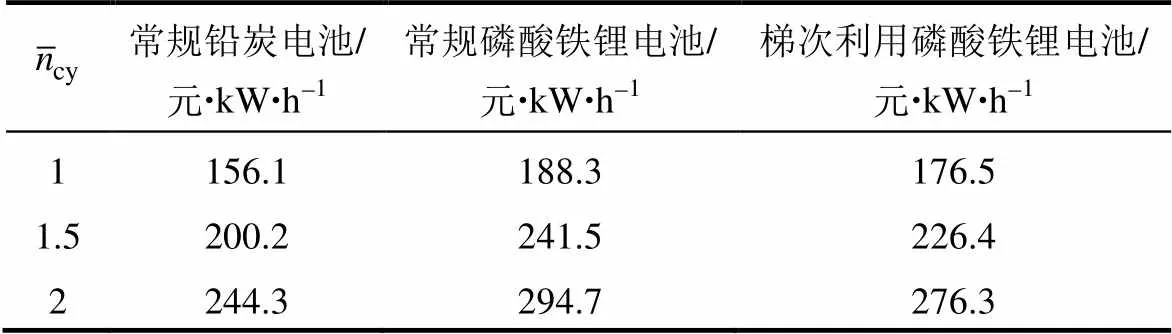
表3 电池单位容量衰减成本cBD取值表

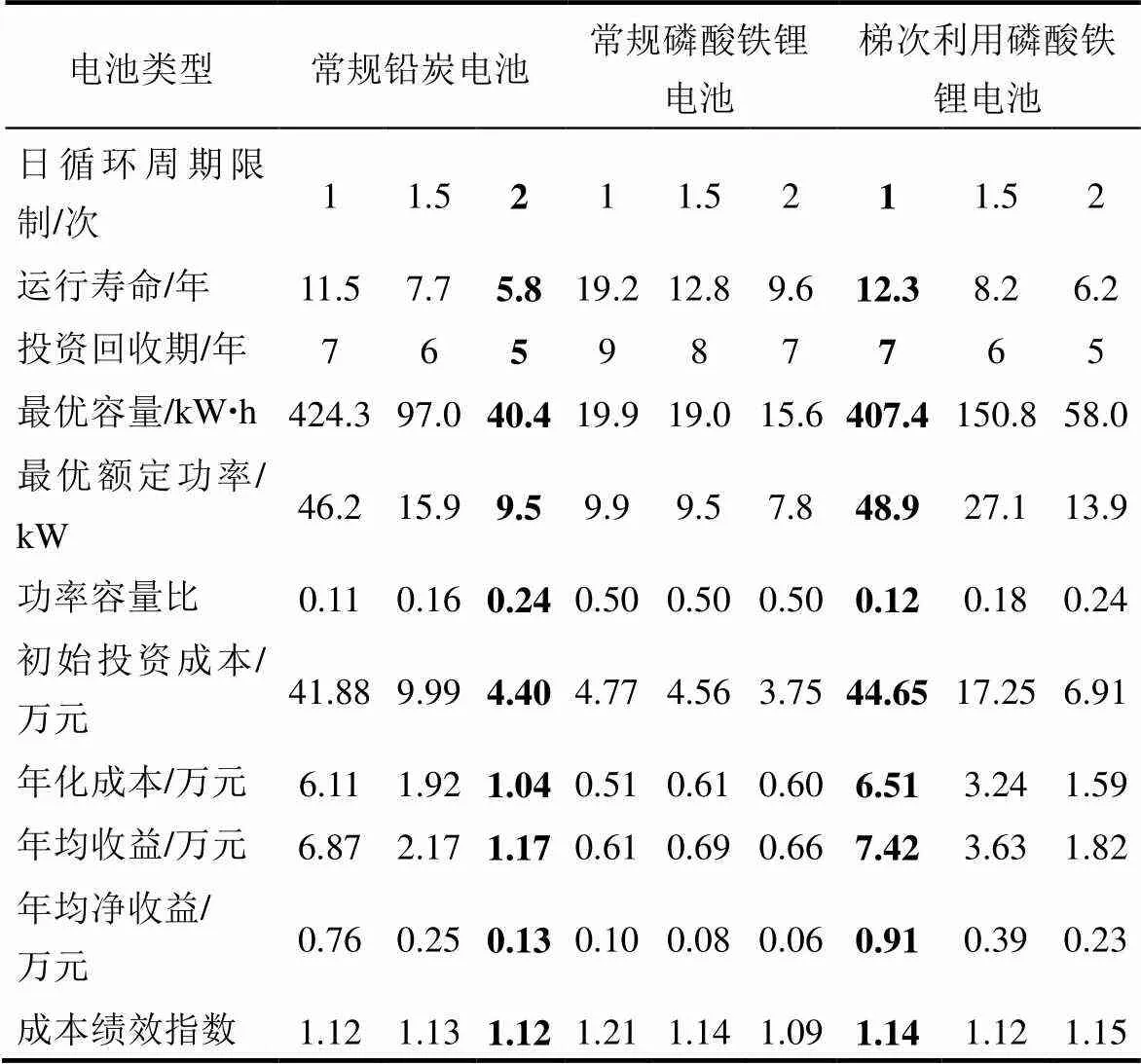
表4 年均净收益最优情况下的电池储能经济配置结果

基于表4的结果，限定投资回收期为5年以内，重新进行优化配置，结果如表5所示，由于常规磷酸铁锂电池不能在5年内收回成本，故没有列出其对应结果。由表5可见，年均净收益最高与成本绩效指数最高的两组配置方案均来自梯次利用磷酸铁锂电池，已加粗显示。对同一类型电池，当电池每日循环周期数限制在1.5次时，年均净收益最高，可见在加入了投资回收期的限制条件后，需要改变运行模式，找到最优的每日循环周期数，才能获得最大的年均净收益。

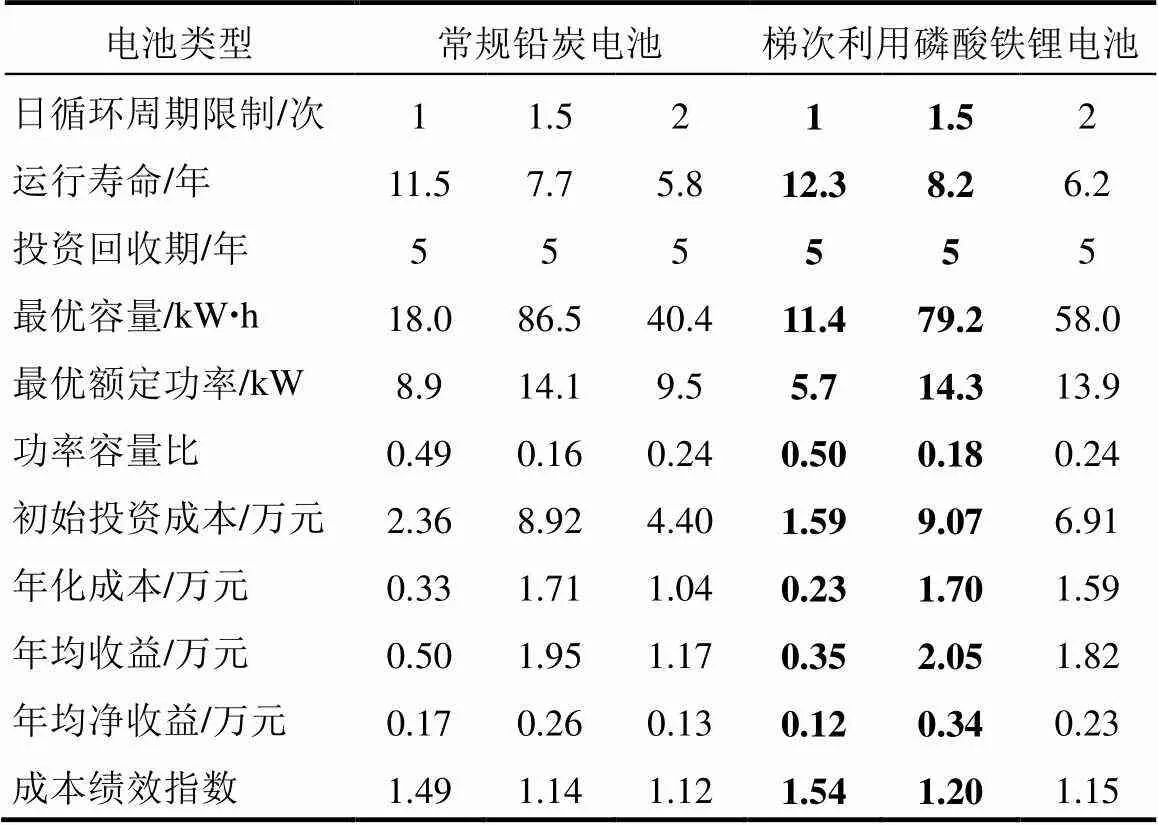
表5 限定投资回收期为五年的电池储能经济配置结果

综合以上储能经济配置结果及分析，对所考察的3种电池，以投资回收期、年均净收益、成本绩效指数三项指标评价，常规铅炭电池和梯次利用磷酸铁锂电池的经济性明显高于常规磷酸铁锂电池，这是由于目前常规磷酸铁锂电池的容量成本远高于另外两种电池；其次，尽管梯次利用磷酸铁锂电池的容量成本和运维成本都略高于常规铅炭电池，但由于梯次利用磷酸铁锂电池的能量转换效率和每循环容量衰减速率都较优于常规铅炭电池，故综合起来梯次利用磷酸铁锂电池的经济性要稍优于常规铅炭电池。

4.3 能量管理与控制结果

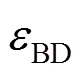
对每种电池储能配置方案，数值模拟运行一年，采用第3节提出的最优控制方法对系统进行能量管理与调度。根据系统运行曲线，统计储能收益，并与规划阶段中的收益对比，结果如表6所示。由表6可见，实际年运行收益与规划年均收益估算差距在2%～4%，表明所提储能配置方法可对收益有较准确的评估，优化配置结果较可靠。

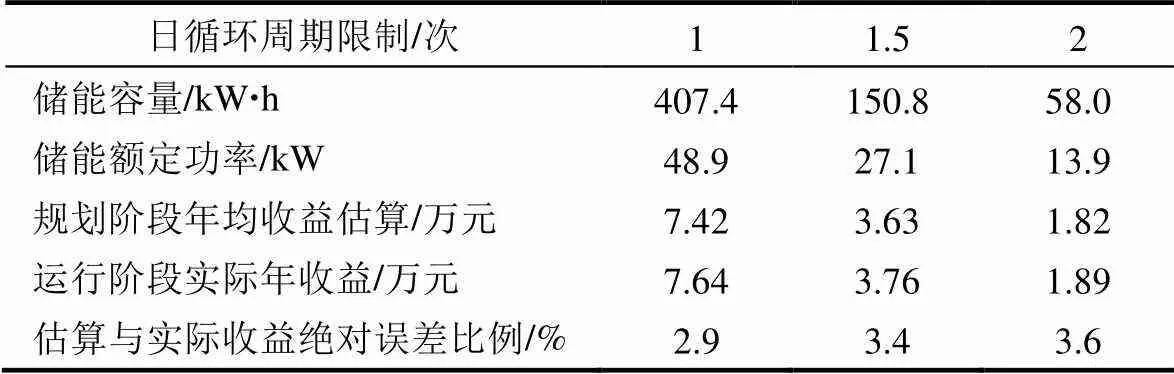
表6 梯次利用磷酸铁锂电池储能系统的运行收益

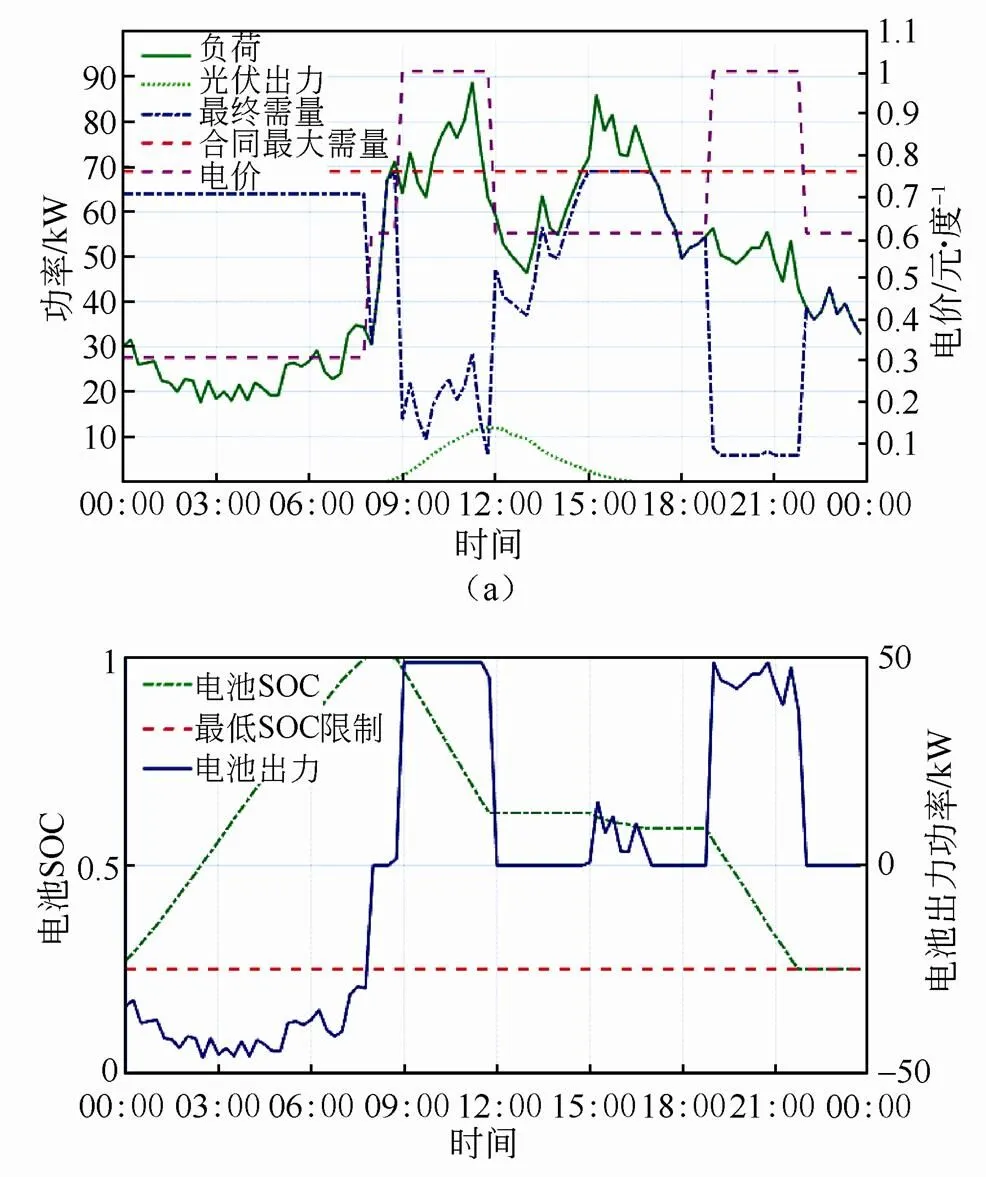
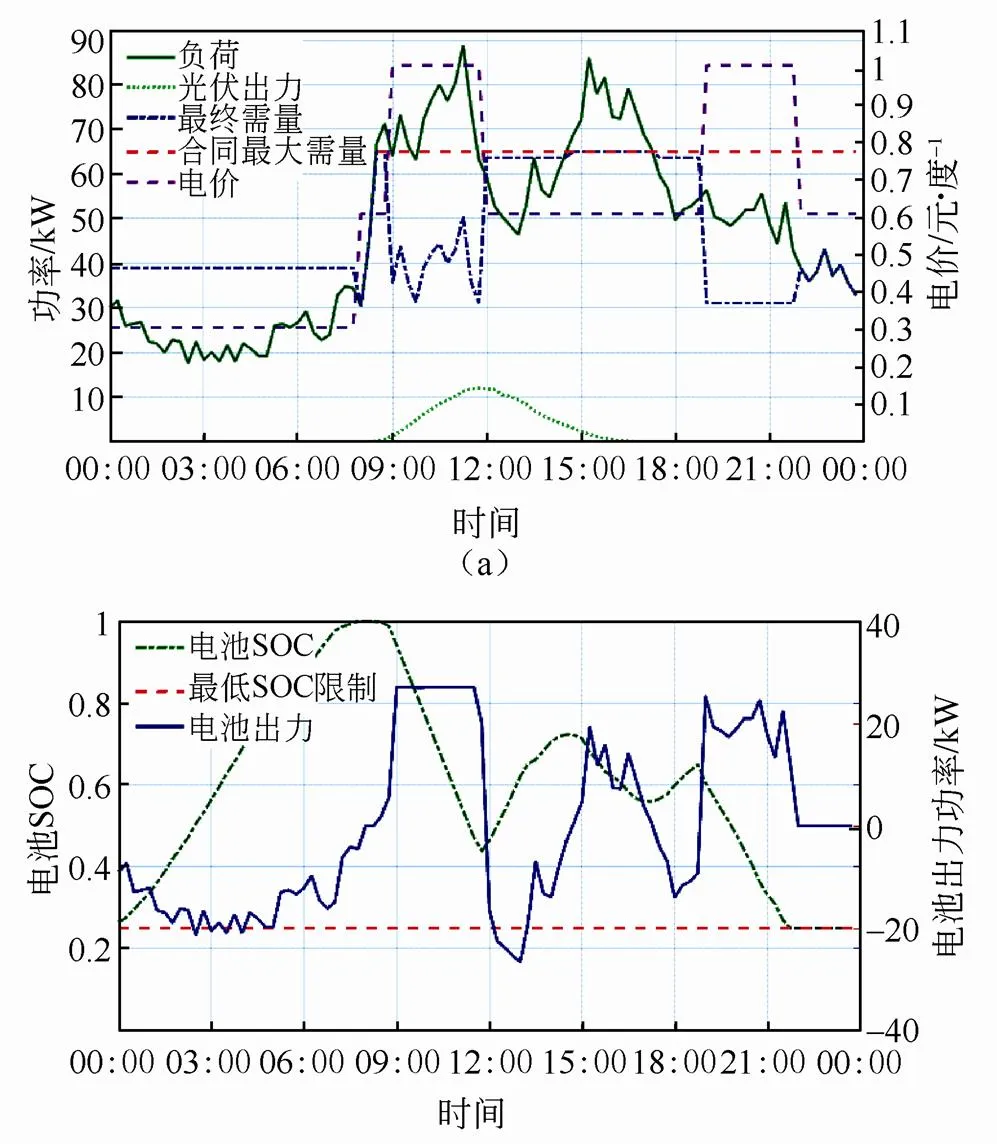
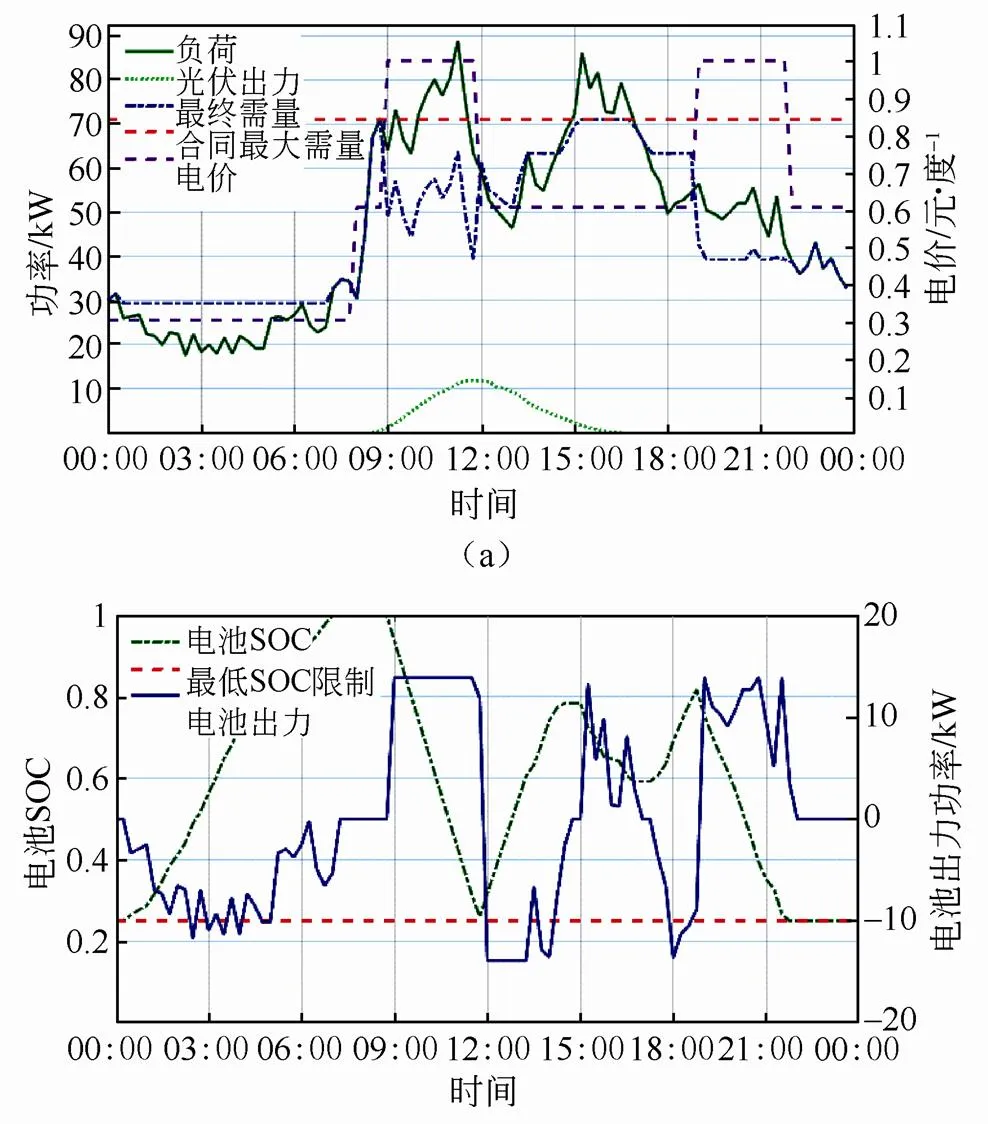
图4～图9展示了不同的电池每日循环周期限制下的系统运行曲线。对应的储能系统的配置见表6。图4和图5分别为日循环周期限制为1次时的夏季和冬季某天的系统运行曲线。图6和图7分别为日循环周期限制为1.5次时的夏季和冬季某天的系统运行曲线。图8和图9分别为日循环周期限制为2次时的夏季和冬季某天的系统运行曲线。图4～ 图9的每一个图中，图(a)展示了负荷、光伏出力和最终需量曲线，并给出了合同最大需量和电价曲线作为参考；图(b)展示了电池的SOC和出力曲线，并标示了最低SOC限制。

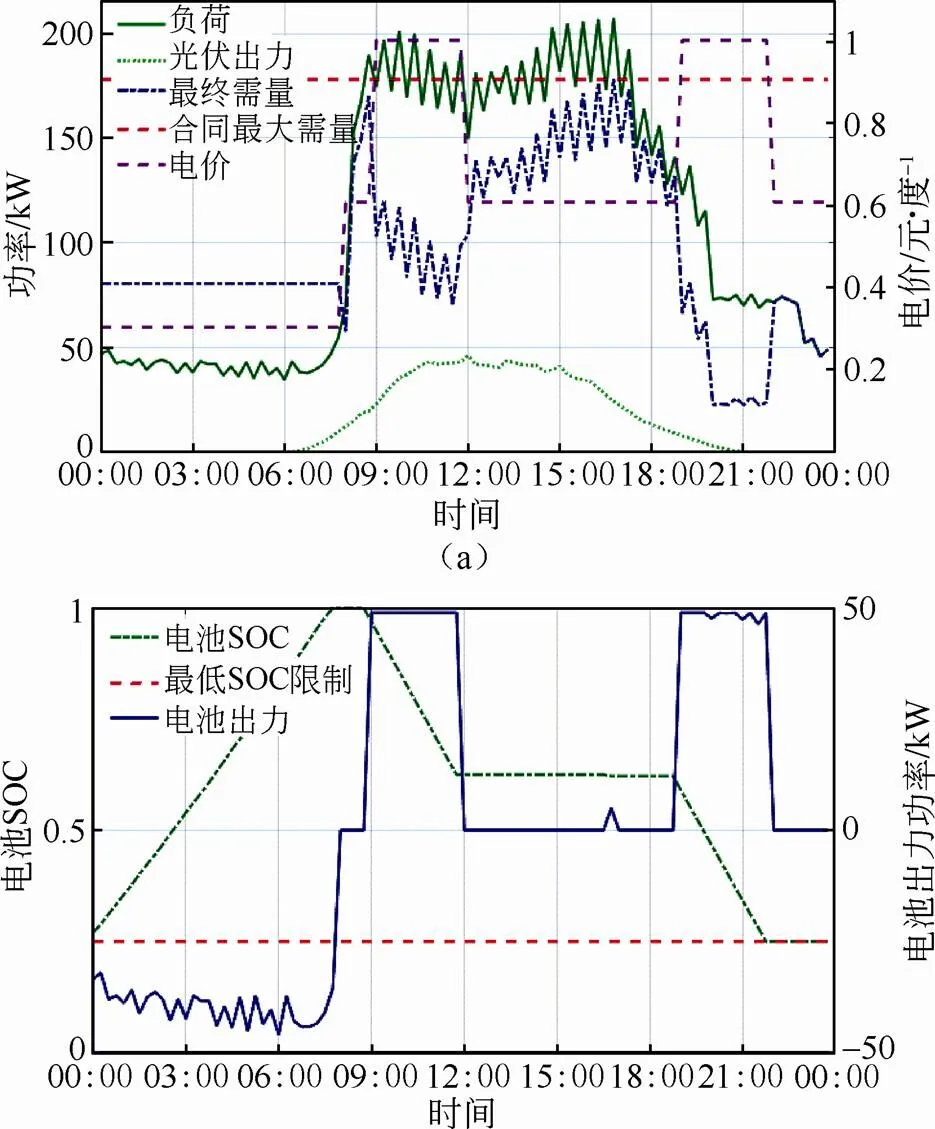
（b）

Fig.4 System operation profiles of one day in summer with the daily battery cycle limit equal to one

（b）

（b）

（b）

（b）

（b）

将图4～图9中各自的夏季与冬季的运行曲线进行对比，可见经过优化配置的储能系统，无论是在夏季负荷较高，还是在冬季负荷较低时，都能充分利用储能容量，进行相应次数的充放电循环，赚取削峰填谷收益。其次，所提最优控制方法可在不影响收益的情况下，尽量平滑最终需量曲线，亦即并网点功率交换曲线。

总结以上分析，本节通过数值实验，展示了所提基于优化调度的储能配置和控制方法可有效贯通储能系统规划和运行阶段，综合考虑两个阶段的异同，使用户侧储能应用得到最佳的投资回报。

5 结 论

本文提出了一种基于优化调度的用户侧储能配置及控制方法，对储能系统规划和运行阶段的优化模型进行统一设计，从而提高用户侧储能应用全周期的投资回报。在规划模型中，考虑了电池在不同充放电循环模式及最大放电深度限制下的收益变化，以更准确地评估储能收益，同时维护电池寿命。算例分析对常规铅炭电池，以及常规和梯次利用磷酸铁锂电池的储能应用经济性进行了对比，结论 如下。

（1）在本算例中，以回收周期及年均净收益为关键指标，分析得常规铅炭电池的经济性高于常规磷酸铁锂电池。

（2）系统运行实验结果表明，储能的实际年运行收益与规划阶段的年均收益估算误差在2%～4%以内，表明所提储能配置方法可对收益有较准确的评估，优化配置结果较可靠，所提能量管理与控制方法可调度储能系统以赚取最佳收益。

下一步工作将拓展所提优化框架，考虑多种类型储能共存及提供更多种电能服务，如频率调节等情况下的模型设计与求解方法。

[1] 国家能源局. 关于促进储能技术与产业发展的指导意见（征求意见稿）[Z]. 北京: 国家能源局, 2017.

[2] 慈松, 李宏佳, 陈鑫, 等. 能源互联网重要基础支撑: 分布式储能技术的探索与实践[J]. 中国科学: 信息科学, 2014, 57(6): 762-773.

CI Song, LI Hongjia, CHEN Xin, et al. The cornerstone of energy internet: Research and practice of distributed energy storage technology[J]. Science China: Information Sciences, 2014, 57(6): 762-773.

[3] 邢洁, 曹哲, 张怡, 等. 储能系统应用于用户侧的技术经济分析[J]. 电气应用, 2017, 36(1): 26-30.

[4] 薛金花, 叶季蕾, 陶琼, 等. 采用全寿命周期成本模型的用户侧电池储能经济可行性研究[J]. 电网技术, 2016, 40(8): 2471-2476.

XUE Jinhua, YE Jilei, TAO Qiong, et al. Economic feasibility of user-side battery energy storage based on whole-life-cycle cost model[J]. Power System Technology, 2016, 40(8): 2471-2476.

[5] 韩晓娟, 张婳, 修晓青, 等. 配置梯次电池储能系统的快速充电站经济性评估[J]. 储能科学与技术, 2016, 5(4): 514-521.

HAN Xiaojuan, ZHANG Hua, XIU Xiaoqing, et al. Economic evaluation of fast charging electric vehicle station with second-use batteries energy storage system[J]. Energy Storage Science and Technology, 2016, 5(4): 514-521.

[6] 朱佳明, 刘斌, 谢海远, 等. 基于二层规划的用户侧储能容量配置和最优运行策略分析[J]. 南方电网技术, 2016, 10(10): 43-50.

ZHU Jiaming, LIU Bin, XIE Haiyuan, et al. Energy storage capacity allocation and optimal operation strategy analysis at demand side based on bilevel programming[J]. Southern Power System Technology, 2016, 10(10): 43-50.

[7] HE G, CHEN Q, KANG C, PINSON P, XIA Q. Optimal bidding strategy of battery storage in power markets considering performance-based regulation and battery cycle life[J]. IEEE Transactions

on Smart Grid, 2016, 7(5): 2359-2367.

[8] ZHANG T, CHEN S X, GOOI H B, et al. A hierarchical EMS for aggregated BESSs in energy and performance-based regulation markets[J]. IEEE Transactions on Power Systems, 2017, 32(3): 1751-1760.

[9] CHOI J Y, CHOI I S, AHN G H, et al. Advanced power sharing method for energy efficiency improvement of multiple battery energy storages system[J]. IEEE Transactions on Smart Grid, 2017: doi:10.1109/TSG. 2016.2582842.

[10] WANG L Y, WANG C, YIN G, et al. Balanced control strategies for interconnected heterogeneous battery systems[J]. IEEE Transactions on Sustainable Energy, 2016, 7(1): 189-199.

[11] SHI Y, XU B, ZHANG B, et al. Leveraging energy storage to optimize data center electricity cost in emerging power markets[C]// Proceedings of ACM e-Energy, 2016.

[12] LIN J, LEUNG K C, LI V O K. Optimal scheduling with vehicle-to-grid regulation service[J]. IEEE Internet of Things Journal, 2014, 1(6): 556-569.

[13] XU B, OUDALOV A, ULBIG A, et al. Modeling of lithium-ion battery degradation for cell life assessment[J]. IEEE Transactions on Smart Grid, 2017: doi:1109/TSG. 2016.2578950.

[14] 圣阳电源. 铅炭电池FCP-1000规格特性表[EB/OL]. [2017/07/18]. http://www.sacredsun.cn/uploads/FCP-1000.pdf.

[15] 比亚迪新能源. 电池储能技术小常识[EB/OL]. [2017/07/18]. http://www.bydenergy.com/BYDEnergy/pages_ch/news/Battery-xiaochangshi.htm.

[16] 廉嘉丽, 王大磊, 颜杰, 等. 电力储能领域铅炭电池储能技术进展[J]. 电力需求侧管理, 2017, 19(3): 21-25.

LIAN Jiali, WANG Dalei, YAN Jie, et al. The progresses of lead carbon battery technology for grid-scale energy storage[J]. Power Demand Side Management, 2017, 19(3): 21-25.

[17] 阳光电源. 储能逆变器[EB/OL]. [2017/09/06]. http://www. sungrowpower.com/index.php?s=/Home/business/product/id/35.html.

[18] 盛弘电气. 储能变流设备[EB/OL]. [2017/09/06]. http://www. sinexcel. com/pro_view-13.html.

[19] 张斌, 庄池杰, 胡军, 等. 结合降维技术的电力负荷曲线集成聚类算法[J]. 中国电机工程学报, 2015, 35(15): 3741-3749.

ZHANG Bin, ZHUANG Chijie, HU Jun, et al. Ensemble clustering algorithm combined with dimension reduction techniques for power load profiles[J]. Proceedings of the CSEE, 2015, 35(15): 3741-3749.

[20] ELIA. Solar-PV power generation data[EB/OL]. [2017/07/18]. http:// www.elia.be/en/grid-data/power-generation/Solar-power-generation-data/Graph.

[21] 广东省发展改革委员会. 广东省发展改革委关于调整销售电价等有关问题的通知[EB/OL]. [2017/07/18]. http://www.gddrc.gov.cn/ zwgk/ tzgg/jggg/201707/t20170714_401319.html.

Optimal sizing and control of demand-side battery energy storage system

LIN Junhao, GU Xiongwen, MA Li

(Zhuhai Pilot Technology Co. Ltd., Zhuhai 51900, Guangdong, China)

Battery energy storage is the building blocks of the Energy Internet. To improve the economy and battery life of the demand-side battery energy storage system (BESS), an optimal sizing and control method for the BESS is proposed based on an optimal scheduling approach. First, a cost-benefit analysis model is developed for evaluating the economy of demand-side energy storage. Accounting for the characteristics of battery capacity degradation under different depth of discharge (DOD) as well as the uncertainties of load and renewable generation, the optimal power and energy capacities of the BESS are determined by a stochastic scheduling method. For energy management, model predictive control is applied to adapt to the changes of the system conditions, and the profit generated by the BESS as well as the battery cycle life are optimized jointly. The proposed method considers the system operations in the planning model in order to give a more accurate evaluation of the revenues generated by the BESS. Case studies compare the economy of several types of battery energy storage including second-use batteries, and demonstrate the effectiveness of the proposed joint planning and operating method in optimizing the economic benefits of demand-side energy storage. Numerical results indicate that the economic benefits of new lead carbon batteries and second-use LiFePO4batteries outperform new LiFePO4batteries in terms of payback periods and annual profits.

demand-side energy storage; battery energy storage system; optimal scheduling; capacity sizing; economic analysis

TM 912

A

2095-4239（2018）01-090-10

10.12028/j.issn.2095-4239.2017.0144

2017-08-25；

2017-09-10。

广东省引进博士后资助计划。

林俊豪（1989—），男，博士，主要研究方向为电力系统优化与控制、能量路由、数学优化算法等，E-mail：linjh@pmac.com.cn。