有限元应力确定性模型在里石门拱坝中的应用

张 瑞，蔡爽龙，王浩军

（浙江省水利水电勘测设计院，浙江 杭州 310002）

1 问题的提出

里石门水库位于浙江省天台县境内始丰溪上。坝前正常高水位为176.00 m，校核洪水位为186.30 m，死水位为140.00 m，发电死水位为156.00 m。大坝为变半径变中心角混凝土双曲拱坝，最大坝高74.30 m，最大底宽15.50 m，坝顶宽度4.00 m，厚高比0.208，坝顶弧长265.50 m。圆弧半径 33.00 ～ 110.00 m，中心角度为 70° ～ 134°。

常见的大坝监测数学模型主要包括：统计模型、确定性模型和混合模型[1]。1955年，意大利的Faneli和葡萄牙的Roeha首次应用统计回归方法定量分析大坝的变形监测资料。1977年，Faneli又提出了大坝变形的确定性模型和混合模型，将理论计算值与实测数据结合起来。在我国，陆美霞、王小敏等使用有限元法建立了大坝变形的确定性模型[1]。

目前，针对大坝坝体应力的监测资料分析多以统计模型为主。根据里石门的应力监测资料实际情况，从1990年开始，应变计的电阻测值跳动幅度较大，测值不稳，存在较大误差，无法建立合理的应力统计模型。本文通过三维有限元方法，由水平位移统计模型分离出的水压分量位移，反演出大坝的弹性模量[2]，并应用反演出的弹性模量计算出大坝在不同水位和温度下的坝体应力，建立较合理的大坝应力确定性模型[3]。

2 坝体弹模参数反演

坝体任意一点的水平位移按成因可分为3个部分：水压分量、温度分量和时效分量。其中水压分量和温度分量占重要比重，本文也仅考虑水压、温度分量对坝体应力的影响。

将统计模型分离出的水压分量作用下水平位移作为反演的目标位移，通过常规反演法得到坝体的综合弹性模量为：左岸非溢流坝段1.92×104MPa，溢流坝段1.80×104MPa，右岸非溢流坝段 1.96×104MPa。采用反演参数后，6#（GL1 - 187测点）、12#（SL1 - 187测点）、18#（GL2 - 187测点）坝段正常蓄水位下有限元模型与统计模型水压分量位移见表1。

表1 正常蓄水位下有限元模型与统计模型水压分量位移表 mm

3 三维有限元数值模拟分析

3.1 模型的建立

坝址处河谷横断面呈U形，基岩为熔结凝灰岩。根据里石门水库大坝的实际尺寸以及弹性有限元理论，基岩区域沿水流方向的长度取为1倍坝宽，高度取为1倍坝高[4]。对基岩底部施加三向约束，基岩的上下游面及坝轴方向施加法向约束。在建立三维有限元模型时，坝体部分模拟溢流坝段、泄洪孔洞、排水廊道等重要结构，使最终计算结果能反映实际变形情况。在布置节点时，尽可能使测点作为节点。大坝的计算参数见表2。

单元采用6面体8结点和5面体6结点等参单元。拱坝及基岩整体模型共计有81 408个等参单元，127 249个节点，其中拱坝部分含有27 988个等参单元，33 819个节点。X方向指向下游为正，Y方向垂直向上为正。有限元计算模型见图 2 ～ 3。

表2 有限元计算参数表

图2 有限元计算整体模型图

图3 有限元计算坝体模型图

3.2 水压分量下应力数值模拟结果

根据监测资料分析表明，里石门拱坝呈良好的弹性工作状态，因此本次计算本构采用线弹性模型。在建立拱坝的主应力确定性模型时，考虑到坝肩和坝中是应力值较大区域，且实际拱坝也在此区域出现了多条裂缝，因此本文取高程185.00 m坝肩处和高程156.00 m拱冠梁处，作为应力模型的研究区域。

施加水压分量荷载时，坝前水位范围为156.00 ～185.00 m。限于篇幅，本文仅给出了176.00 m正常蓄水位下坝体位移等值线图和上下游面的第一、第三主应力等值线图（见图4 ～ 5）。其中为了显示清楚，取消下游支墩和牛腿的显示。

由图4可知，正常蓄水位下，坝体整体向内收缩，顺河向位移指向下游并呈辐射状分布，符合水压作用下拱坝变形一般规律。由图5可知，正常蓄水位下，坝体整体处于低拉应力状态，只在上游面坝底区域出现了较大的主拉应力，但范围极小，是典型的应力集中现象。主压应力最大值出现在下游面，最大主压应力为4.49 MPa，发生在坝底区域。

水压分量下库水位与主应力间的关系曲线见图6 ～ 7。

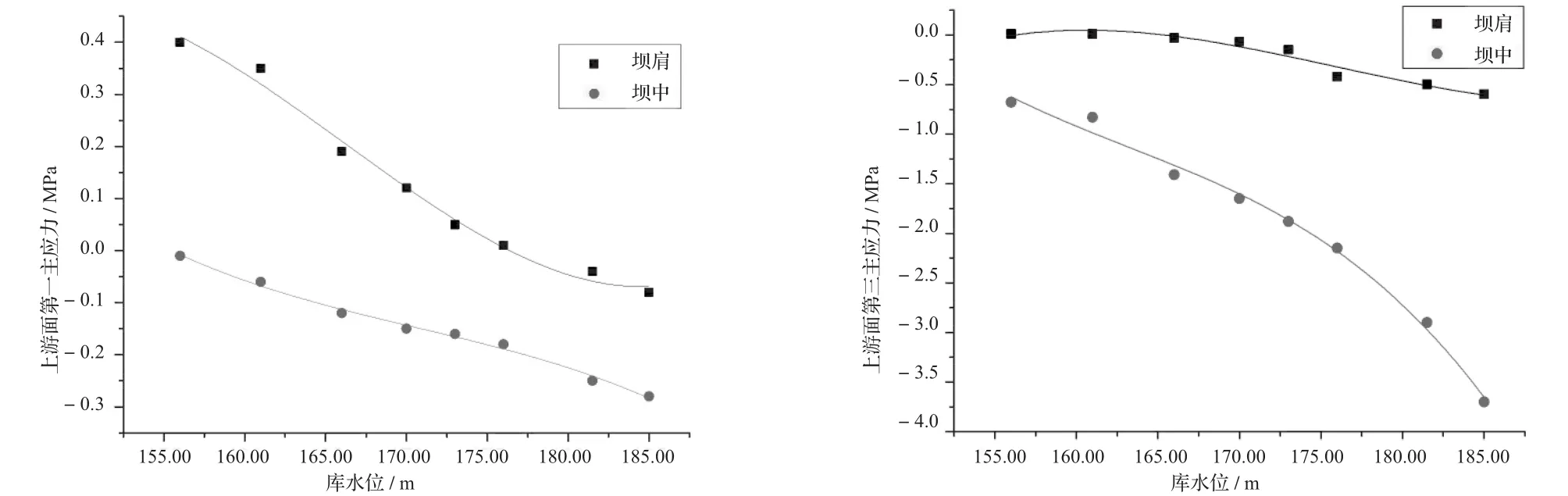
图6 上游面库水位与主应力的关系曲线图

图7 下游面库水位与主应力的关系曲线图

由图6可知，在坝体上游面，主拉应力值整体较小，随着水位的升高，坝肩、坝中处的主拉应力值逐渐降低；上游面主压应力值小于混凝土容许压应力，随着水位的升高，坝肩处主压应力值变化较小，坝中的主压应力值逐渐增大，在校核洪水位时达到3.29 MPa。

由图7可知，在坝体下游面，坝中处主拉应力较大，随着水位的升高，坝肩主拉应力值逐渐降低，坝中主拉应力值逐渐增大，在校核洪水位时达到1.18 MPa；随着水位的升高，坝肩、坝中处主压应力值逐渐增大，在校核洪水位时坝中主压应力值达到2.24 MPa。

3.3 温度分量下应力数值模拟结果

温度作用是拱坝设计中的一项主要荷载。随着坝内温度的变化，坝体发生变形，由于坝体嵌固于基岩而不能伸缩和移动，坝内便产生了温度应力。在计算温度应力时，考虑大坝的封拱温度，并根据水库上下游水位和水温分布，以及坝址多年平均气温，施加温度的外部边界荷载[6]。同时，实际监测资料表明，廊道内的气温也基本维持在一个固定区域内，因此也将廊道内温度作为坝体内部温度的边界条件，这样能更加真实地模拟坝体的温度分布规律。

本文给出了7月份（平均温度28 ℃）温度荷载下坝体位移等值线图和上下游面的第一、第三主应力等值线图（见图 8 ～ 9）。

图8 坝体7月份温度荷载下位移等值线图 单位：m

图9 坝体7月份温度荷载下主应力等值线图 单位：Pa

由图8可知，高温作用下大坝倾向上游变形，在靠近坝顶部分，温度变化的影响更为显著[5]，符合温度荷载下大坝变形的一般规律。由图9可知，在7月份，坝体上游面主拉应力最大值出现在坝中区域，最大值为1.40 MPa，上游面主压应力最大值出现在坝肩区域，最大值为0.60 MPa。坝体下游面主拉应力最大值出现在坝肩区域，最大值为0.90 MPa，下游面主压应力最大值出现在坝中区域，最大值为2.22 MPa。

取不同月份的多年平均气温作为大坝边界气温荷载，计算坝体应力，并建立主应力值与月份的对应关系曲线（见图 10 ～ 11）。

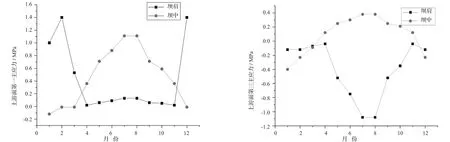
图10 上游面主应力值与月份的关系曲线图

图11 下游面主应力值与月份的关系曲线图

由图10 ～ 11可知：

（1）高温月份时：上游面坝中的拉应力较大，在7月份时达到最大值，坝中最大主拉应力为1.11 MPa；上游面坝肩处的压应力值较大，在7月份时达到最大值，坝肩最大主压应力为1.08 MPa；下游面坝中的压应力值较大，在7月份时达到最大值，坝中最大主压应力为1.00 MPa。

（2）低温月份时：上游面的坝肩拉应力较大，在1、2月份时达到最大值，坝肩最大主拉应力为1.00 MPa；上游面的压应力值较小；下游面的坝肩、坝中均出现不同程度的拉应力，在1月份时分别为0.73，0.58 MPa；下游面的压应力值亦较小。

（3）由计算结果可知，低温时拱坝以拉应力为主，上游面的坝肩处拉应力值较大。高温时，拱坝以压应力为主，但在上游坝中区域也会出现较大的拉应力值。

3.4 确定性模型结果

根据坝工理论和弹性理论，水压力产生的坝体应力可用水头的多项式表示，而变温引起的温度应力可用周期项表示。因此，上述有限元计算结果拟定模型如下：

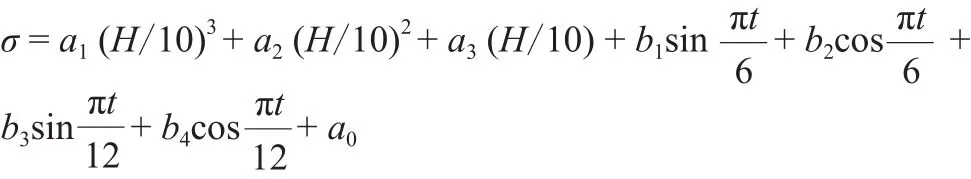
式中：σ为水压、温度荷载作用下坝体典型区域主应力值，MPa；a 、b为回归系数；H为坝前水位高程，m；t为月份。坝体典型区域主应力值所对应的回归系数见表3。

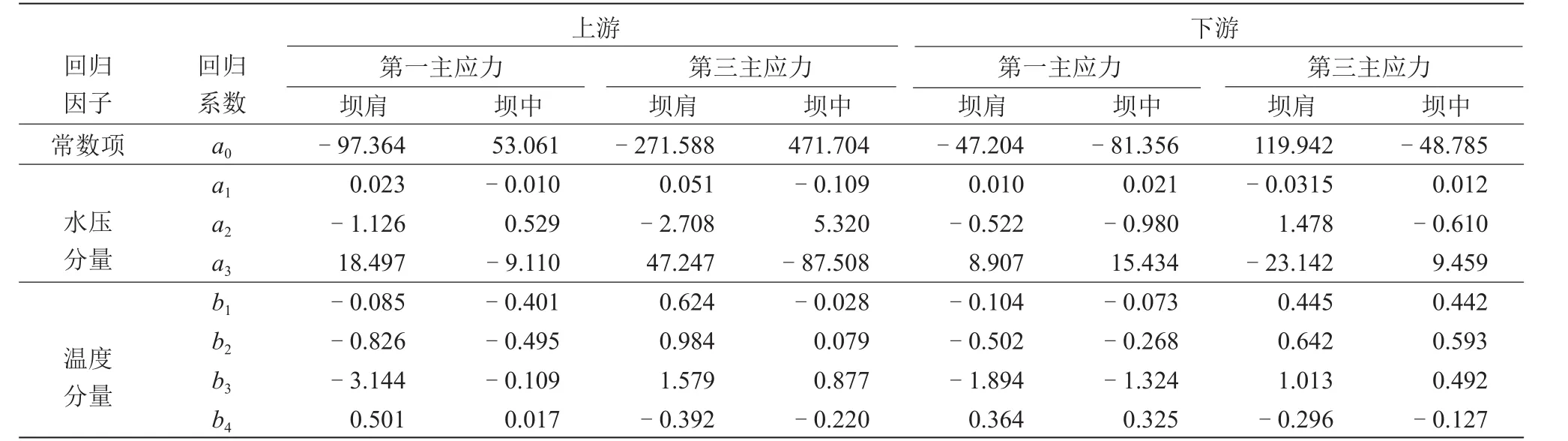
表3 坝体典型区域主应力值所对应的回归系数表

4 实际坝体裂缝情况分析

里石门拱坝运行多年，坝体在不同荷载作用下出现了多处裂缝，下游坝面裂缝示意见图12，相应检测成果见表4。

图12 下游坝面裂缝示意图

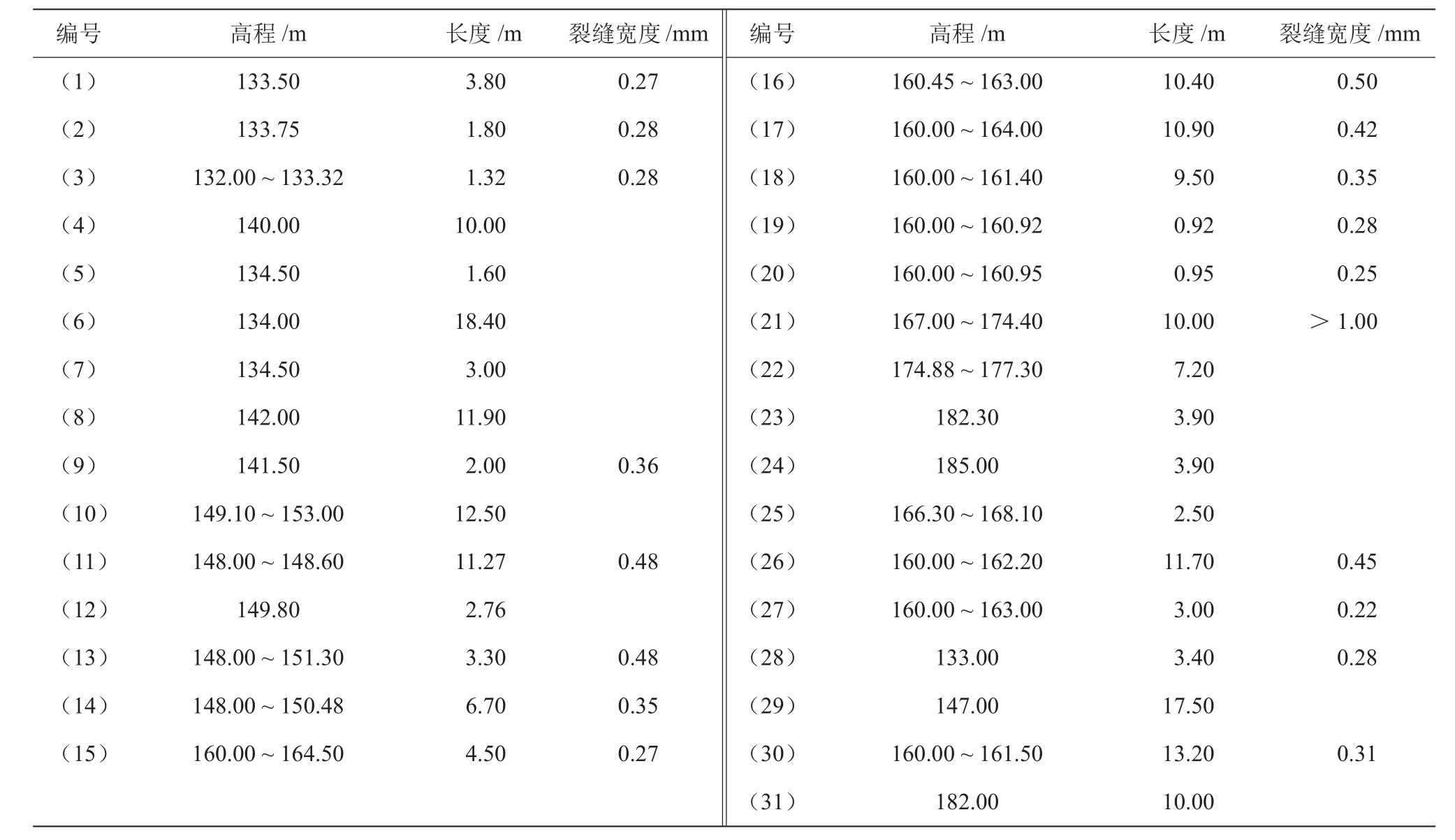
表4 大坝下游面裂缝检测成果表

根据确定性模型成果及图12、表4可知：

（1）下游面裂缝多集中在坝中及坝肩区域，其中有多处超过10 m的贯穿性裂缝，如坝中裂缝编号（4）、（6）、（8）、（10）、（11），坝肩裂缝编号（21）、（30）、（31）。

（2）由有限元计算结果可知：坝体下游面在高水位下，坝中主拉应力较大，低水位下，坝肩主拉应力较大；坝体下游面在低温时以拉应力为主，高温时，以压应力为主。里石门拱坝运行过年，经历了多种不利运行工况，也易在坝中及坝肩处出现裂缝。

（3）由图5可知，坝体下游面在坝中及坝肩区域出现较多拉应力区，与图12中实际裂缝发生区域基本吻合。也一定程度说明了确定性模型的可靠性。

5 主要结论

本文基于反演后的坝体弹模参数，得到里石门拱坝应力的确定性模型。并获得以下结论：

（1）在里石门大坝应力监测资料失准的情况下，本文提供了一种可供参考的确定性模型。大坝的弹性模量依据水平位移统计模型分离出的水压分量位移，可靠度高。

（2）坝体应力和变形计算结果基本上合理，符合有限元方法计算的一般规律，且水压、温度分量下的计算位移与监控数据统计模型分离出的位移数值基本一致，可作为应力计算准确度的评判依据，认为有限元分析成果基本可靠。

（3）低水位时，坝体整体位移、应力值较小。高水位时，坝顶的径向、切向位移逐渐增大。应力方面，上游面主拉应力值整体较小，主压应力值也均在混凝土容许压应力以下；下游面坝中处主拉应力相对较大。符合拱坝水压荷载下应力变形一般规律。

（4）高温月份时，坝体整体位移倾向上游。上游面坝中的拉应力较大，这也是里石门拱坝空库高温工况下出现裂缝的原因之一；下游面的拉应力值较小，坝中的压应力值较大。低温月份时，坝体整体位移倾向下游。上游面的坝肩处拉应力较大，压应力值较小；下游面的主拉、主压应力均较小。

（5）里石门大坝实际的裂缝分布区域与有限元计算的高拉应力区基本一致，也一定程度说明了确定性模型的可靠性。

[1] 蒋存仁.混凝土重力坝变形监测资料分析研究[D].兰州：兰州交通大学，2013.

[2] 刘成栋，向衍.碗窑水库碾压混凝土重力坝物理力学参数反演分析[J].中国农村水利水电，2009(9)：115 - 117.

[3] 王海娟.基于ANSYS的拱坝等效应力分析及考虑施工加载过程对坝体应力的影响研究[D].西安：西北农林科技大学，2010.

[4] 李晓军，辛全才.基于ANSYS的高拱坝三维有限元分析[J].中国农村水利水电，2008(1)：91 - 94.

[5] 关文海.混凝土拱坝变形分析的安全监控模型研究与应用[D].西安：西安理工大学，2006.

[6] 王海青.碾压混凝土拱坝温度应力仿真分析[D].南京：河海大学，2006.