高中数学总复习与培养学生思维“五性”

广东省惠东县教育局教研室(516300) 汪辉

数学学习的过程是解题的过程,数学解题方法是数学思维的体现,数学思维是理性思维的重要载体.而解题教学是数学教学中培养学生数学思维的重要环节.学数学离不开解题.有人认为熟能生巧,只要多解题就行,其实熟能生巧是适用于技艺型的.数学学习属于探索型学习,更重要的应是思维训练和品质塑造.教师要把精力放在优选习题,充分挖掘例习题训练思维的内在潜力与充分发挥例习题的教育功能上,让解题教学更重创新、重分析、重规律、重引申、重发展.对培养学生思维的“五性”有着重要作用.下面就结合高三数学第二轮复习教学,谈谈具体认识和做法.

一、变更命题的表达形式,培养学生思维的深刻性.

例 (1)已知函数f(x)=lg(ax-bx)(常数a＞1＞b＞0),求证:函数f(x)的图像上任意两点的所连成直线都不平行于x轴.

(2)已知函数f(x)=lg(ax-bx)(常数a＞1＞b＞0),求证:函数f(x)=0至多只有一个实数解.

(3)已知函数f(x)=lg(ax-bx)(常数a＞1＞b＞0),求证:函数f(x)在定义域内是增函数.

同一问题,变更命题的表达形式,可以从不同角度提出来,多题一解,使解题回规通性通法,使思维程度不断得到升化.加强这方面的训练,培养了学生审题习惯,从而达到使学生养成深刻理解问题本质的能力.

二、寻求不同解题途径与思维方式,培养学生思维的广阔性.

例 给定抛物线C:y2=4x,F是C的焦点,过点F直线L与C相交于A、B两点.(1)设L的斜率为1,求OA与OB夹角的大小;(2)略.

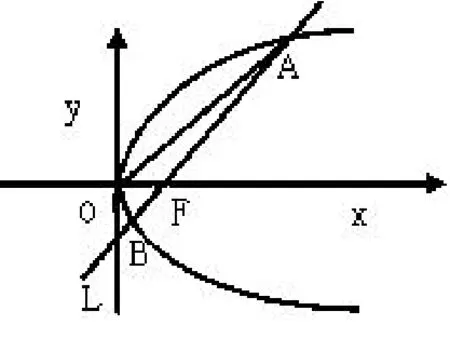
图1

看问题由已知得出直线L的方程为y=x-1与抛物线y2=4x联立后,设A(x1,y1),B(x2,y2),可得

○1设 ∠xOA=α,∠xOB=β,求tan(α+β)即为∠AOB的正切值.○

上述第一种解法,引出学生对两角和公式的复习,直线的倾斜角和直线与直线夹角的联系与区别,倾斜角与斜率的关系;第二种解法引出学生辨别直线“夹角公式”和“有向角”公式的区别和联系,直线夹角与斜率的关系;第三种解法简洁,引出平面向量数量积,解析几何基本思想和方法.凸显向量这一工具知识点在解决初等数学问题的优越性.对问题解答的思维方式不同,产生解题方法各异,这样训练有益于打破思维定势,开拓学生思路,优化解题方法,从而培养学生发散思维能力.

成品油市场作为中国能源行业的重要组成部分，对国民经济的平稳运行有着重要影响。合理的定价机制、公平的市场环境、完善的制度建设是成品油市场高效有序运行的重要保障。

三、变换几何图形的位置、形状和大小,培养学生思维的灵活性.

例 正三棱柱ABCA1B1C1中,各棱长均为 2,M为AA1的中点,N为BC的中点,则在棱柱的表面上从点M到点N的最短距离是多少?并求之.

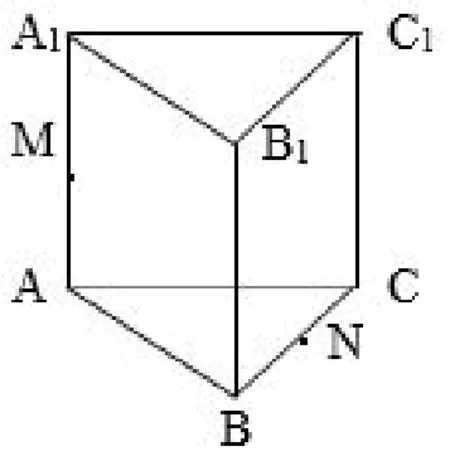
图2

分析 从点M到N有几种情况:

(1)沿侧面经CC1到N,或沿侧面经BB1到N.由正三梭柱可知,最短距离相等.

(2)沿底面经AB到达点N或经过AC到达N,这两种情况最短距离也相等.

这样只要计算(1)、(2)的一种情况,结果比较后即可确定最短距离.

例 已知长方体ABCDA1B1C1D1中:

(1)若AB=5,AA1=4,AD=3,试求在长方体表面上从A到C1的最短路线.

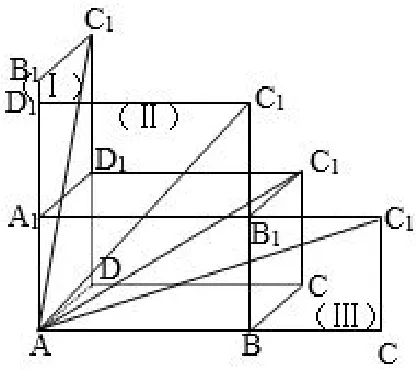
图3

分析 (1)沿表面经过A1B1(或CD)到C1点;

(2)沿表面BB1(或DD1)到C;

(3)沿表面经A1D1(或BC)到C1.

将有关平面折直,构成如右图(I)、(II)、(III)三平面.由平面几何知识,六条线路可归结为此三种情况,最短距离必在平面 (I)、(II)、(III)中.

这样引导学生把例习题多层次变换,既加强了知识之间联系,又激发学生学习兴趣,达到既巩固知识又培养能力的目的,同时强化了学生解题思维的敏捷性.

四、改变题目的条件和结论,培养学生思维的批判性.

例 (1)已知方程x2+(m-2)x+5+m=0的两个根一个大于1,而另一个根小于1,求实数m的取值范围.

(2)已知方程x2+(m-2)x+5+m=0的两个根都在区间(1,2)内,求实数m的取值范围.

(3)已知方程x2+(m-2)x+5+m=0的两个根分别在区间(0,1)和(1,2)内,求实数m的取值范围.

如此一题多变,会使学生对一元二次方程根的分布情况有一个清晰的认识,同时对韦达定理、二次函数的图像更加理解,使知识系统化.(解略).这样的训练可以克服学生静止、孤立地看问题的习惯,促进学生对数学思想方法的再认识,培养学生研究、探索问题的能力以及对数学问题的批判价值观.

五、变封闭式题目为开放型题目,培养学生的思维创造性.

例 填空题.已知α、β是两个不同的平面,m、n是平面α及β之外的两条直线,由α⊥β,n⊥β,m⊥α,可得m⊥n.

若将此题改为已知α、β是两个不同的平面,m、n平面α及β之外的两条直线.给出四个论断:○1m⊥n、○2α⊥β、○3n⊥β、○4m⊥α.以其中三个论断为条件,余下一个论断作为结论,写出你认为正确的一个命题.(1999年全国高考题)

总之,高考离不开解题,要想在竞争激烈的高考中取得胜利,就必须对学生进行上述解题的“拔高”训练(尤其是备考的第二阶段),即培养学生思维的“五性”,这也是提高高中数学复习效率行之有效的方法.