一种带有阻尼板航行体的弹道模型与计算

任佰足， 边晓阳

(1. 海军92330部队装备部， 山东 青岛 266102；2. 海军航空工程学院 研究生管理大队， 山东 烟台 264001)

带有阻尼板的水下发射航行体， 由于功能设定的要求， 自身不具备持续的动力推动装置， 其采用“冷发射”的发射方法发射后需要回收重复利用. 航行体从发射筒中被弹射出去后， 阻尼板迅速展开， 改变了航行体原本垂直向上的运动轨迹， 使其沿着发射载体的侧向进行偏移运动， 从而使航行体在出水再回落水后的过程中可以保证弹道不触碰发射载体[1]. 构建一个关于带有阻尼板航行体的水中上升、 出水、 空中飞行、 入水以及水中下沉阶段的弹道数学模型是研究的基础(见图 1).

目前对水下发射航行体的弹道模拟研究主要集中于水中上升弹道、 出水弹道以及入水弹道等领域. 例如姚保太等[2]采用MSC.DYTRAN有限元分析软件建立起航行体水弹道仿真计算模型， 并对一种航行体复杂的水弹道特性进行分析； 李杰等[3]研究了附着空泡对潜射导弹弹道的影响， 建立了肩空泡尾段横向力模型， 并将仿真得到的水弹道结果与同工况的试验结果进行比较， 验证了建立的空泡尾段横向力模型能够反映空泡对潜射导弹局部流体动力的影响规律； 袁绪龙等[4]建立了无动力潜射导弹运载器出水弹道数学模型并进行仿真， 仿真结果与实测数据吻合良好； 田宝国等[5]主要针对波浪作用下的无动力运载器进行了弹道轨迹仿真. 本文针对该类型航行体出水之后在重力作用下回落入水的弹道变化特性， 建立了一个完整的弹道数学模型.

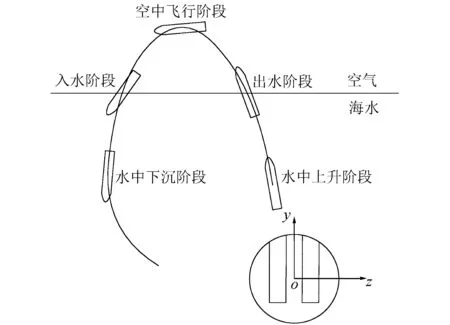
图 1 带有阻尼板的航行体弹道轨迹示意图Fig.1 Diagram of vehicle trajectory with damping plate

1 坐标系的选取及运动参数的定义

1.1 坐标系的选取

本文用到的坐标系有发射坐标系和航行体坐标系， 如图 2 所示.

发射坐标系坐标原点o位于航行体脱离发射筒时质心对应的水面位置，x轴与发射瞬时发射载体的航行方向一致，y轴沿过坐标原点的铅垂线， 指向天空，z轴由右手法则确定[6].

图 2 发射坐标系与航行体坐标系示意图Fig.2 Diagram of launch coordinate system and vehicle coordinate system

航行体坐标系坐标原点o0位于航行体质心所在横截面与航行体纵轴的交点，x0轴沿航行体纵轴， 指向弹头为正，y0轴在航行体纵对称面内， 与x0轴垂直，z0轴由右手法则确定.

1.2 运动参数的定义

水下发射航行体具有6个自由度， 航行体坐标系相对于发射坐标系的位置就由6个坐标来确定： 航行体坐标系坐标原点在发射坐标系中的3个坐标x，y，z和航行体坐标系与发射坐标系之间的3个欧拉角θ，ψ和γ[7-8]. 其中：x表示水平位移， 为航行体质心对应在ox轴上的位移；y表示航行深度， 为航行体质心对应在oy轴上的位移；z表示侧向位移， 为航行体质心对应在oz轴上的位移；θ为俯仰角， 为航行体纵轴o0x0与水平面(oxz平面)的夹角， 以航行体头部向上为正；ψ为偏航角， 为航行体纵轴o0x0在水平面的投影与发射坐标系ox轴的夹角， 从航行体尾部向前看时弹轴偏向参考航向o0x0的左侧为正；γ为滚转角， 为航行体立轴o0y0与通过纵轴o0x0的铅锤平面间的夹角， 从航行体尾部向前看时顺时针滚动为正.

以上所有方向均遵循右手螺旋规则.

2 航行体受力分析及运动方程组

2.1 航行体受力分析

航行体从水下发射后经历水中上升段、 出水段、 空中飞行段、 入水段和水中下沉段5个阶段， 共受到流体动力[9]、 重力、 浮力以及阻尼板阻力等力的作用， 其中流体动力按照流体介质将其分解为理想流体动力和粘性流体动力， 具体的力学分析如下：

1) 航行体阻力[10]

(1)

2) 航行体尾部压力

航行体被高压燃气推出发射筒后， 燃气在航行体尾部形成尾部燃气泡， 尾部燃气泡附着在航行体尾部并逐渐衰减下去， 直至航行体尾部出水， 尾部燃气泡才会彻底溃灭消失.

(2)

在具体计算时需提供出筒时的底部初始压力Pb0， 然后利用以下公式来近似计算尾部燃气泡中的压强

Pb(t)=Pb0·fb(τ).

(3)

尾部燃气泡压强再乘以尾截面的面积就可得到航行体尾部压力， 即

Fx2=PB·SB,

(4)

式中： PB为尾部压强； SB为尾段截面积. 尾部压强除水中段外其余阶段均为零.

3) 净浮力及净浮力矩

由于重力原因航行体受到浮力和浮力矩， 而浮力在数值上等于航行体所排开的水受到的重力为

B=ρgV,

(5)

式中： ρ为海水密度； V为航行体排开水的体积. 浮力方向铅垂向上， 而浮力矩的方向与物体姿态有关， 对于全湿情况， 浮力和航行体水平放置时的浮力可以按照下式求得

(6)

式中： 积分上限xA为航行体头部的x坐标； 下限xT为航行体尾部的x坐标， 若航行体已经开始出水， 则xA为弹轴与水面交点的x坐标； d(x)为沿x轴处的航行体直径； (xc,yc,zc)为航行体浮心在航行体坐标系中的坐标[11].

净浮力是指作用在航行体上的浮力与重力之和， 由于航行体坐标系选在质心， 所以重力产生的力矩为零， 浮力矩即为净浮力矩， 具体表达式如下

(7)

(8)

4) 横向力

使用Morison公式计算航行体受到的横向力.Morison公式是求解波浪力的基本公式. 假定一圆柱体垂直固定在流体之中， 波浪沿x轴方向流动. 单位长度圆柱体上沿x轴方向的波浪力为[12]

F(x,z,t)=FI(x,z,t)+FD(x,z,t).

(9)

波浪对单位长度圆柱体上的总惯性力FI为

(10)

Morison公式中的阻力FD项， 是受流体的粘性效应影响而产生的， 一般默认阻力和流体质点速度的平方呈正比关系. 根据细长体理论， 航行体在水中运动所受横向力由Morison公式求得

(11)

式中： ρ为流体介质的密度； Cd为粘性系数； Vy0和Vz0为航行体在航行体坐标系中的速度分量.

5) 阻尼板阻力及阻尼力矩

在计算阻尼板的受力情况时， 首先将每一块阻尼板的受力按照平板进行计算， 然后将所有阻尼板的受力与力矩相加得到阻尼板对航行体的整体作用力和作用力矩.

对于无界流场中的平板(如图 3 所示)， 其受力情况可以由下面的公式计算得到

(12)

式中： v∞为来流速度； Cd为平板阻力系数； S为平板面积.

考虑壁面附近的平板受力， 认为这时的绕流运动对平板和壁面会产生相同大小的作用力， 力的方向分别垂直于平板表面和壁面. 二者的合力经过角点(见图 4)， 合力大小为

(13)

图 3 平板受力示意图Fig.3 Diagram of tablet force

图 4 有壁面存在时的平板受力示意图Fig.4 Diagram of tablet force with wall

由此可以得出单个阻尼板产生的力为

(14)

对航行体产生的合力和合力矩为

(15)

(16)

式中： nb为阻尼板个数； Sb0为阻尼板面积； α为阻尼板展开角度； Cd为平板阻力系数； xT为弹尾x坐标； R为航行体最大半径； xbi, ybi, zbi为舵板阻力作用点.

2.2 航行体附加质量计算

航行体为细长体， 且形状接近轴对称. 考虑到对称性， 因此附加质量矩阵A中仅A11(x),A22(x),A33(x),A55(x),A66(x),A26(x)和A35(x)为非零项. 采用细长体理论， 即假定航行体各截面之间没有干扰， 航行体的附加质量是截面附加质量沿航行体纵轴x方向的积分. 在穿越水面阶段， 则仅计算仍在水下的航行体部分的附加质量， 全湿情况的附加质量的计算如下所示

(17)

A11与航行体质量相比很小， 但在航行体出水过程中， 它的变化率并不小， 并产生了正的轴向力， 致使航行体在轴向有所加速， 所以针对该航行体的弹道特殊性，A11在计算中不应忽略， 其近似计算公式如下

(18)

式中：μx和μy为修正系数.

综上， 带有阻尼板的航行体受到总的外力及外力矩为

(19)

2.3 航行体运动学方程

(20)

(21)

2.4 航行体动力学方程

根据动量定理和动量矩定理， 航行体的动力学方程为[14-15]

(22)

(23)

式中：G为航行体和周围流体的总动量；H为相对于航行体坐标系原点o0的总动量矩；ω为航行体的角速度矢量；V为航行体的平移速度矢量；F和M分别为航行体所受的外力和外力矩；G和H可以用系统的惯性张量和速度矢量的点积表示出来， 即

(24)

式中：U=(vx0,vy0,vz0,ωx0,ωy0,ωz0)T为六维速度矢量的转置列矢量；A=[Aij]6×6为附加流体质量系数矩阵；M=[Mij]6×6为航行体惯性系数矩阵， 其表达式为

(25)

式中：m为航行体质量；Jij(i,j=1,2,3)为航行体转动惯量； (xc,yc,zc)为质心坐标. 综上可以得到G和H的分量表达式为

(26)

由此， 得到如下分量形式的运动微分方程组

(27)

以上方程组可整理成如下矩阵形式

(28)

其中：

(29)

(30)

将计算得到的外力、 外力矩和附加质量代入式(28)， 并对此微分方程组数值求解， 得到随时间变化的速度和角速度.

3 弹道模型的简化假设

3.1 空泡的影响及简化处理

水下航行体高速运行时， 会在肩部出现压力最小点， 当该压力足够小时， 流体中的气核开始膨胀， 最后连成一片附着在航行体表面， 该空泡属于固定空泡[16]. 通过液体掺混与随后从空化区尾端回冲等过程， 固定空泡可能发育成长， 然后溃灭， 出现周期性循环， 但从准恒定的角度来看其是动态稳定的. 由于空泡内的压力很小， 计算浮力和附加质量时要扣除空泡覆盖面上的压力积分， 现使用经验公式得出空泡相对长度

(31)

用积分计算附加质量时， 有空泡覆盖的一段不计算在内. 在计算全湿情况附加质量的公式基础上， 计算带空泡的附加质量积分变为

(32)

式中：aij为计算附加质量Aij的积分函数；xs和xe分别为空泡距头部的起始位置坐标和结束位置坐标.

浮力的计算也是同样的方法， 在全湿情况计算浮力的基础上， 带空泡情况下计算浮力的积分公式中有空泡的一段不计算在内.

3.2 弹道模型的基本假设

对带有阻尼板的航行体弹道进行精确的模拟十分复杂， 尤其是出水和入水两个过程本身具有着不确定性和随机性， 本文在这两个弹道过程的模型构建中进行了一定的简化假设：

1) 出水弹道模型的基本假设

航行体出水时， 在头部接近自由液面时， 液面会隆起， 所以即使头部已经高出了水平面， 头部可能还未出水. 同样， 在航行体出水的整个过程中， 都会有隆起的水附着在航行体表面. 在这里近似认为头部高出水平面的部分就是已出水的部分.

当航行体头部出水时， 肩空泡会不断地随着流场的改变而发生变化， 而当肩部出水后， 肩空泡会逐渐溃灭. 由于头部出水的时间很短， 空泡的溃灭会在一瞬间完成， 在这里假设头部一出水， 空泡就消失. 尾部燃气泡的溃灭也有类似的假设.

2) 入水弹道模型的基本假设

航行体入水迅速冲击水面， 经历一个砰击的过程， 使航行体遭受很大的砰击力. 航行体头部冲击水面时间很短， 几乎在瞬间完成. 在这里利用近似的估算方法求出冲击后航行体的速度. 冲击之前航行体的速度为V0， 冲击之后航行体的速度为Vt， 将航行体假设为一块半径为Rr的圆盘， 半径尺寸相当于头部入水后航行体与水面相交的圆的半径， 当航行体的倾斜角度θ不同时

(33)

冲击后航行体的速度为

(34)

4 仿真与试验对比分析

为了验证弹道模型的可行性和合理性， 以三发次的实弹弹道数据作为参照标准对仿真弹道进行数据的对比分析. 由于实弹发射时的出筒速度为一随机值， 所以根据采集到的出筒速度数据作为仿真前提， 利用MATLAB仿真平台对该航行体进行弹道仿真[17-18]， 得到了弹道轨迹与弹道特征点数据. 将仿真数据与三发实测弹道特征点数据进行对比， 考虑到弹道试验工况的复杂性， 仿真数据与试验数据吻合情况较好， 具体的仿真情况如图 5～图 7 所示， 数据对比如表 1 所示.

图 5 质心x坐标仿真曲线Fig.5 Simulation curve of centroid x-coordinate

图 6 质心y坐标仿真曲线Fig.6 Simulation curve of centroid y-coordinate

图 7 质心z坐标仿真曲线Fig.7 Simulation curve of centroid z-coordinate

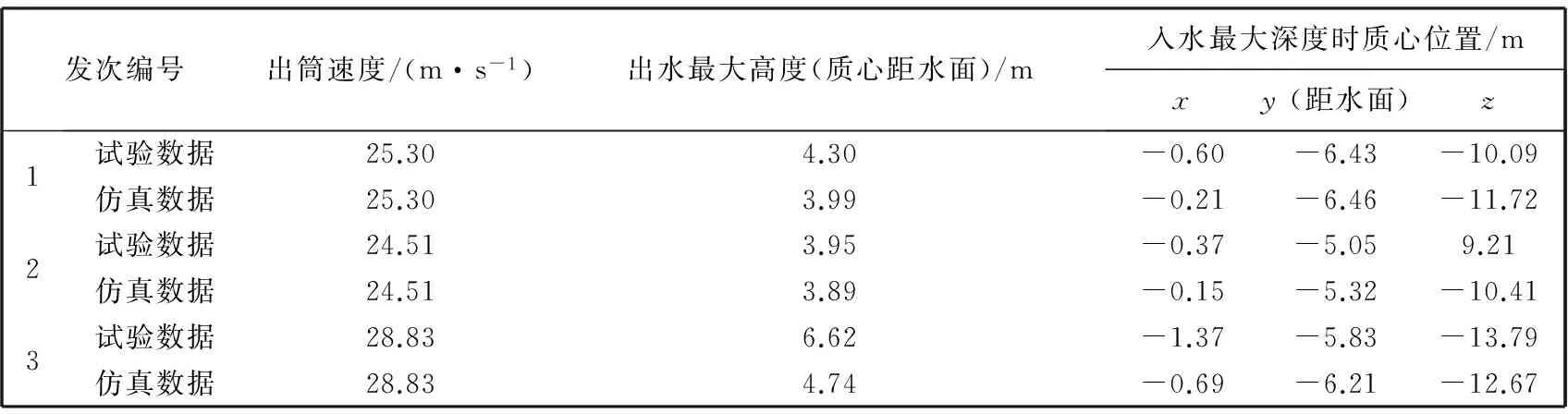
发次编号出筒速度/(m·s-1)出水最大高度(质心距水面)/m入水最大深度时质心位置/mxy(距水面)z1试验数据25.304.30-0.60-6.43-10.09仿真数据25.303.99-0.21-6.46-11.722试验数据24.513.95-0.37-5.059.21仿真数据24.513.89-0.15-5.32-10.413试验数据28.836.62-1.37-5.83-13.79仿真数据28.834.74-0.69-6.21-12.67

5 结 论

本文针对带有阻尼板的航行体水下发射出水后， 在重力作用下重新入水的弹道特性， 建立了完备的弹道数学模型. 通过对具体的算例进行仿真， 仿真结果可以直观地描述出航行体质心在3个分轴随时间的变化趋势， 以及航行体姿态角随时间的变化趋势.

将仿真弹道的特征点数据与三发次实测弹道特征点数据进行对比， 吻合情况较好， 验证了所构建的该航行体弹道数学模型的合理性和可行性. 今后可以根据实际需求在此模型基础上对航行体弹道轨迹进行各方面的研究.

[1]李四超. 水下航行体舵板张开特性研究与分析[J]. 海军航空工程学院学报， 2016， 31(4)： 475-479. Li Sichao. Research and analysis for opening property of the rudder on underwater vehicle[J]. Journal of Naval Aeronautical and Astronautical University， 2016， 31(4)： 475-479. (in Chinese)

[2]姚保太， 都军民. 一种航行体水弹道的数值仿真与试验研究[J]. 舰船科学技术， 2015， 37(7)： 104-107. Yao Baotai， Du Junmin. Numerical simulation and experimental study on a water trajectory of vehicle[J]. Ship Science and Technology， 2015， 37(7)： 104-107. (in Chinese)

[3]李杰， 鲁传敬， 陈鑫. 附着空泡对潜射导弹弹道影响分析[J]. 弹道学报， 2014， 26(3)： 54-58. Li Jie， Lu Chuanjing， Chen Xin. Analysis on influence of attached cavity on the trajectory of submarine launched missile[J]. Journal of Ballistics， 2014， 26 (3)： 54-58. (in Chinese)

[4]袁绪龙， 张宇文， 殷崇一. 无动力潜射导弹运载器出水弹道建模与实验验证[J]. 弹箭与制导学报， 2003, (S5)： 187-189. Yuan Xulong， Zhang Yuwen， Yin Chongyi. Water trajectory modeling and experimental verification of non-powered submarine launched missile carrier[J]. Journal of Rockets and Guidance， 2003, (S5)： 187-189. (in Chinese)

[5]田宝国， 耿霆. 波浪力作用下无动力运载器水弹道仿真[J]. 计算机与数字工程， 2011， 39 (1)： 7-9. Tian Baoguo， Geng Ting. Water trajectory simulation of non-powered vehicle under wave force[J]. Computer and Digital Engineering， 2011， 39(1)： 7-9. (in Chinese)

[6]周源， 齐强， 陈志刚. 潜射导弹水中弹道建模与仿真[J]. 四川兵工学报， 2012， 33(9)： 16-18. Zhou Yuan， Qi Qiang， Chen Zhigang. Modeling and simulation submarine launched missile water trajectory[J]. Journal of Sichuan Ordnance, 2012， 33(9)： 16-18. (in Chinese)

[7]齐强， 陈志刚， 周源. 航行器水中运动数学模型及数值仿真[J]. 舰船科学技术， 2014， 36(5)： 80-83. Qi Qiang， Chen Zhigang, Zhou Yuan. Mathematical model and numerical simulation of water movement in aircraft[J]. Ship Science and Technology， 2014， 36(5)： 80-83. (in Chinese)

[8]刘曜， 马震宇. 导弹水下垂直发射的弹道研究[J]. 战术导弹技术， 2006, (2)： 21-25. Liu Yan， Ma Zhenyu. Research on trajectory and hot separation of vertical underwater launched missile[J]. Tactical Missile Technology， 2006, (2)： 21-25. (in Chinese)

[9]黄景泉. 鱼雷流体力学[M]. 西安： 西北工业大学出版社， 1989.

[10]欧阳国军. 水下发射导弹运载器的弹道与控制研究[D]. 烟台： 海军航空工程学院， 1990.

[11]Ye H J， Zhou H， Wang X Y. Modeling and simulation on the underwater trajectory of non-powered vehicle discharged from the broadside[J]. Journal of Harbin Institude of Technology， 2016， 23 (2)： 79-86.

[12]张重先. 波浪扰动下的小型潜射导弹出水动力学建模与仿真[J]. 国防科学大学学报， 2015， 37(6)： 91-95. Zhang Chongxian. Dynamics modeling and simulation of water-exit course of small submarine-launched missile under wave disturbance[J]. Journal of National University of Defense Technology， 2015， 37(6)： 91-95. (in Chinese)

[13]方宁， 宋召青. 潜载垂直发射导弹水下弹道建模与仿真[J]. 海军航空工程学院学报， 2010， 25(3)： 311-314. Fang Ning， Song Zhaoqing. Modeling and simulation for the underwater trajectory of submarine-based verticallaunched missile[J]. Journal of Naval Aeronautical and Astronautical University， 2010， 25(3)： 311-314. (in Chinese)

[14]严卫生. 鱼雷航行力学[M]. 西安： 西北工业大学出版社， 2005.

[15]葛晖. 潜射导弹发射安全性研究[D]. 西安： 西北工业大学， 2004.

[16]丁晖. 空化与空蚀的影响因素及其研究方法分析[J]. 黑龙江水专学报， 2005， 32(4)： 66-67. Ding Hui. Analysis on studying method and influence factor of hollow corruption and hollow erosion[J]. Journal of Engineering of Heilongjiang， 2005， 32(4)： 66-67. (in Chinese)

[17]宋海龙. 水弹道建模与仿真方法研究[D]. 哈尔滨： 哈尔滨工业大学学报， 2014.

[18]薛定宇， 陈阳泉. 高等应用数学问题的Matlab求解[M]. 北京： 清华大学出版社， 2004.