考虑流固耦合的双弯头压裂管汇的振动特性

祝效华 曾云义 陈 波 陶浩然

1.西南石油大学机电工程学院 2.中国石化广元天然气净化有限公司

3.中国石化中原油田井下特种作业公司 4. 中国石油西南油气田公司物资分公司

在页岩气开采过程中，通常需要借助大型体积压裂实现高效开采[1]。在压裂作业过程中，压裂车泵出的压裂液不均匀，在弯头处压裂液会对管壁产生随时间变化的激振力，引起压裂管汇产生耦合振动[2]。现场调研也反馈波动流和弯管导致的振动是引起压裂管件疲劳破坏与源动力机械损坏的主要原因之一。针对管汇的振动问题，Païdoussis等[3-4]建立了描述输流管道非线性动力学行为的流固耦合振动模型，并分析了脉动流体对管道振动特性的影响规律；Ghayesh等[5]分析了弹性支撑对管道非线性振动特性的影响；Ghazali[6]讨论了压力变化对管汇振动的影响，并提出了几种管线状态监测技术；王琳等[7]用广义积分法建立了输流曲管动力学方程组，并计算了几种典型边界条件下的固有频率及曲管失稳的临界流速。以往分析基本针对于低压情况下管汇的振动规律，计算结论不再适用于压裂现场高压或超高压压裂管汇的振动情况。为了减小管汇的振动、减少因振动诱发的工程事故，有必要开展弯头在高压条件下的振动分析研究。笔者推导了高压弯管在各平面内的运动方程，编程计算了弯管振动强度随各个参数变化的曲线。建立了弯管的单向流固耦合数值模型，通过现场实测数据验证了数值模型的有效性，使用该模型计算了结构参数对双弯头弯管固有频率的影响，为现场管汇的合理布局提供理论依据。

1 输流弯管运动方程的推导

弯头是连接两条轴线不重合的直管段的管元件。压裂液流经弯头其流动方向发生变化，使脉动流的轴向惯性作用转变成为压裂液与内管壁的径向耦合，从而产生振动。当压裂液经过如图1所示的双弯头时，振动强度远大于单弯头。因此，弯管处压裂管线的振动除了来自于外部集中载荷作用，还要考虑流体与管线的流固耦合作用。

图1 高压压裂现场双弯头布局图

对弯管进行受力分析，采用微元法选取长为dl的微元段进行分析。令与弯管中心线相切的方向为z方向，垂直于弯管中心线所在平面为x方向，根据右手定则可以确定y方向的位置，三维直角坐标系与微元段所受到的力如图2所示。假设计算模型为均质、各向同性的等截面弯管，流体也为均质的单一流体。忽略流体的内摩擦与流体与管壁的摩擦作用。流固耦合对地面管汇产生的扭转作用非常小，扭转振动基本可以忽略不计。因此暂不考虑弯管的扭转。

图2 弯管微元计算模型图

对图2中弯管微元段在轴向上进行受力平衡分析，根据牛顿第二定律得到弯管的受力平衡方程为：

式中fx、fy、fz分别表示x、y、z方向上的作用力，N；ρS表示弯管材料的密度，kg/m³；AS表示弯管的横截面积，m2；w表示弯管在z方向上的运动位移，m；l表示弯管长度，m。

由于管单元趋于无穷小，即θ为无穷小量，此时存在：

将式（2）代入式（1）进行化简并忽略高阶无穷小量可以得到弯管在轴向上的受力平衡方程为：

根据牛顿第二定律可以得到管内流体的受力平衡方程：

式中p表示流体的压力，Pa；Af表示流体的横截面积，m2；ρf表示压裂液的密度，kg/m3；V表示流体的流动速度，m/s。

忽略高阶无穷小量并化简可以得到：

由圆弧弯管的弧长公式： 得到弯管的轴向应变为：

基于弹性力学理论得到弯管的物理方程为：

式中 表示弯管在z方向上的运动速度，m/s；h表示管壁的厚度，m； 表示流体流动的加速度，m/s2；μ表示弯管的泊松比；E表示弯管的弹性模量，Pa；R表示弯管轴线的半径，m。

由于弯头尺寸较大，管线长度较长，压裂管线中流体在经过弯头时流体的流动方向和形态被迫改变，流体压力的作用对弯头有“拉直”的效应，属于“Bourdon”耦合，因此在考虑弯管的Bourdon效应[8]后得到等内径弯管的连续方程为：

式中Kf表示由经典水及理论对流体状态方程的假设确定的流体体积模量，Pa。

式（3）、（5）、（7）、（8）即为弯管在轴向上的流固耦合振动方程。

计算弯管在yz平面上的流固耦合振动方程则有：

弯管的力矩平衡方程为：

受Bourdon耦合影响的弯管的连续方程[9]为：

式中 表示弯管绕x轴的转角速度，（°）/s；Y12表示弯管的压力增大系数；Y13表示弯管的弯曲因子；Mx表示x轴的扭矩，N·m。

由弯管轴向位移产生的转角的计算方程 为：

式中u、v分别表示管单元在x与y轴方向上的位移，m；Is与If分别表示弯管与流体截面的惯性矩，m4；G表示切变模量，分别表示弯管绕y、z轴的转角速度，（°）/s；My、Mz分别表示y、z轴的扭矩，N·m。

由弯曲管线的平面运动方程解得的u、v、w是与位移和时间有关的解析解，弯管运动解析式可近似表达为：

式中a表示弯管在两端固定时的最大振幅，m；b表示随着刚度的增大而减小常数值；ω表示弯管的振动频率，Hz。

通过求解运动方程即可求得弯管的振动频率与振动幅值。

由理论公式可以计算得到弯管在各个平面内的振动频率与振动幅值，但是在计算时认为各个平面内的振动互不影响，且不考虑其他因素的影响，因此计算结果与实际测量会存在一定误差。而随着各个平面方向上振动强度增大，对其他平面方向振动影响也越大，因此由理论公式计算得到的弯管的振动频率曲线与实际情况会存在一定误差，振动频率越高，相对误差也会略有增大。因此需要验证理论公式在压裂现场的适用性，通过将压裂管汇材料的物理参数与管内流体压力为60 MPa等施工参数代入式（9）、（10）、（11）、（12）对y、z平面内弯管的振动频率进行计算得到其振动频率约为8.63 Hz，将其与现场图3所示点测量数值进行对比可知管线振动频率误差最大约为17.02%。误差小于20%，在工程中尚可接受该误差，因此可以认为对压裂管振动计算的理论公式基本适用于指导压裂现场的振动计算。

压裂管汇的共振会严重影响压裂管件的使用寿命，为了防止管线共振，需要通过仿真方法计算压裂管线的固有频率从而在施工中使激振频率避开压裂管的固有频率。

2 双弯头弯管数值模型建立与仿真分析

2.1 模型及参数

为了验证仿真方法的可靠性，首先用设备状态综合分析系统与高频振动探头对中石油四川长宁天然气开发责任有限公司长宁1号H10-2压裂井随机抽取多根压裂管线的不同点对其垂直方向上的振动进行测量，测量点如图3所示。

通过对压裂车与交流管汇之间的管线进行长度尺寸的测量，利用三维软件建立了如图3-a所示压裂车与交流管汇之间的管线仿真计算模型。根据对现场实用压裂管切割制作标准件进行试验得到压裂管线密度为7 850 kg/m³，弹性模量（E）为209 GPa，泊松比为0.3，管线内径（d）为70 mm，直管壁厚（h1）为11 mm，弯管壁厚（h2）为19 mm。并在图2所建立的坐标系内对弯头在yz平面上的振动频率利用ANSYS Workbench软件进行分析计算，基于现场流速排量的计算，仿真计算时设置管内流速为压裂车出口处压力为60 MPa。选取弯头处的计算点与振动方向如图4中箭头所示，位置与方向与图3-b中的测量点的位置基本相同。

由于压裂管线抗拉刚度较大，其沿径向或轴向上变形量较小，但是在作业过程中压裂液与管壁摩擦产生的压降较大，因此在仿真过程中采用摩擦耦合的方式进行计算，并在此基础上以压裂车的振动频率作为管汇谐响应激振频率。

对图4所示模型中箭头所示点进行仿真计算，所得结果与高频振动探头测量图3-b所示振动测量点的振动频率与振动幅值进行对比，结果如图5所示。

由图5所示仿真计算结果与现场测量结果进行对比可看出，该点振动在10 Hz时弯管的振动幅值出现峰值约为0.505 63 mm，现场测量的该点的振动频率约10.4 Hz时出现振幅峰值为0.35 mm，振动幅值相差约为0.15 mm，这是由于压裂现场所使用的管道无法完全实现不同位置的材料均匀性与各向力学特性均保持不变，且压裂现场施工环境复杂，外界对管道振动存在较强的干扰以及在对管道振动强度进行现场测量的过程中误差等因素的存在，导致压裂现场测量所得谐响应频率与激振频率之间存在一定误差，但误差在可接受范围内，而由于仿真计算过程中不存在以上任何因素的干扰。因此计算所得谐响应频率与激振频率保持一致。由振动幅值的对比分析可以得知振动幅值可知，模型的计算振幅要略大于管道的测量振幅，且误差值约为22.1%。这是由于在压裂现场不存在完全固定，在对模型出入口两端施加固定约束与现场实际情况存在一定误差，可以认为误差在合理范围内。因此可以认为仿真计算方法可以用于计算管汇的固有频率与谐振频率。

图3 连接头处测量点与直管中间测量点照片

图4 仿真计算模型与计算点图

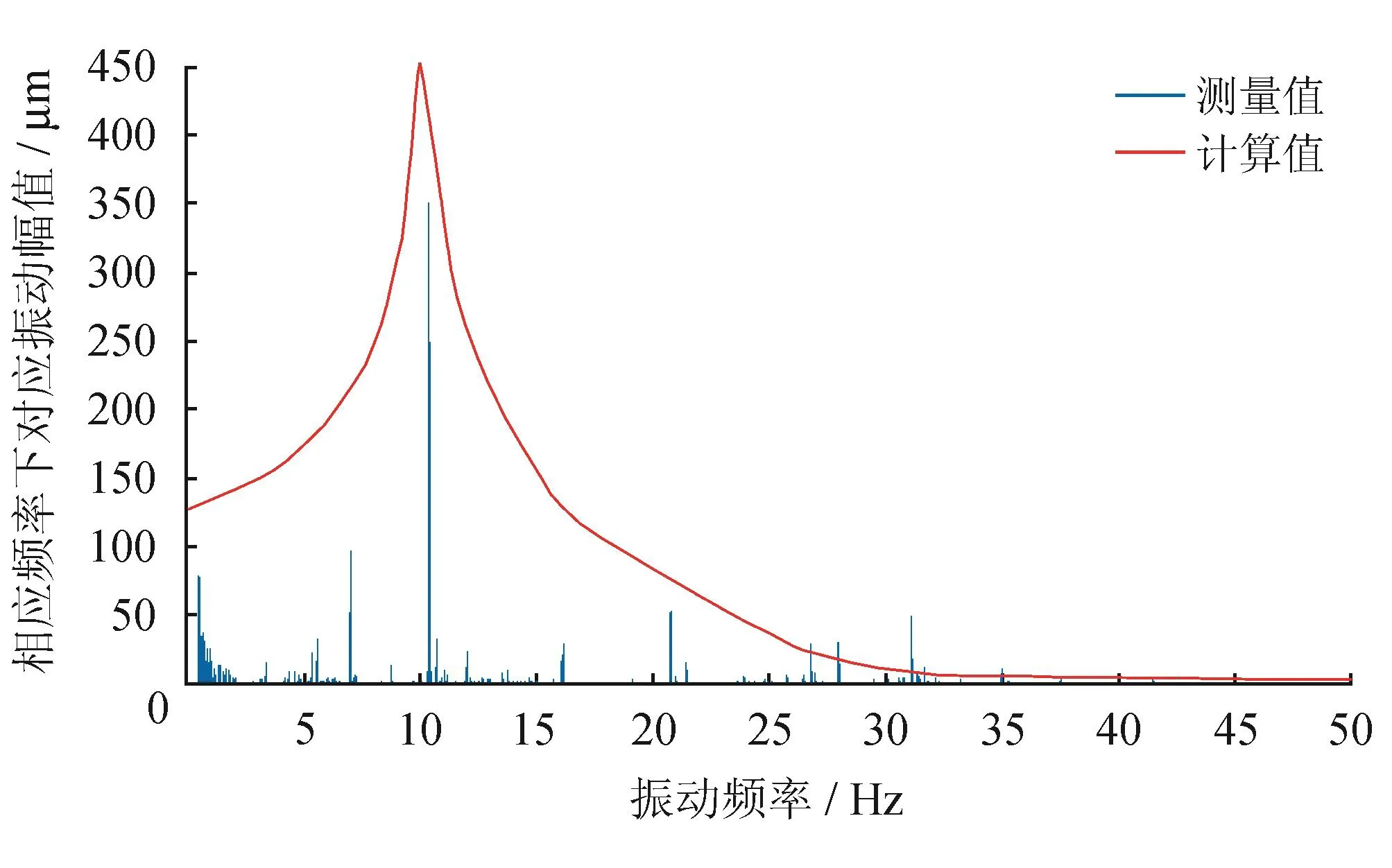
图5 仿真计算结果与测量结果对比图

为了减小仿真计算误差，使方程更加容易收敛，模型使用六面体划分网格，由于压裂液与管汇之间的作用状态可以认为是固液处于可分离状态、切向处于可滑动状态且只有一个接触面。因此采用Frictional固液表面非对称接触的接触类型[10]，进而得到如图6所示的带网格的双弯头弯管模型。

图6 双弯头弯管模型与网格图

如图6所示的压裂管在保持壁厚不变的情况下可生成多种管线内径。弯头相连的直管的长度为2 m，两条支管之间所成的角度即两个弯头的连接角度可变。然后对模型进行流体填充，划分网格，并对流体与管内壁接触的边界层的网格进行膨胀层处理。压裂管中采用水作为流体介质。整个分析中不考虑温度对流固耦合的影响。

2.2 数值分析方法

双弯头弯管流固耦合振动采用ANSYS Workbench—Fluent软件进行求解。在分析弯管模型流固耦合振动的模态时对模型的两端都约束6个方向的自由度，即添加固定约束。根据压裂现场实际情况，在模型左端流体的入口处将压裂液简化为正弦波动的连续流体，出口处的压力简化为60 MPa的常压，由于压裂弯管的抗拉刚度较大，在实际工作过程中压裂液对压裂管道的“拉直量”非常小。因此，在仿真计算过程中为了节约计算资源，忽略了管道的拉直效应，在双弯头处只考虑流固耦合不考虑弯头的Bourdon耦合效应，并对流体与压裂管的接触面添加相同的流固耦合标签。整个模型仿真过程的流固耦合通过此耦合面完成。由Fluent对流场进行分析，将计算得到的流场压力作为载荷直接添加到弯管的流固耦合面对压裂管的振动进行分析, 由于压裂管线的振动对流场中高压高速的流体影响较小，基本可以忽略不计。因此计算时为了能够节约计算资源采用单向流固耦合的算法[11]，整个分析过程经过若干次迭代后收敛。

在计算的过程中为了节约计算资源，可以适当增大单元格的大小，并减小计算的时间步长，但是为了使流固耦合计算容易收敛的单元格不能太大，因而在计算过程中要不断调整网格的大小，使其达到最合理的质量。因此计算采用分步式计算的方法来获取相对较短的计算时间[12]。

2.3 不同因素对固有频率的影响

2.3.1 流固耦合

为了分析流固耦合对管汇固有频率的影响，计算了双弯头内径为70 mm，连接角度为90°时空管与脉动流体流经双弯头弯管的前六阶固有频率，将其进行对比得到的计算结果如表1所示。

表1 双弯头的固有频率表 Hz

对表1进行分析对比可得知：在考虑模型的流固耦合作用时双弯管的固有频率比空管的固有频率明显降低。这是因为在当双弯管只对出入口进行固定支撑时由于管汇的支撑较少导致双弯管与管内流体耦合作用增强，从而对管汇因外力引起的振动响应计算产生较大的影响。因此在对双弯头弯管进行仿真计算时考虑流固耦合的作用是非常有必要的。

2.3.2 连接角度对双弯头弯管固有频率的影响

在流速与流体压力都相同的情况下，计算了内径为70 mm的双弯头的连接角度对双弯头弯管固有频率的影响。由于流体的脉动频率与外部的激振频率比较低，因此只提取前两阶模态进行分析，同时，为了对比计算双弯头弯管连接角度介于75°～105°的减振效果，采用了与模型验证相同的谐响应频率分析方法在弯管的入口处添加了一个激振频率，通过分析计算得到双弯头的连接角度与固有频率及谐响应振动幅值的关系，如图7所示。

图7 双弯头固有频率与振动幅值随连接角度变化图

由图7可看出，随着双弯头连接角度的不断增大，一阶固有频率呈现非线性递增的趋势，但增幅较小，可近似认为双弯头连接角度对一阶固有频率的变化影响不大；而二阶固有频率随着连接角度的增大出现先增大后减小的趋势，且在90°左右时出现最大值，即在压裂现场存在较低激振频率时，双弯头的连接角度控制在75°～105°的范围内时更不容易引起弯管的共振。

由图8可看出，弯管的谐响应振动幅值在90°附近时最低，将其与其他连接角度的振动幅值进行对比，将连接角度控制在90°附近时弯管的谐响应频率最大可减小约30%。

图8 双弯头固有频率随内径变化图

因此两个弯头的连接角度介于75°～105°时弯管振动有明显的减小，但由于一阶固有频率变化不大，若现场的激振频率较低时仍需要考虑管汇系统与外载激励的匹配以避免耦合共振[13]。

2.3.3 弯管内径对双弯头弯管固有频率的影响

在壁厚一定的情况下，对连接角度为90°的双弯头进行弯管内径对固有频率影响的分析计算，得到双弯头弯管内径与其固有频率及理论计算得到的弯管谐响应振动幅值的关系，如图8所示。

在理论公式计算中需要利用面积公式将弯管内径的变化转化为横截面积的变化才能进行计算。由图8可看出，在考虑流固耦合的作用时，随着弯管内径的增大弯管的一阶与二阶固有频率呈近似线性增大的趋势，但是其增幅并不完全相同，且二阶固有频率随着弯管内径增大增幅比一阶固有频率增幅较大，即弯管的内径对二阶固有频率的影响比一阶固有频率影响更大。随着管径的增大，压裂弯管越不容易发生失稳现象。且由理论计算得到的弯管谐响应振动幅值曲线可看出，随着弯管内径的增大弯管的谐响应振动幅值呈现类似指数下降的趋势，即随着弯管内径的增大，减振效果也逐渐减弱，由计算结果可看出：在60 MPa压力下，弯管内径在100 mm左右时，振动幅值逐渐趋于平稳，较弯管内径为70 mm时振动幅值减小约20%。

2.3.4 曲率半径对双弯头弯管固有频率的影响

为了分析弯管处的曲率半径对固有频率的影响，分析了弯管内径为70 mm，壁厚为19 mm的双弯管在不同曲率半径下的固有频率，得到弯管的曲率半径对管道前两阶固有频率与谐响应振动幅值的影响曲线（图9）。

图9 双弯头固有频率随弯管曲率半径变化图

由图9可看出，随着弯管曲率半径的增大，双弯管的一阶固有频率减幅较小，基本保持不变，二阶固有频率随曲率半径的增大呈近似非线性减小的趋势，曲率半径超过180 mm以后趋于平缓，而且由图9可看出，随着弯管曲率半径的增大，其振幅明显减小。这是由于流体流过弯头时，由于离心力的作用，压裂液的压力集中在弯管外侧壁附近，随着弯管曲率半径的增大，其压强作用面积也相应增大，而弯管外侧壁压强最大值逐渐减小，且随着曲率半径的增大，形成湍流所需时间增加，弯管受到的不稳定压力增大[14]，因此双弯头弯管的固有频率会逐渐减小，而振幅也会由于最大压强值的减小而逐渐减小[15]。且由理论计算结果可知，谐响应振动幅值随着弯管曲率半径的增大逐渐减小，但减幅较小减小，对管道振动强度的影响不大。

由此可见，弯管的曲率半径是影响压裂管线的固有频率的另一个重要因素。因此对计算结果进行分析可得知，在管汇布局允许的情况下，为了防止弯管振动强度过大，应该在考虑减小弯管的振动强度的同时避开弯管的固有频率，而且为了防止由于弯管曲率半径过小而出现应力集中于弯头凸壁而导致弯头受力不均振幅增大的情况，弯头的曲率半径不宜过大或太小应该尽量控制在160 mm左右。

3 结论

1）在流固耦合作用下，双弯头弯管的连接角度对弯管的稳定性存在较大的影响，压裂现场应该将两个弯头的连接角度尽量控制在75°～105°，弯管的振动强度最大可减小约30%。连接角度太大或太小都会使双弯管固有频率偏低而导致弯管容易在激振力的作用下引起共振。

2）在流固耦合的作用下，双弯头弯管的固有频率随弯管内径的增长呈近似线性增长的关系，压裂现场应尽量选择内径约为101.4 mm左右的压裂管线。

3）双弯头弯管中存在脉动流体时，弯管的曲率半径对双弯头弯管的固有频率与振动幅值都存在较大影响。为使弯管保持稳定，减小管汇的振动强度，在压裂现场激振频率不高的情况下，弯管内径为70 mm时，弯管的曲率半径应该尽量控制在160 mm左右。

[1] Tan JQ, Weniger P, Krooss B, Merkel A, Horsベeld B, Zhang JC,et al. Shale gas potential of the major marine shale formations in the Upper Yangtze Platform, South China, Part II: Methane sorption capacity[J]. Fuel, 2014, 129: 204-218.

[2] Tijsseling AS. Fluid-structure interaction in liquid-ベlled pipe systems: A review[J]. Journal of Fluids and Structures, 1996, 10(2):109-146.

[3] Païdoussis MP & Li GX. Pipes conveying ぼuid: A model dynamical problem[J]. Journal of Fluids and Structures, 1993, 7(2): 137-204.

[4] Tubaldi E, Amabili M & Païdoussis MP. Fluid–structure interaction for nonlinear response of shells conveying pulsatile ぼow[J].Journal of Sound and Vibration, 2016, 371: 252-276.

[5] Ghayesh MH. Parametric vibrations and stability of an axially accelerating string guided by a non-linear elastic foundation[J].International Journal of Non-Linear Mechanics, 2010, 45(4): 382-394.

[6] Ghazali MH, Hee LM & Leong MS. Piping vibration due to pressure pulsations: Review[J]. Advanced Materials Research, 2014,845: 350-354.

[7] 王琳, 倪樵, 黄玉盈. GDQR法用于输流曲管的流致振动研究[J]. 动力学与控制学报, 2005, 3(1): 72-77.Wang Lin, Ni Qiao & Huang Yuying. GDQR for the analyses ofぼow-induced vibrations of curved pipes conveying ぼuid[J]. Journal of Dynamics and Control, 2005, 3(1): 72-77.

[8] Tentarelli SC. Propagation of noise and vibration in complex hydraulic tubing systems[D]. Bethlehem: Lehigh University, 1991.

[9] 李艳华. 考虑流固耦合的管路系统振动噪声及特性研究[D].哈尔滨: 哈尔滨工程大学, 2011.Li Yanhua. Study on vibration and noise and its characteristics of pipeline systems considering ぼuid-structure interaction[D] Harbin: Harbin Engineering University, 2011.

[10] Wang J, Hua H & Gu CS. On the correction of the boundary de-ベciency in SPH for the frictional contact simulation[J]. Science China Technological Sciences, 2014, 57(1): 86-100.

[11] 顾嫒, 郦鸣阳, 沈力行, 喻洪流, 丁皓, 赵改平. 狭窄动脉流固耦合模型ANSYS/CFX数值的有限元分析[J]. 中国组织工程研究与临床康复, 2008, 12(52): 10293-10296.Gu Yuan, Li Mingyang, Shen Lixing, Yu Hongliu, Ding Hao &Zhao Gaiping. Finite element analysis of stenosed artery-blood coupling model in ANSYS/CFX[J]. Journal of Clinical Rehabilitative Tissue Engineering Research, 2008, 12(52): 10293-10296.

[12] Kuehlert K, Webb S, Schowalter D, Holmes W, Chilka A & Reuss S. Simulation of the ぼuid–structure-interaction of steam generator tubes and bluff bodies[J]. Nuclear Engineering and Design, 2008,238(8): 2048-2054.

[13] 付永领, 荆慧强. 弯管转角对液压管道振动特性影响分析[J].振动与冲击, 2013, 32(13): 165-169.Fu Yongling & Jing Huiqiang. Elbow angle effect on hydraulic pipeline vibration characteristics[J]. Journal of Vibration and Shock, 2013, 32(13): 165-169.

[14] Abhari MN, Ghodsian M, Vaghefi M & Panahpur N. Experimental and numerical simulation of ぼow in a 90°bend[J]. Flow Measurement and Instrumentation, 2010, 21(3): 292-298.

[15] Mirzaei M, Najafi M & Niasari H. Experimental and numerical analysis of dynamic rupture of steel pipes under internal high-speed moving pressures[J]. International Journal of Impact Engineering, 2015, 85: 27-36.